Abstract
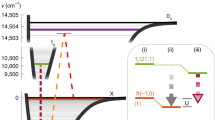
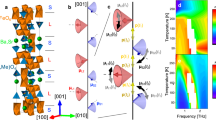
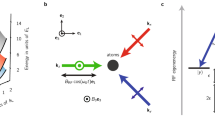
Engineered spin–orbit coupling (SOC) in cold-atom systems can enable the study of new synthetic materials and complex condensed matter phenomena1,2,3,4,5,6,7,8. However, spontaneous emission in alkali-atom spin–orbit-coupled systems is hindered by heating, limiting the observation of many-body effects1,2,5 and motivating research into potential alternatives9,10,11. Here we demonstrate that spin–orbit-coupled fermions can be engineered to occur naturally in a one-dimensional optical lattice clock12. In contrast to previous SOC experiments1,2,3,4,5,6,7,8,9,10,11, here the SOC is both generated and probed using a direct ultra-narrow optical clock transition between two electronic orbital states in 87Sr atoms. We use clock spectroscopy to prepare lattice band populations, internal electronic states and quasi-momenta, and to produce spin–orbit-coupled dynamics. The exceptionally long lifetime of the excited clock state (160 seconds) eliminates decoherence and atom loss from spontaneous emission at all relevant experimental timescales, allowing subsequent momentum- and spin-resolved in situ probing of the SOC band structure and eigenstates. We use these capabilities to study Bloch oscillations, spin–momentum locking and Van Hove singularities in the transition density of states. Our results lay the groundwork for using fermionic optical lattice clocks to probe new phases of matter.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Dalibard, J., Gerbier, F., Juzeliūnas, G. & Öhberg, P. Colloquium: Artificial gauge potentials for neutral atoms. Rev. Mod. Phys. 83, 1523–1543 (2011)
Goldman, N., Juzeliūnas, G., Öhberg, P. & Spielman, I. Light-induced gauge fields for ultracold atoms. Rep. Prog. Phys. 77, 126401 (2014)
Bloch, I., Dalibard, J. & Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 80, 885–964 (2008)
Galitski, V. & Spielman, I. B. Spin–orbit coupling in quantum gases. Nature 494, 49–54 (2013)
Zhai, H. Degenerate quantum gases with spin–orbit coupling: a review. Rep. Prog. Phys. 78, 026001 (2015)
Stuhl, B., Lu, H.-I., Aycock, L., Genkina, D. & Spielman, I. Visualizing edge states with an atomic Bose gas in the quantum Hall regime. Science 349, 1514–1518 (2015)
Mancini, M. et al. Observation of chiral edge states with neutral fermions in synthetic Hall ribbons. Science 349, 1510–1513 (2015)
Atala, M. et al. Observation of chiral currents with ultracold atoms in bosonic ladders. Nat. Phys. 10, 588–593 (2014)
Burdick, N. Q., Tang, Y. & Lev, B. L. Long-lived spin–orbit-coupled degenerate dipolar Fermi gas. Phys. Rev. X 6, 031022 (2016)
Song, B. et al. Spin–orbit coupled two-electron Fermi gases of ytterbium atoms. Preprint at https://arxiv.org/abs/1608.00478 (2016)
Li, J. et al. Spin–orbit coupling and spin textures in optical superlattices. Phys. Rev. Lett. 117, 185301 (2016)
Wall, M. L. et al. Synthetic spin–orbit coupling in an optical lattice clock. Phys. Rev. Lett. 116, 035301 (2016)
Bloom, B. J. et al. An optical lattice clock with accuracy and stability at the 10−18 level. Nature 506, 71–75 (2014)
Hügel, D. & Paredes, B. Chiral ladders and the edges of quantum Hall insulators. Phys. Rev. A 89, 023619 (2014)
Aidelsburger, M. et al. Realization of the Hofstadter Hamiltonian with ultracold atoms in optical lattices. Phys. Rev. Lett. 111, 185301 (2013)
Miyake, H., Siviloglou, G. A., Kennedy, C. J., Burton, W. C. & Ketterle, W. Realizing the Harper Hamiltonian with laser-assisted tunneling in optical lattices. Phys. Rev. Lett. 111, 185302 (2013)
Celi, A. et al. Synthetic gauge fields in synthetic dimensions. Phys. Rev. Lett. 112, 043001 (2014)
Barbarino, S., Taddia, L., Rossini, D., Mazza, L. & Fazio, R. Magnetic crystals and helical liquids in alkaline-earth fermionic gases. Nat. Commun. 6, 8134 (2015)
Martin, M. J. et al. A quantum many-body spin system in an optical lattice clock. Science 341, 632–636 (2013)
Blatt, S. et al. Rabi spectroscopy and excitation inhomogeneity in a one-dimensional optical lattice clock. Phys. Rev. A 80, 052703 (2009)
Lemonde, P. & Wolf, P. Optical lattice clock with atoms confined in a shallow trap. Phys. Rev. A 72, 033409 (2005)
Van Hove, L. The occurrence of singularities in the elastic frequency distribution of a crystal. Phys. Rev. 89, 1189–1193 (1953)
Kim, P., Odom, T. W., Huang, J.-L. & Lieber, C. M. Electronic density of states of atomically resolved single-walled carbon nanotubes: Van Hove singularities and end states. Phys. Rev. Lett. 82, 1225–1228 (1999)
Ben Dahan, M., Peik, E., Reichel, J., Castin, Y. & Salomon, C. Bloch oscillations of atoms in an optical potential. Phys. Rev. Lett. 76, 4508–4511 (1996)
Preiss, P. M. et al. Strongly correlated quantum walks in optical lattices. Science 347, 1229–1233 (2015)
Isaev, L., Schachenmayer, J. & Rey, A. Spin–orbit-coupled correlated metal phase in Kondo lattices: an implementation with alkaline-earth atoms. Phys. Rev. Lett. 117, 135302 (2016)
Zhang, X. et al. Spectroscopic observation of SU(N)-symmetric interactions in Sr orbital magnetism. Science 345, 1467–1473 (2014)
Livi, L. F. et al. Synthetic dimensions and spin–orbit coupling with an optical clock transition. Phys. Rev. Lett. 117, 220401 (2016)
An, F. A., Meier, E. J. & Gadway, B. Direct observation of chiral currents and magnetic reflection in atomic flux lattices. Preprint at https://arxiv.org/abs/1609.09467 (2016)
Lignier, H. et al. Dynamical control of matter-wave tunnelling in periodic potentials. Phys. Rev. Lett. 99, 220403 (2007)
Parker, C. V., Ha, L.-C. & Chin, C. Direct observation of effective ferromagnetic domains of cold atoms in a shaken optical lattice. Nat. Phys. 9, 769–774 (2013)
Jotzu, G. et al. Experimental realization of the topological Haldane model with ultracold fermions. Nature 515, 237–240 (2014)
Fläschner, N. et al. Experimental reconstruction of the Berry curvature in a Floquet Bloch band. Science 352, 1091–1094 (2016)
Müller, T., Fölling, S., Widera, A. & Bloch, I. State preparation and dynamics of ultracold atoms in higher lattice orbitals. Phys. Rev. Lett. 99, 200405 (2007)
Spielman, I. B. et al. Collisional deexcitation in a quasi-two-dimensional degenerate bosonic gas. Phys. Rev. A 73, 020702 (2006)
Bishof, M. et al. Inelastic collisions and density-dependent excitation suppression in a 87Sr optical lattice clock. Phys. Rev. A 84, 052716 (2011)
Martin, M. J. Quantum Metrology and Many-body Physics: Pushing the Frontier of the Optical Lattice Clock. PhD thesis, Univ. Colorado, Boulder (2013)
Wall, M. L., Hazzard, K. R. A. & Rey, A. M. Effective many-body parameters for atoms in nonseperable Gaussian optical potentials. Phys. Rev. A 92, 013610 (2015)
Acknowledgements
We are grateful to N. R. Cooper for insights and discussions, and S. L. Campbell, N. Darkwah Oppong, A. Goban, R. B. Hutson, D. X. Reed, J. Robinson, L. Sonderhouse and W. Zhang for technical contributions and discussions. This research is supported by NIST, the NSF Physics Frontier Center at JILA (NSF-PFC-1125844), AFOSR-MURI, AFOSR, DARPA and ARO. S.K., M.L.W. and G.E.M. acknowledge the NRC postdoctoral fellowship programme.
Author information
Authors and Affiliations
Contributions
S.K., S.L.B., T.B., G.E.M., X.Z. and J.Y. contributed to the experiments. M.L.W., A.P.K. and A.M.R. contributed to the development of the theoretical model. All authors discussed the results, contributed to the data analysis and worked together on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Reviewer Information
Nature thanks L. Duan and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Extended data figures and tables
Extended Data Figure 1 Bloch band preparation and spectroscopy.
a, Spectroscopy of atoms prepared in |g〉0 reveals the band spacing of the lattice, with inter-band transitions colour-coded by the final band. b, Spectroscopy of atoms in |e〉1, prepared by driving the |g〉0 → |e〉1 transition shown in a and then removing any remaining atoms in |g〉. The spectrum for atoms in |e〉0 from Fig. 1d is shown for comparison (dashed grey line).
Extended Data Figure 2 Rabi line shape modelling.
a–e, Theoretical modelling of carrier line shapes starting from the |g〉0 (a–c) or |e〉1 (d, e) state. For the ground band transitions (a–c), all data were taken using a π pulse, and are well reproduced by a perturbative model (solid lines). Three specific cases are shown covering from the deep-lattice regime (Uz ≈ 65Er; a) to the moderate-lattice regime (Uz ≈ 10Er; b), and down to the shallow-lattice limit (Uz ≈ 3Er; c). For the first excited band transitions, the data in the deeper-lattice case (Uz ≈ 21.3Er), taken with a π pulse, are well reproduced by the perturbative model (d). However, for the case of Uz ≈ 16Er where a longer pulse was used, the perturbative theory, which ignores radial sideband transitions induced by the laser, captures only the width of the line shape and not its amplitude (e).
Extended Data Figure 3 Modelling of quasi-momentum selection.
Theoretical probability distribution P(q, nr) of quasi-momentum and radial quantum number nr of |e〉 excitations resulting from exciting a thermal distribution in |g〉 with a 50-ms π pulse. The lattice depth is Uz ≈ 16Er, resulting in a tunnelling rate of J ≈ 17 Hz. The distribution of atoms among q is broadened owing to the fact that the Rabi frequency and tunnelling rates are comparable, but can be made narrower by decreasing the Rabi frequency.
Rights and permissions
About this article
Cite this article
Kolkowitz, S., Bromley, S., Bothwell, T. et al. Spin–orbit-coupled fermions in an optical lattice clock. Nature 542, 66–70 (2017). https://doi.org/10.1038/nature20811
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature20811
This article is cited by
-
Strongly interacting Rydberg atoms in synthetic dimensions with a magnetic flux
Nature Communications (2024)
-
Synthetic dimensions for topological and quantum phases
Communications Physics (2024)
-
Spin-orbit Rabi oscillations in optically synthesized magnetic fields
Light: Science & Applications (2023)
-
Observation of frustrated chiral dynamics in an interacting triangular flux ladder
Nature Communications (2023)
-
Thouless pumping and topology
Nature Reviews Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.