Abstract
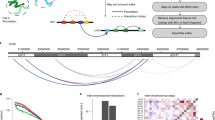
Chromosomes are folded into highly compacted structures to accommodate physical constraints within nuclei and to regulate access to genomic information1,2. Recently, global mapping of pairwise contacts showed that loops anchoring topological domains (TADs) are highly conserved between cell types and species3,4,5,6,7,8. Whether pairwise loops9,10,11,12,13,14 synergize to form higher-order structures is still unclear. Here we develop a conformation capture assay to study higher-order organization using chromosomal walks (C-walks) that link multiple genomic loci together into proximity chains in human and mouse cells. This approach captures chromosomal structure at varying scales. Inter-chromosomal contacts constitute only 7–10% of the pairs and are restricted by interfacing TADs. About half of the C-walks stay within one chromosome, and almost half of those are restricted to intra-TAD spaces. C-walks that couple 2–4 TADs indicate stochastic associations between transcriptionally active, early replicating loci. Targeted analysis of thousands of 3-walks anchored at highly expressed genes support pairwise, rather than hub-like, chromosomal topology at active loci. Polycomb-repressed Hox domains are shown by the same approach to enrich for synergistic hubs. Together, the data indicate that chromosomal territories, TADs, and intra-TAD loops are primarily driven by nested, possibly dynamic, pairwise contacts.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Cremer, T. & Cremer, M. Chromosome territories. Cold Spring Harb. Perspect. Biol . 2, a003889 (2010)
Dekker, J., Marti-Renom, M. A. & Mirny, L. A. Exploring the three-dimensional organization of genomes: interpreting chromatin interaction data. Nature Rev. Genet. 14, 390–403 (2013)
Dixon, J. R. et al. Chromatin architecture reorganization during stem cell differentiation. Nature 518, 331–336 (2015)
Nagano, T. et al. Single-cell Hi-C reveals cell-to-cell variability in chromosome structure. Nature 502, 59–64 (2013)
Vietri Rudan, M. et al. Comparative Hi-C reveals that CTCF underlies evolution of chromosomal domain architecture. Cell Reports 10, 1297–1309 (2015)
Dixon, J. R. et al. Topological domains in mammalian genomes identified by analysis of chromatin interactions. Nature 485, 376–380 (2012)
Sexton, T. et al. Three-dimensional folding and functional organization principles of the Drosophila genome. Cell 148, 458–472 (2012)
Nora, E. P. et al. Spatial partitioning of the regulatory landscape of the X-inactivation centre. Nature 485, 381–385 (2012)
Zuin, J. et al. Cohesin and CTCF differentially affect chromatin architecture and gene expression in human cells. Proc. Natl Acad. Sci. USA 111, 996–1001 (2014)
Sofueva, S. et al. Cohesin-mediated interactions organize chromosomal domain architecture. EMBO J . 32, 3119–3129 (2013)
Rao, S. S. P. et al. A 3D map of the human genome at kilobase resolution reveals principles of chromatin looping. Cell 159, 1665–1680 (2014)
Zhang, Y. et al. Chromatin connectivity maps reveal dynamic promoter–enhancer long-range associations. Nature 504, 306–310 (2013)
Phillips-Cremins, J. E. et al. Architectural protein subclasses shape 3D organization of genomes during lineage commitment. Cell 153, 1281–1295 (2013)
Tang, Z. et al. CTCF-mediated human 3D genome architecture reveals chromatin topology for transcription. Cell 163, 1611–1627 (2015)
Nagano, T. et al. Comparison of Hi-C results using in-solution versus in-nucleus ligation. Genome Biol. 16, 175 (2015)
Ay, F. et al. Identifying multi-locus chromatin contacts in human cells using tethered multiple 3C. BMC Genomics 16, 121 (2015)
Andrey, G. et al. A switch between topological domains underlies HoxD genes collinearity in mouse limbs. Science 340, 1234167 (2013)
Fudenberg, G. et al. Formation of chromosomal domains by loop extrusion. Cell Reports 15, 2038–2049 (2016)
Sanborn, A. L. et al. Chromatin extrusion explains key features of loop and domain formation in wild-type and engineered genomes. Proc. Natl Acad. Sci. USA 112, E6456–E6465 (2015)
Cheutin, T. & Cavalli, G. Polycomb silencing: from linear chromatin domains to 3D chromosome folding. Curr. Opin. Genet. Dev. 25, 30–37 (2014)
Schuettengruber, B. et al. Cooperativity, specificity, and evolutionary stability of Polycomb targeting in Drosophila. Cell Reports 9, 219–233 (2014)
Fabre, P. J. et al. Nanoscale spatial organization of the HoxD gene cluster in distinct transcriptional states. Proc. Natl Acad. Sci. USA 112, 13964–13969 (2015)
Boettiger, A. N. et al. Super-resolution imaging reveals distinct chromatin folding for different epigenetic states. Nature 529, 418–422 (2016)
Engreitz, J. M. et al. The Xist lncRNA exploits three-dimensional genome architecture to spread across the X chromosome. Science 341, 1237973 (2013)
Williamson, I. et al. Spatial genome organization: contrasting views from chromosome conformation capture and fluorescence in situ hybridization. Genes Dev. 28, 2778–2791 (2014)
Imakaev, M. V., Fudenberg, G. & Mirny, L. A. Modeling chromosomes: Beyond pretty pictures. FEBS Lett . 589, 3031–3036 (2015)
Giorgetti, L. et al. Predictive polymer modeling reveals coupled fluctuations in chromosome conformation and transcription. Cell 157, 950–963 (2014)
Geula, S. et al. m6A mRNA methylation facilitates resolution of naïve pluripotency toward differentiation. Science 347, 1002–1006 (2015)
Schwartzman, O. et al. UMI-4C for quantitative and targeted chromosomal contact profiling. Nature Methods 13, 685–691 (2016)
Ryba, T., Battaglia, D., Pope, B. D., Hiratani, I. & Gilbert, D. M. Genome-scale analysis of replication timing: from bench to bioinformatics. Nature Protocols 6, 870–895 (2011)
Hansen, R. S. et al. Sequencing newly replicated DNA reveals widespread plasticity in human replication timing. Proc. Natl Acad. Sci. USA 107, 139–144 (2010)
Splinter, E. et al. CTCF mediates long-range chromatin looping and local histone modification in the β-globin locus. Genes Dev. 20, 2349–2354 (2006)
Deng, W. et al. Reactivation of developmentally silenced globin genes by forced chromatin looping. Cell 158, 849–860 (2014)
Acknowledgements
We acknowledge E. Yaffe for help with early stages of the experiments, N. Mor for help with mES cells, and members of the A.T. group for discussions. Research at the A.T. group was supported by the European Research Council (EVOEPIC), Flight Attendant Medical Research Institute (FAMRI), and the Israel Science Foundation (ISF). A.T. is a Kimmel investigator.
Author information
Authors and Affiliations
Contributions
P.O.-C. and A.T. designed the study with help from Z.M. P.O.-C. and Z.M. developed and optimized the experimental approach with help from N.O.E., O.S. and Y.L. P.O.-C. and A.T. developed the algorithmic approaches and analysed the data, with help from A.L., Y.L. and O.S. G.D. and R.B.P. performed PacBio sequencing. P.O.-C. and A.T. wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
Extended Data Figure 1 C-walk profiling.
a, Log probability of contact as a function of log linear genomic distance, shown based on data from C-walks of length 2,3,4 and longer than 4. When quantifying pairwise contact probability from a C-walk, all hops are considered. b, Similar to a, but showing contact probability for logarithmic bins (without dividing by bin size). Overall these data show that contacts occur with probabilities that have a similar scale for close, medium and far ranges. However, the intra-domain distance range contacts (<1 Mb) are enriched 2–3 fold above the 10 Mb distance range. c, Distribution of the number of hops derived when analysing linear genomic DNA using the full C-walk protocol. d, Bar graph depicts the probability of C-walks (of increasing length) derived from linear genomic DNA to jump over 0, 1 and up to 20 and above DpnII restriction fragments. We note that some jumps occur due to short fragment sizes, and other due to imperfect amplification and sequencing. e, The probability of inferring a long hop (over 50 fragments) in linear genomic DNA C-walks. This provides estimation on the total level of noise (cross C-walk contamination) expected when preforming C-walk analysis on 3C DNA. f, Cross-species controls. Human- and mouse-derived 3C material was mixed and processed together to measure the level of cross-C-walk contamination using 3C template instead of genomic DNA. Reads were mapped to a hybrid genome comprising the hg19 assembly appended by the mm9 assembly. The levels of reads that mapped to both genomes is minute and comparable to the levels found when mapping human-only and mouse-only C-walks to the hybrid assembly confirming the fact that C-walk cross contamination is not a major source of noise in the shotgun approach. g, We used C-walks from class II with four or more hops (left) and C-walks from class III (right), to extract all inter-chromosomal hops and reconstruct a chromosome-to-chromosome contact matrix. We compute the expected number of pairwise chromosomal contacts for each pair by multiplying the total number of inter-chromosomal contacts for the two chromosomes and scaling to the sum of observed contacts. Shown are colour-coded enrichment (log(observed/expected)) values for each chromosome pair, indicating, for example, a clear t(9;22) signature (as expected in K562) in class II data. Class III C-walks recreate a nearly random contact preference among all chromosomes. The residual signal in the class III matrix suggests a low rate of non-spurious hops that are misclassified as class III C-walks. h, The cumulative distributions of the log(enrichment) ratios for both classes is also shown.
Extended Data Figure 2 Hi-C and TAD inference.
a, We performed 4-cutter Hi-C in mES cells, generating 145 million distinct contacts. Shown are large-scale Hi-C maps derived from this data. b, Genome-wide distribution of insulation intensities in mES and K562 cells, using a 200 kb scale (Methods; computed as described previously10). The threshold values we used in order to demarcate TADs are marked as vertical lines. c, Overlay of the analogue insulation intensity level on a region of chromosome 5 in mES cells, illustrating TAD calling. Our analysis suggests that there is no single canonical definition of TADs, since loops occur at several scales, but the threshold we select is providing a good reference scale that demarcate TADs with typical sizes of 1–2 Mb. d, Distributions of TAD sizes. e, Distribution of the number of inter-chromosomal traversals for class II C-walks. f, We classified all class II C-walks with two or more inter-chromosomal-traversing contacts into five subclasses determined by the properties of the two contacting elements on both chromosomes (‘point’, both contacts are contained within a 1 kb range; ‘TAD’, restricted to one TAD; ‘territory’, spanning more than one TAD). We found that only a small fraction (<3%) of the interfaces coupled the two chromosomes through contacts between multiple TADs at both chromosomes. On the other hand, most interfaces either linked the chromosomes through two contacting TADs (grey and blue), or associated one TAD in one chromosome with elements from more than one TAD in the other chromosome. Data from simulated, pairwise independent C-walks are provided for control. g, Fraction of intra-chromosomal ligations, distribution of the number of chromosomes visited and the size of inter-chromosomal interface for simulated, pairwise independent C-walks.
Extended Data Figure 3 TAD inference statistics and C-walks derived by PacBio sequencing.
a, Distributions of mean time of replication (ToR) across TADs. Note that normalization of ToR in mES30 and K562 cells31 is different. b, Correspondence between ToR and mean enrichment of H3K4me3 on transcription start sites (TSSs). c, Distribution of TAD sizes, shown separately for the active and inactive classes. d, Probability of pairwise inter-chromosomal hops in C-walks (excluding class III), estimated separately from inactive (left) and active (right) source loci (regardless of the TAD type at the target locus). e, For each class II C-walk we counted the number and types (active/inactive) of TADs visited on each of the two chromosomes. The bar graphs summarize these statistics separately for walks visiting one TAD on each chromosome (top left), one TAD in one chromosome and two in the other (right), and two TADs on each chromosome (which are rare as suggested by the data in Extended Data Fig. 2f). Each bar shows the breakdown of the number of active TADs visited in the second chromosome, conditioned on the number of active TADs visited in the first chromosome. P values are based on a chi-squared test, showing that composition of TAD types in the inter-chromosomal interfaces is non-random and prefers association of multiple active TADs or multiple inactive TADs. f, Shown are the 5–95% span quantiles (in steps of 10%) for C-walks with increasing number of hops (linear scale, top; log scale, bottom). g, Comparison of C-walks derived from our shotgun sequencing procedure (indirect) versus direct PacBio sequencing (direct). Statistics on the probability of pairwise contact given genomic distance (left), and the span of C-walks on four hops (right) corroborate the integrity of our C-walk assembly process. Note data are shown for both K562 and mES cells. h, Distributions of spans for observed and simulated C-walks in active (top) and inactive (bottom) TAD contexts.
Extended Data Figure 4 C-walk span supporting statistics and C-walk results on mES cells.
a, b, Shown are cumulative distributions of the relative span (C-walk span divided by TAD size), for intra-TAD C-walks of increasing length (left to right), classified based on the type of TAD (active and inactive). Data are shown for TADs of two size ranges with sufficient statistics. P values are based on a Kolmogorov–Smirnov test. This supports Fig. 2g. c–g, Similar to Fig. 2d–g, j but using mES cells data. h, C-walks of more than three hops can be characterized as pairwise when they visit two chromosomal neighbourhoods but not any position in between them. Quantitatively, we define the tri-distance of a C-walk as the maximal distance of any hop from the minimum and maximum positions of the walk and analyse the distributions of the ratios between tri-distance and span for C-walks of six hops and more. Low ratios indicate a pairwise interface, while ratios around 0.5 represent maximally non-pairwise structure. We observed that high-span C-walks are enriched for cases with tri-distance to span ratio of 0.1 and less. On the other hand, C-walks with shorter spans (for example, less than 1 Mb) usually do not show up as strongly pairwise, possibly since the sensitivity of 3C is limited for short-range contacts. i, Shown are cumulative distributions of observed and simulated tri-diff scores on C-walks stratified by span (from 2 Mb to 32 Mb). P values are based on Kolmogorov–Smirnov statistics. j, Heatmaps representing the distribution of tri-distance scores for C-walks stratified by span.
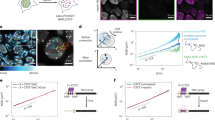
Extended Data Figure 5 3way-4C analysis.
a, 3-Walk generation scheme. A first hop from the bait V to X is sampled from the pairwise chromosomal neighbourhood around V. This hop indicates that the neighbourhoods of V and X are now physically coupled. The second hop can therefore be sampled from either V (right) or X (left) pairwise neighbourhoods. The sampling ratio between the two neighbourhoods is determined from C-walk data. Note that if (V,X,Y) is a true synergistic hub, the probability of observing it should be higher than predicted by such independent sampling of pairs (V,X), (V,Y) and (X,Y). b, Analysis procedure. The input (right) is a set of 3-walks originating from the viewpoint bait V summarized in a matrix (X,Y). Simulated (X,Y) triplets (left) are generated by sampling from the pairwise chromosomal neighbourhood as outlined in a (see Methods for complete details). To compare the observed and simulated triplet distributions, we compute for any observed triplet (V–X–Y), the K nearest observed contacts (in Euclidean space), and K′ (K scaled by the size of the sample) nearest simulated contacts. Comparison is done using Kolmogorov–Smirnov D statistics on the cumulative distributions of distances. If distances are significantly shorter in the observed data (distributions II), we annotate the triplet as synergistic (colour-coded red–yellow). If the distances are significantly shorter in the randomized data (distributions I), we annotate the triplet as insulated (colour-coded blue). c, Comparing score distribution on observed and simulated data. Shown are empirical cumulative density functions for positive (right) and negative (left) D statistics using data from the EIF1B locus (Fig. 3b). Colour coding is the same as the one used in the visualization of triplet matrices. d, We defined the background range for each point in the EIF1B data set as the 0.1 quantile in the K′ nearest neighbour within the simulated data set. We compute the fraction of contacts in the observed K nearest neighbour that are within this range, and derive an enrichment ratio by dividing the observed fraction by the background fraction (0.1). Shown is a comparison of the D score and the enrichment ratio (note the y axis is in log scale). We note that setting the background level at 10% is not always appropriate, so we use the D score (which is not pre-defining a background level) directly for visualization. e, Comparing D scores for replicate experiments in the EIF1B locus. f, Interpretation. Points with similar observed and simulated statistics (annotated as grey in the matrix), represent cases where pairwise 3C is predicting the behaviour of 3-walks. We note that this can be a consequence of limited 3C resolution. It can also suggest that within individual nuclei the contacts V,X and V,Y are indeed occurring independently. When enrichment is observed, we can classify it into at least three types. Cases in which enriched triplets are bringing together two loci that are either linked with each other (class 1), or linked on one end to the viewpoint (class 2), can be interpreted as a pairwise contact with specific additional local structure (for example, see Fig. 3c), or as restricting contact with additional loci given an existing pairwise contact. Note that in any case, the analysis excludes contacts that occur within less than 3 kb, so such local structure should be understood on a scale of few kilobases. Only when the hotspot involves three distinct loci can we hypothesize that a true long-range hub is observed (class 3). In addition, 3-walk distribution can also identify insulation between X and Y, which can be observed when interrogating from within the insulated loops (class 4) or outside of these (class 5).
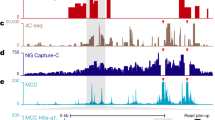
Extended Data Figure 6 Hi-C and 3way-4C analyses for the GATA2, GATA1 and FTL loci.
a, Hi-C maps showing contact structure at the GATA2 regions. The locus is flanked by two loops (H1 and H2), and these are shown by Hi-C to be frequently fused to form a bigger loop (H3). b, Hi-C and 3way-4C analysis at the GATA1 locus. Note that this gene-dense region is qualitatively different from the GATA2 or EIF1B loci, and is characterized by complex pairwise contact landscapes as shown by Hi-C. This suggests potential enrichment of many enhancer- or promoter-synergistic hubs. Nevertheless, the data suggest tri-way contacts are predicted by pairwise contact distributions around this region. c, Bar graphs show observed and expected triplet contacts for H3 loops on EIF1B1 and GATA2 loci, supporting a lack of synergistic hub enrichment. d, Hi-C and 3way-4C analyses for the FTL locus. FTL is highly expressed in K562 cells, and is located in a region with many additional active genes. Multiple long-range contacts are observed in pairwise Hi-C analysis of this region. 3way-4C enrichment maps show that the pairwise models are generally consistent with the data, with some enrichment for contacts bringing together the BCAT2-HSD17B14 locus with the encapsulating CTCF loop (v1).
Extended Data Figure 7 Hi-C and 3way-4C analyses for the ANK1 locus.
Similar to Fig. 3a, b. A complex contact structure around the ANK1 locus is depicted by Hi-C analysis. 3way-4C on two baits suggests possible extended pairwise contact with the expressed ANK1 and KAT6A loci, but offers no support for long-range synergistic tri-way hubs.
Extended Data Figure 8 Hi-C and 3way-4C analyses for the β-globin cluster.
Similar to Fig. 3a, b. Multiple strong loops32,33 are shown by Hi-C, marked H1 to H7. 3-Walk distribution suggests enrichment of multi-contacts between the locus control region (LCR) and the globin genes from the v4, v5 and v6 viewpoints (located at or near the LCR). In addition, the olfactory receptor (OR) cluster upstream the globin cluster shows weak expression (marked pink) as well as involvement in pairwise contacts with baits within the LCR and downstream of it. This may suggest enrichment of local contacts between the β-globin regulatory machinery and that sites within this cluster are involved in invasion of gene expression into this repressed TAD.
Extended Data Figure 10 Hi-C and 3way-4C analyses for the Hoxc and Hoxb cluster in mES cells.
Annotation is as described for Fig. 4a.
Supplementary information
Supplementary Table 1
This file contains the C-Walk statistics. (XLSX 29 kb)
Supplementary Table 2
This file contains the 3way-4C bait data base. (XLSX 15 kb)
Supplementary Table 3
This file contains a list of epigenomic data sets used. (XLSX 8 kb)
Rights and permissions
About this article
Cite this article
Olivares-Chauvet, P., Mukamel, Z., Lifshitz, A. et al. Capturing pairwise and multi-way chromosomal conformations using chromosomal walks. Nature 540, 296–300 (2016). https://doi.org/10.1038/nature20158
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature20158
This article is cited by
-
Single cell Hi-C identifies plastic chromosome conformations underlying the gastrulation enhancer landscape
Nature Communications (2023)
-
Multiplex-GAM: genome-wide identification of chromatin contacts yields insights overlooked by Hi-C
Nature Methods (2023)
-
The Nodewalk assay to quantitate chromatin fiber interactomes in very small cell populations
Nature Protocols (2023)
-
Dynamic 3D genome architecture of cotton fiber reveals subgenome-coordinated chromatin topology for 4-staged single-cell differentiation
Genome Biology (2022)
-
Deciphering multi-way interactions in the human genome
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.