Abstract
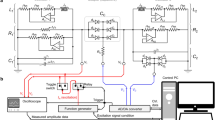
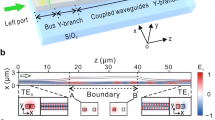
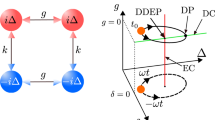
Physical systems with loss or gain have resonant modes that decay or grow exponentially with time. Whenever two such modes coalesce both in their resonant frequency and their rate of decay or growth, an ‘exceptional point’ occurs, giving rise to fascinating phenomena that defy our physical intuition1,2,3,4,5,6. Particularly intriguing behaviour is predicted to appear when an exceptional point is encircled sufficiently slowly7,8, such as a state-flip or the accumulation of a geometric phase9,10. The topological structure of exceptional points has been experimentally explored11,12,13, but a full dynamical encircling of such a point and the associated breakdown of adiabaticity14,15,16,17,18,19,20,21 have remained out of reach of measurement. Here we demonstrate that a dynamical encircling of an exceptional point is analogous to the scattering through a two-mode waveguide with suitably designed boundaries and losses. We present experimental results from a corresponding waveguide structure that steers incoming waves around an exceptional point during the transmission process. In this way, mode transitions are induced that transform this device into a robust and asymmetric switch between different waveguide modes. This work will enable the exploration of exceptional point physics in system control and state transfer schemes at the crossroads between fundamental research and practical applications.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Berry, M. V. Physics of nonhermitian degeneracies. Czech. J. Phys. 54, 1039–1047 (2004)
Bender, C. M. Making sense of non-Hermitian Hamiltonians. Rep. Prog. Phys. 70, 947 (2007)
Rotter, I. A non-Hermitian Hamilton operator and the physics of open quantum systems. J. Phys. A 42, 153001 (2009)
Moiseyev, N. Non-Hermitian Quantum Mechanics (Cambridge Univ. Press, 2011)
Heiss, W. D. The physics of exceptional points. J. Phys. A 45, 444016 (2012)
Cao, H. & Wiersig, J. Dielectric microcavities: model systems for wave chaos and non-Hermitian physics. Rev. Mod. Phys. 87, 61–111 (2015)
Lefebvre, R., Atabek, O., Šindelka, M. & Moiseyev, N. Resonance coalescence in molecular photodissociation. Phys. Rev. Lett. 103, 123003 (2009)
Atabek, O. et al. Proposal for a laser control of vibrational cooling in Na2 using resonance coalescence. Phys. Rev. Lett. 106, 173002 (2011)
Latinne, O. et al. Laser-induced degeneracies involving autoionizing states in complex atoms. Phys. Rev. Lett. 74, 46–49 (1995)
Mailybaev, A. A., Kirillov, O. N. & Seyranian, A. P. Geometric phase around exceptional points. Phys. Rev. A 72, 014104 (2005)
Dembowski, C. et al. Experimental observation of the topological structure of exceptional points. Phys. Rev. Lett. 86, 787–790 (2001)
Lee, S.-B. et al. Observation of an exceptional point in a chaotic optical microcavity. Phys. Rev. Lett. 103, 134101 (2009)
Gao, T. et al. Observation of non-Hermitian degeneracies in a chaotic exciton-polariton billiard. Nature 526, 554–558 (2015)
Uzdin, R., Mailybaev, A. & Moiseyev, N. On the observability and asymmetry of adiabatic state flips generated by exceptional points. J. Phys. A 44, 435302 (2011)
Berry, M. V. Optical polarization evolution near a non-Hermitian degeneracy. J. Opt. 13, 115701 (2011)
Berry, M. V. & Uzdin, R. Slow non-Hermitian cycling: exact solutions and the Stokes phenomenon. J. Phys. A 44, 435303 (2011)
Demange, G. & Graefe, E.-M. Signatures of three coalescing eigenfunctions. J. Phys. A 45, 025303 (2012)
Gilary, I., Mailybaev, A. A. & Moiseyev, N. Time-asymmetric quantum-state-exchange mechanism. Phys. Rev. A 88, 010102 (2013)
Graefe, E.-M., Mailybaev, A. A. & Moiseyev, N. Breakdown of adiabatic transfer of light in waveguides in the presence of absorption. Phys. Rev. A 88, 033842 (2013)
Kaprálová-Žd’ánská, P. R. & Moiseyev, N. Helium in chirped laser fields as a time-asymmetric atomic switch. J. Chem. Phys. 141, 014307 (2014)
Milburn, T. J. et al. General description of quasiadiabatic dynamical phenomena near exceptional points. Phys. Rev. A 92, 052124 (2015)
Lin, Z. et al. Unidirectional invisibility induced by PT-symmetric periodic structures. Phys. Rev. Lett. 106, 213901 (2011)
Regensburger, A. et al. Parity–time synthetic photonic lattices. Nature 488, 167–171 (2012)
Feng, L. et al. Experimental demonstration of a unidirectional reflectionless parity-time metamaterial at optical frequencies. Nat. Mater. 12, 108–113 (2012)
Liertzer, M. et al. Pump-induced exceptional points in lasers. Phys. Rev. Lett. 108, 173901 (2012)
Brandstetter, M. et al. Reversing the pump dependence of a laser at an exceptional point. Nat. Commun. 5, 4034 (2014)
Peng, B. et al. Loss-induced suppression and revival of lasing. Science 346, 328–332 (2014)
Hodaei, H., Miri, M.-A., Heinrich, M., Christodoulides, D. N. & Khajavikhan, M. Parity-time–symmetric microring lasers. Science 346, 975–978 (2014)
Feng, L., Wong, Z. J., Ma, R.-M., Wang, Y. & Zhang, X. Single-mode laser by parity-time symmetry breaking. Science 346, 972–975 (2014)
Peng, B. et al. Chiral modes and directional lasing at exceptional points. Proc. Natl Acad. Sci. 113, 6845–6850 (2016)
Xu, H., Mason, D., Jiang, L. & Harris, J. G. E. Topological energy transfer in an optomechanical system with exceptional points. Nature http://www.dx.doi.org/10.1038/nature18604 (2016)
Libisch, F., Rotter, S. & Burgdörfer, J. Coherent transport through graphene nanoribbons in the presence of edge disorder. New J. Phys. 14, 123006 (2012)
Dietz, O., Kuhl, U., Stöckmann, H.-J., Makarov, N. M. & Izrailev, F. M. Microwave realization of quasi-one-dimensional systems with correlated disorder. Phys. Rev. B 83, 134203 (2011)
Acknowledgements
J.D., A.G. and S.R. are supported by the Austrian Science Fund (FWF) through project numbers SFB IR-ON F25-14, SFB-NextLite F49-P10 and I 1142- N27 (GePartWave). The computational results presented were achieved in part using the Vienna Scientific Cluster. A.A.M. is supported by the National Council for Scientific and Technological Development (CNPq) grant number 302351/2015-9 and by the FAPERJ grant number E-26/210.874/2014. J.B. and U.K. acknowledge ANR project number I 1142-N27 (GePartWave). F.L. acknowledges support by the FWF through SFB-F41 VI-COM. T.J.M. and P.R. are supported by the FWF through DK CoQuS W 1210, SFB FOQUS F40, START (grant number Y 591-N16), and project OPSOQI (316607) of the WWTF. N.M. acknowledges I-Core (the Israeli Excellence Center ‘Circle of Light’) and the Israel Science Foundation (grant numbers 298/11 and 1530/15) for their financial support.
Author information
Authors and Affiliations
Contributions
J.D., A.A.M., A.G., F.L., T.J.M., P.R., N.M., and S.R. developed the theoretical framework and performed numerical simulations. J.B., J.D. and U.K. designed the experiment. J.B. and U.K. were responsible for the experimental implementation, the data acquisition and its evaluation. All authors contributed to the analysis, interpretation and discussion of the theoretical and experimental findings, as well as to the preparation of the manuscript. The project was jointly supervised by A.A.M. and S.R. (theory) and by U.K. (experiment).
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
This file contains Supplementary Methods, Supplementary Figures 1-12 and Supplementary References. (PDF 965 kb)
Rights and permissions
About this article
Cite this article
Doppler, J., Mailybaev, A., Böhm, J. et al. Dynamically encircling an exceptional point for asymmetric mode switching. Nature 537, 76–79 (2016). https://doi.org/10.1038/nature18605
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature18605
This article is cited by
-
Chiral transmission by an open evolution trajectory in a non-Hermitian system
Light: Science & Applications (2024)
-
Non-hermiticity in spintronics: oscillation death in coupled spintronic nano-oscillators through emerging exceptional points
Nature Communications (2024)
-
Creating pairs of exceptional points for arbitrary polarization control: asymmetric vectorial wavefront modulation
Nature Communications (2024)
-
Exceptional dynamics at exceptional points
Light: Science & Applications (2024)
-
Chiral exceptional point and coherent suppression of backscattering in silicon microring with low loss Mie scatterer
eLight (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.