Abstract
Topological operations can achieve certain goals without requiring accurate control over local operational details; for example, they have been used to control geometric phases and have been proposed as a way of controlling the state of certain systems within their degenerate subspaces1,2,3,4,5,6,7,8. More recently, it was predicted that topological operations can be used to transfer energy between normal modes, provided that the system possesses a specific type of degeneracy known as an exceptional point9,10,11. Here we demonstrate the transfer of energy between two vibrational modes of a cryogenic optomechanical device using topological operations. We show that this transfer arises from the presence of an exceptional point in the spectrum of the device. We also show that this transfer is non-reciprocal12,13,14. These results open up new directions in system control; they also open up the possibility of exploring other dynamical effects related to exceptional points15,16, including the behaviour of thermal and quantum fluctuations in their vicinity.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Simon, B. Holonomy, the quantum adiabatic theorem, and Berry’s phase. Phys. Rev. Lett. 51, 2167–2170 (1983)
Berry, M. V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 392, 45–57 (1984)
Berry, M. V. Classical adiabatic angles and quantal adiabatic phase. J. Phys. A 18, 15–27 (1985)
Hannay, J. H. Angle variable holonomy in adiabatic excursion of an integrable Hamiltonian. J. Phys. A 18, 221–230 (1985)
Arovas, D., Schrieffer, J. R. & Wilczek, F. Fractional statistics and the quantum Hall effect. Phys. Rev. Lett. 53, 722–723 (1984)
Tomita, A. & Chiao, R. Y. Observation of Berry’s topological phase by use of an optical fiber. Phys. Rev. Lett. 57, 937–940 (1986)
Kitaev, A. Y. Fault-tolerant quantum computation by anyons. Ann. Phys. 303, 2–30 (2003)
Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008)
Heiss, W. D. Phases of wave functions and level repulsion. Euro. Phys. J. D 7, 1–4 (1999)
Keck, F., Korsch, H. J. & Mossmann, S. Unfolding a diabolic point: a generalized crossing scenario. J. Phys. A 36, 2125–2137 (2003)
Berry, M. V. Physics of nonhermitian degeneracies. Czech. J. Phys. 54, 1039–1047 (2004)
Berry, M. V. & Uzdin, R. Slow non-Hermitian cycling: exact solutions and the Stokes phenomenon. J. Phys. A 44, 435303 (2011)
Uzdin, R., Mailybaev, A. & Moiseyev, N. On the observability and asymmetry of adiabatic state flips generated by exceptional points. J. Phys. A 44, 435302 (2011)
Milburn, T. J. et al. General description of quasiadiabatic dynamical phenomena near exceptional points. Phys. Rev. A 92, 052124 (2015)
Cartarius, H., Main, J. & Wunner, G. Exceptional points in the spectra of atoms in external fields. Phys. Rev. A 79, 053408 (2009)
Demange, G. & Graefe, E.-M. Signatures of three coalescing eigenfunctions. J. Phys. A 45, 025303 (2012)
Arnold, V. I. Mathematical Methods of Classical Mechanics Ch. 10 (Springer, 1989)
Ando, T., Nakanishi, T. & Saito, R. Berry’s phase and absence of back scattering in carbon nanotubes. J. Phys. Soc. Jpn 67, 2857–2862 (1998)
Lefebvre, R., Atabek, O., Šindelka, M. & Moiseyev, N. Resonance coalescence in molecular photodissociation. Phys. Rev. Lett. 103, 123003 (2009)
Hamamda, M., Pillet, P., Lignier, H. & Comparat, D. Ro-vibrational cooling of molecules and prospects. J. Phys. B 48, 182001 (2015)
Kaprálová-Žd’ánská, P. R. & Moiseyev, N. Helium in chirped laser fields as a time-asymmetric atomic switch. J. Chem. Phys. 141, 014307 (2014)
Kim, S. Braid operation of exceptional points. Fortschr. Phys. 61, 155–161 (2013)
Philipp, M., von Brentano, P., Pascovici, G. & Richter, A. Frequency and width crossing of two interacting resonances in a microwave cavity. Phys. Rev. E 62, 1922–1926 (2000)
Dembowski, C. et al. Experimental observation of the topological structure of exceptional points. Phys. Rev. Lett. 86, 787–790 (2001)
Thompson, J. D. et al. Strong dispersive coupling of a high-finesse cavity to a micromechanical membrane. Nature 452, 72–75 (2008)
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452 (2014)
Jing, H. et al. . -symmetric phonon laser. Phys. Rev. Lett. 113, 053604 (2014)
Graefe, E.-M., Mailybaev, A. A. & Moiseyev, N. Breakdown of adiabatic transfer of light in waveguides in the presence of absorption. Phys. Rev. A 88, 033842 (2013)
Jalas, D. et al. What is — and what is not — an optical isolator. Nat. Photon. 7, 579–582 (2013)
Underwood, M. et al. Measurement of the motional sidebands of a nanogram-scale oscillator in the quantum regime. Phys. Rev. A 92, 061801 (2015)
Shkarin, A. B. et al. Optically mediated hybridization between two mechanical modes. Phys. Rev. Lett. 112, 013602 (2014)
Choi, Y. et al. Quasieigenstate coalescence in an atom-cavity quantum composite. Phys. Rev. Lett. 104, 153601 (2010)
Lee, S.-B. et al. Observation of an exceptional point in a chaotic optical microcavity. Phys. Rev. Lett. 103, 134101 (2009)
Brandstetter, M. et al. Reversing the pump dependence of a laser at an exceptional point. Nat. Commun. 5, 4034 (2014)
Peng, B. et al. Loss-induced suppression and revival of lasing. Science 346, 328–332 (2014)
Zhen, B. et al. Spawning rings of exceptional points out of Dirac cones. Nature 525, 354–358 (2015)
Stehmann, T., Heiss, W. D. & Scholtz, F. G. Observation of exceptional points in electronic circuits. J. Phys. A 37, 7813–7819 (2004)
Gao, T. et al. Observation of non-Hermitian degeneracies in a chaotic exciton-polariton billiard. Nature 526, 554–558 (2015)
Heiss, W. D. & Nazmitdinov, R. G. Instabilities, nonhermiticity and exceptional points in the cranking model. J. Phys. A 40, 9475–9481 (2007)
Cartarius, H., Main, J. & Wunner, G. Discovery of exceptional points in the Bose-Einstein condensation of gases with attractive 1/r interaction. Phys. Rev. A 77, 013618 (2008)
Weidenmüller, H. A. Crossing of two Coulomb blockade resonances. Phys. Rev. B 68, 125326 (2003)
Wu, T.-T. & Huang, Z.-G. Level repulsions of bulk acoustic waves in composite materials. Phys. Rev. B 70, 214304 (2004)
Günther, U., Stefani, F. & Gerbeth, G. The MHD α2-dynamo, ℤ2-graded pseudo-Hermiticity, level crossings and exceptional points of branching type. Czech. J. Phys. 54, 1075–1089 (2004)
Michel, N., Nazarewicz, W., Okołowicz, J. & Płoszajczak, M. Open problems in the theory of nuclear open quantum systems. J. Phys. G 37, 064042 (2010)
Berry, M. V. Optical polarization evolution near a non-Hermitian degeneracy. J. Opt. 13, 115701 (2011)
Doppler, J. et al. Dynamically encircling an exceptional point for asymmetric mode switching. Nature http://www.dx.doi.org/10.1038/nature18605 (2016)
Acknowledgements
We thank L. Jiang, D. Lee, T. Milburn, P. Rabl, S. Rotter, A. Shkarin and W. Underwood for discussions. This work was supported by AFOSR Grant FA9550-15-1-0270.
Author information
Authors and Affiliations
Contributions
H.X., D.M. and L.J. performed the measurements and analysed the data. J.G.E.H. and H.X. wrote the manuscript with input from all the authors. J.G.E.H. directed the research.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
Extended Data Figure 1 Experimental schematics.
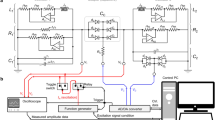
a, Illustration of the optical and electronic components. The measurement laser (‘ML’) is split into a local oscillator (‘LO’ in b) and a probe beam (‘Probe’ in b). The probe-beam frequency is shifted by an acousto-optic modulator (‘AOM1’), and is locked to the cavity using a Pound–Drever–Hall (PDH) scheme and modulation produced by an electro-optic modulator (‘EOM’). The control laser (‘CL’; ‘Control’ in b) is locked to the measurement laser with a frequency offset that is approximately double the free spectral range of the cavity. The control parameters used to access the EP are the power P and detuning Δ of the control laser. P and Δ are set by the amplitude and frequency of a signal generator (‘SG’), which drives another acousto-optic modulator (‘AOM3’). The PDH error signal is used to control the frequency of yet another acousto-optic modulator (‘AOM2’), ensuring that all beams track fluctuations of the cavity. Light is delivered to (and collected from) the cryostat via an optical circulator. Coloured lines, hollow lines and thick black lines show free-space laser beams, optical fibres and electrical circuits, respectively. Triangles, ovals and semicircles show electronics, fibre couplers and photodiodes, respectively. ‘DAQ’ indicates the data acquisition system. The silicon nitride membrane is shown in purple. b, Illustration of the optical frequency domain. Lasers are indicated by coloured arrows and cavity modes by black curves.
Extended Data Figure 2 Lock-in signal at low laser power (Δ = −780 kHz, P = 73 μW).
Left, amplitude (top, red) and phase angle (bottom, blue) of the lock-in signal as a function of drive frequency. Right, the same data shown as a parametric plot of the in-phase and out-of-phase components of the lock-in signal as a function of drive frequency.
Extended Data Figure 3 Lock-in signal at high laser power (Δ = −780 kHz, P = 380 μW).
Left, amplitude (top, red) and phase angle (bottom, blue) of the lock-in signal as a function of drive frequency. Right, the same data shown as a parametric plot of the in-phase and out-of-phase components of the lock-in signal as a function of drive frequency.
Rights and permissions
About this article
Cite this article
Xu, H., Mason, D., Jiang, L. et al. Topological energy transfer in an optomechanical system with exceptional points. Nature 537, 80–83 (2016). https://doi.org/10.1038/nature18604
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature18604
This article is cited by
-
Non-hermiticity in spintronics: oscillation death in coupled spintronic nano-oscillators through emerging exceptional points
Nature Communications (2024)
-
Robust temporal adiabatic passage with perfect frequency conversion between detuned acoustic cavities
Nature Communications (2024)
-
Chiral exceptional point and coherent suppression of backscattering in silicon microring with low loss Mie scatterer
eLight (2023)
-
Realization and topological properties of third-order exceptional lines embedded in exceptional surfaces
Nature Communications (2023)
-
Dynamically crossing diabolic points while encircling exceptional curves: A programmable symmetric-asymmetric multimode switch
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.