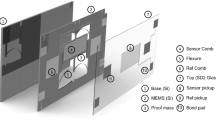
Abstract
The ability to measure tiny variations in the local gravitational acceleration allows, besides other applications, the detection of hidden hydrocarbon reserves, magma build-up before volcanic eruptions, and subterranean tunnels. Several technologies are available that achieve the sensitivities required for such applications (tens of microgal per hertz1/2): free-fall gravimeters1, spring-based gravimeters1,3, superconducting gravimeters4, and atom interferometers5. All of these devices can observe the Earth tides6: the elastic deformation of the Earth’s crust as a result of tidal forces. This is a universally predictable gravitational signal that requires both high sensitivity and high stability over timescales of several days to measure. All present gravimeters, however, have limitations of high cost (more than 100,000 US dollars) and high mass (more than 8 kilograms). Here we present a microelectromechanical system (MEMS) device with a sensitivity of 40 microgal per hertz1/2 only a few cubic centimetres in size. We use it to measure the Earth tides, revealing the long-term stability of our instrument compared to any other MEMS device. MEMS accelerometers—found in most smart phones7—can be mass-produced remarkably cheaply, but none are stable enough to be called a gravimeter. Our device has thus made the transition from accelerometer to gravimeter. The small size and low cost of this MEMS gravimeter suggests many applications in gravity mapping. For example, it could be mounted on a drone instead of low-flying aircraft for distributed land surveying and exploration, deployed to monitor volcanoes, or built into multi-pixel density-contrast imaging arrays.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Van Camp, M. Uncertainty of absolute gravity measurements. J. Geophys. Res. 110, B05406 (2005)
Jiang, Z. et al. Relative gravity measurement campaign during the 8th international comparison of absolute gravimeters (2009). Metrologia 49, 95–107 (2012)
Lederer, M. Accuracy of the relative gravity measurement. Acta Geodyn. Geomater. 6, 383–390 (2009)
Goodkind, J. M. The superconducting gravimeter. Rev. Sci. Instrum. 70, 4131–4152 (1999)
de Angelis, M. et al. Precision gravimetry with atomic sensors. Meas. Sci. Technol. 20, 022001 (2009)
Farrell, W. E. Earth tides, ocean tides and tidal loading. Phil. Trans. R. Soc. A 274, 253–259 (1973)
D’Alessandro, A. & D’Anna, G. Suitability of low-cost three-axis MEMS accelerometers in strong-motion seismology: tests on the LIS331DLH (iPhone) accelerometer. Bull. Seismol. Soc. Am. 103, 2906–2913 (2013)
Krishnamoorthy, U. et al. In-plane MEMS-based nano-g accelerometer with sub-wavelength optical resonant sensor. Sens. Actuat. A. 145–146, 283–290 (2008)
Lainé, J. & Mougenot, D. A high-sensitivity MEMS-based accelerometer. Leading Edge 33, 1234–1242 (2014)
Pike, W. T. et al. A self-levelling nano-g silicon seismometer. In Proc. IEEE Sensors 2014 1599–1602, http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=6985324 (IEEE, 2014)
Bertolini, A., Cella, G., Desalvo, R. & Sannibale, V. Seismic noise filters, vertical resonance frequency reduction with geometric anti-springs: a feasibility study. Nucl. Instrum. Meth. A 435, 475–483 (1999)
Cella, G. et al. Seismic attenuation performance of the first prototype of a geometric antispring filter. Nucl. Instrum. Meth. A 487, 652–660 (2002)
Pike, W. T., Standley, I. M. & Calcutt, S. A silicon microseismometer for Mars. In Transducers and Eurosensors XXVII 622–625, http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=6626843 (IEEE, 2013)
Carbone, L. et al. Sensors and actuators for the Advanced LIGO mirror suspensions. Class. Quantum Gravity 29, 115005 (2012)
Bell, C. J., Reid, S. & Faller, J. Experimental results for nulling the effective thermal expansion coefficient of fused silica fibres under a static stress. Class. Quantum Gravity 31, 065010 (2014)
Watanabe, H., Yamada, N. & Okaji, M. Linear thermal expansion coefficient of silicon from 293 to 1000 K. Int. J. Thermophys. 25, 221–236 (2004)
Poggi, M. A., McFarland, A. W., Colton, J. S. & Bottomley, L. A. A method for calculating the spring constant of atomic force microscopy cantilevers with a nonrectangular cross section. Anal. Chem. 77, 1192–1195 (2005)
Cho, C. H. Characterization of Young’s modulus of silicon versus temperature using a “beam deflection” method with a four-point bending fixture. Curr. Appl. Phys. 9, 538–545 (2009)
Van Camp, M. & Vauterin, P. Tsoft: graphical and interactive software for the analysis of time series and Earth tides. Comput. Geosci. 31, 631–640 (2005)
Callen, H. B. & Welton, T. A. Irreversibility and generalized noise. Phys. Rev. 83, 34–40 (1951)
Chin, E., Lee, K., Winterood, J., Ju, L. & Blair, D. Low frequency vertical geometric anti-spring vibration isolators. Phys. Lett. A 336, 97–105 (2005)
Sainz-Maza Aparicio, S., Sampedro, J. A., Montesinos, F. G. & Molist, J. M. Volcanic signatures in time gravity variations during the volcanic unrest on El Hierro (Canary Islands). J. Geophys. Res. 119, 5033–5051 (2014)
Mogi, K. Relations between the eruptions of various volcanoes and the deformations of the ground surfaces around them. Bull. Earthq. Res. Inst. 36, 99–134 (1958)
Battaglia, M., Gottsmann, J., Carbone, D. & Fernandez, J. 4D volcano gravimetry. Geophysics 73, WA3–WA18 (2008)
Rymer, H., Williams-Jones, G. & Keynes, M. Gravity and deformation measurements. Geophys. Res. Lett. 27, 2389–2392 (2000)
Allan, D. Statistics of atomic frequency standards. Proc. IEEE 54, 221–230 (1966)
Peterson, J. Observations and modeling of seismic background noise. US Geological Survey Open-file Report Number 93-322, http://www.mttmllr.com/ADS/DATA/peterson_usgs_seismic_noise_ofr93-322.pdf (USGS, 1993)
Essen, H. H., Kruger, F., Dahm, T. & Grevemeyer, I. On the generation of secondary micro-seisms observed in northern and central Europe. J. Geophys. Res. 108, 2506–2520 (2003)
Baxter, P. J. & Gresham, A. Deaths and injuries in the eruption of Galeras volcano, Colombia, 14 January 1993. J. Volcanol. Geotherm. Res. 77, 325–338 (1997)
Riccardi, U., Rosat, S. & Hinderer, J. Comparison of the Micro-g LaCoste gPhone-054 spring gravimeter and the GWR-C026 superconducting gravimeter in Strasbourg (France) using a 300-day time series. Metrologia 48, 28–39 (2011)
Pike, W. Analysis of sidewall quality in through-wafer deep reactive-ion etching. Microelectron. Eng. 73–74, 340–345 (2004)
Laermer, F. & Schilp, A. Method of anisotropic etching of silicon. US patent number 5,501,893 (1996)
Rim, H. & Li, Y. Advantages of borehole vector gravity in density imaging. Geophysics 80, G1–G13 (2015)
Bauer-gottwein, P., Christiansen, L. & Rosbjerg, D. Informing hydrological models with ground-based time-lapse relative gravimetry: potential and limitations. In Proc. Symp. J-H01 (GRACE, Remote Sensing and Ground-based Methods in Multi-Scale Hydrology) 187–194 (IAHS Publ. 343, 2011)
Romaides, A. J. et al. A comparison of gravimetric techniques for measuring subsurface void signals. J. Phys. D 34, 433–443 (2001)
Butler, D. K. Microgravimetric and gravity gradient techniques for detection of subsurface cavities. Geophysics 49, 1084–1096 (1984)
Kirkendall, B., Li, Y. & Oldenburg, D. Imaging cargo containers using gravity gradiometry. IEEE Trans. Geosci. Remote Sens. 45, 1786–1797 (2007)
Acknowledgements
The work was funded by the Royal Society Paul Instrument Fund and STFC grant number ST/M000427/1. We thank M. Pitkin for advice on completing statistical significance tests on the data, W. Cunningham for advice on finite element modelling, M. Perreur-Lloyd and R. Jones for their help in rendering three-dimensional images of the apparatus, and the staff and other users of the James Watt Nanofabrication Centre for help and support in undertaking the MEMS fabrication.
Author information
Authors and Affiliations
Contributions
R.P.M. led the methodology of the etch process for the MEMS gravimeter and worked with G.D.H. on the development of the MEMS gravimeter. G.D.H. and R.P.M. enhanced the long-term, low-noise stability of the entire system, taking the tide data and performing the computational analysis. R.P.M. led writing the manuscript. A.S. led the methodology of the MEMS mask fabrication. A.S. and R.P.M. took the tide measurements in early 2015 and performed computational analysis of the MEMS gravimeter. D.J.P. supervised the design of the MEMS device fabrication process and with G.D.H. came up with the concept for a MEMS gravity sensor. J.H. developed the methodology of utilizing geometric anti-springs for the MEMS gravimeter system and commented on the manuscript. S.R. was responsible for the resources that were necessary to complete the project and commented on the manuscript. G.D.H. had the initial concept of a MEMS gravimeter together with D.J.P. G.D.H. had oversight of the design, fabrication and testing of the gravimeter (via the supervision of R.P.M. and A.S.). R.P.M. and G.D.H. characterized and enhanced the low noise performance, resulting in the measurement of the tides. G.D.H. was responsible for acquiring the funding for the work.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
The research data relevant to this Letter are stored on the University of Glasgow’s Enlighten Repository (http://dx.doi.org/10.5525/gla.researchdata.213).
Extended data figures and tables
Extended Data Figure 1 Spring resonant frequency behaviour with tilt.
The resonant frequency decreases as the MEMS device gets closer to vertical due to the geometrical anti-spring effect. At 88° and 92° there are minima in the plot (see inset). At this point the frequency is constant with tilt and the system displays Hooke’s law behaviour. The resonant frequency of a symmetric anti-spring would reach an instability here. This figure also demonstrates that while the instrument is operated at 90° the resonant frequency is 2.3 Hz. It can be lowered to 1.8–1.9 Hz by tilting to operate at one of the minima.
Extended Data Figure 2 The Earth tides with different filtering.
a, Measurements of the Earth tides obtained from the MEMS device. This is the raw data output. b, The same data but with a 10-min filtering time. The red lines are theoretical plots calculated by TSOFT. The blue lines are the experimental data.
Extended Data Figure 3 Quality factor frequency dependence.
We observe a trend of decreasing quality factor with decreasing frequency of our device. At low frequencies the internal friction of the material becomes the dominant loss mechanism. This trend has been discussed by ref. 21.
Extended Data Figure 4 Geometrical anti-spring design.
a and b demonstrate the Hooke’s law behaviour of a straight and curved cantilever, respectively. c and d demonstrate the unstable anti-spring characteristics of a 2- and 4-flexure MEMS device, respectively. e, The behaviour of a 3-flexure MEMS device (see Fig. 1). Whereas a 2- or 4-flexure system reaches an instability with increasing load, a 3-flexure system regains Hooke’s law behaviour. The 3-flexure system behaves as such because it is pushed off its constrained axis by the asymmetry of the design. All of these plots were produced using Ansys finite element analysis software (http://www.ansys.com/en-GB).
Extended Data Figure 5 Polynomial drift.
This plot demonstrates the drift in the data shortly after the vacuum pump has been turned on. A polynomial component to the drift is clearly visible. Once the vacuum system has settled, however, the drift becomes linear, as demonstrated in Fig. 4b, at a level of 150 μGal per day.
Extended Data Figure 6 MEMS device root-mean-square acceleration sensitivity.
a, The root-mean-square acceleration sensitivity in microgal. b, The root-mean-square acceleration sensitivity in decibel microgal. The tide signal can be observed in both plots at 10−5 Hz; the peak at 2 × 10−3 Hz is the artefact of the temperature servo discussed earlier; the microseismic peak can be observed between 0.1 Hz and 0.2 Hz; and the 2.3-Hz resonant frequency can be observed to the right of the plot (the blue spike at just above 1 Hz). Two different sampling rates were used to capture this data. The blue series was captured at a sampling rate of 70 Hz while the red series was captured at a sampling rate of 0.05 Hz. This was done to minimize the size of the data file.
Extended Data Figure 7 Power spectral density comparison.
The red line—plotted using the data from Fig. 4g—represents our MEMS device, demonstrating its sensitivity in the tidal frequency range. The filtering time means that the sensitivity rolls off above 10−4 Hz. The black line represents the Scintrex CG5, the blue line the Micro-g Lacoste gPhone-054, the green line the SG-C026 superconducting gravimeter. The data from these three series are taken from figure 8 in ref. 30 (copyright Bureau International des Poids et Mesures, reproduced by permission of IOP Publishing, all rights reserved). The magenta series represents the microseismometer by W. T. Pike et al. (private communication by permission of the author, to be published in the 47th Lunar and Planetary Science Conference).
Extended Data Figure 8 Tilt susceptibility tests.
a, The variation in output of the MEMS device with the x-axis tilt of the sensor plotted on a secondary axis. b, The same as a but for the y axis. There is an y-axis (in-plane MEMS tilt) tilt sensitivity in this axis of 21.2 μGal per arcsecond, but in the x axis (out-of-plane MEMS tilt) the tilt sensitivity is only 0.6 μGal per arcsecond.
Extended Data Figure 9 Long-term reproducibility tests.
a and b are two data sets separated by approximately 4 months, with no filtering employed. During this period the vacuum chamber was evacuated and vented several times, but despite this the calibration factor of the device has not changed by more than 5%.
Rights and permissions
About this article
Cite this article
Middlemiss, R., Samarelli, A., Paul, D. et al. Measurement of the Earth tides with a MEMS gravimeter. Nature 531, 614–617 (2016). https://doi.org/10.1038/nature17397
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature17397
This article is cited by
-
A self-centering and stiffness-controlled MEMS accelerometer
Microsystems & Nanoengineering (2024)
-
Measuring picometre-level displacements using speckle patterns produced by an integrating sphere
Scientific Reports (2023)
-
Higher-order singularities in phase-tracked electromechanical oscillators
Nature Communications (2023)
-
Simultaneous cavity cooling of all six degrees of freedom of a levitated nanoparticle
Nature Physics (2023)
-
Electrostatic nonlinear dispersive parametric mode interaction
Nonlinear Dynamics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.