Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

The Parkfield tremors reveal slow and fast ruptures on the same asperity

Nature volume 532, pages 361–365 (2016)Cite this article

Subjects

Abstract

The deep extension of the San Andreas Fault is believed to be creeping, but the recent observations of tectonic tremors from these depths indicate a complex deformation style1. In particular, an isolated tremor source near Parkfield has been producing a sequence of low-frequency earthquakes2 that indicates an uncommon mechanism of stress accumulation and release. The tremor pattern regularly oscillated between three and six days from mid-2003 until it was disrupted by the 2004 magnitude 6.0 Parkfield earthquake. After that event, the tremor source ruptured only about every three days, but over the next two years it gradually returned to its initial alternating recurrence pattern. The mechanism that drives this recurrence pattern is unknown. Here we use physics-based models to show that the same tremor asperity—the region from which the low-frequency earthquakes radiate—can regularly slip in slow and fast ruptures, naturally resulting in recurrence intervals alternating between three and six days. This unusual slip behaviour occurs when the tremor asperity size is close to the critical nucleation size of earthquakes. We also show that changes in pore pressure following the Parkfield earthquake can explain the sudden change and gradual recovery of the recurrence intervals. Our findings suggest a framework for fault deformation in which the same asperity can release tectonic stress through both slow and fast ruptures.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Figure 1: The Parkfield tremors.
Figure 2: Recurrence pattern and source characteristics of the period-doubling Parkfield tremors and numerical simulations.
Figure 3: The modelled mechanics behind the period-doubling tremors.

References

  1. Shelly, D. R. Migrating tremors illuminate complex deformation beneath the seismogenic San Andreas Fault. Nature 463, 648–652 (2010)

    ADS  PubMed  CAS  Google Scholar 

  2. Shelly, D. R. Periodic, chaotic, and doubled earthquake recurrence intervals on the deep San Andreas Fault. Science 328, 1385–1388 (2010)

    ADS  PubMed  CAS  Google Scholar 

  3. Shelly, D. R. Complexity of the deep San Andreas Fault zone defined by cascading tremor. Nature Geosci. 8, 145–151 (2015)

    ADS  CAS  Google Scholar 

  4. Ito, Y., Obara, K., Shiomi, K., Sekine, S. & Hirose, H. Slow earthquakes coincident with episodic tremors and slow slip events. Science 315, 503–506 (2007)

    ADS  PubMed  CAS  Google Scholar 

  5. Schwartz, S. Y. & Rokosky, J. M. Slow slip events and seismic tremor at circum-Pacific subduction zones. Rev. Geophys. 45, RG3004 (2007)

    ADS  Google Scholar 

  6. Daub, E. G., Shelly, D. R., Guyer, R. A. & Johnson, P. A. Brittle and ductile friction and the physics of tectonic tremor. Geophys. Res. Lett. 38, L10301 (2011)

    ADS  Google Scholar 

  7. Ghosh, A., Vidale, J. E. & Creager, K. C. Tremor asperities in the transition zone control evolution of slow earthquakes. J. Geophys. Res. 117, B10301 (2012)

    ADS  Google Scholar 

  8. Gu, Y. & Wong, T.-F. in Nonlinear Dynamics and Predictability of Geophysical Phenomena (eds Newman, W. I., Gabrielov, A. & Turcotte, D. L. ) 15–35 (Geophys. Monogr. 83, AGU, 1994)

    Google Scholar 

  9. Dieterich, J. H. Modeling of rock friction 1. Experimental results and constitutive equations. J. Geophys. Res. 84, 2161–2168 (1979)

    ADS  Google Scholar 

  10. Scholz, C. H. Earthquakes and friction laws. Nature 391, 37–42 (1998)

    ADS  CAS  Google Scholar 

  11. Lapusta, N. & Barbot, S. in The Mechanics of Faulting: From Laboratory to Real Earthquakes (eds Bizzarri, A. & Bhat, H. S. ) 153–207 (Research Signpost, 2012)

  12. Noda, H. & Lapusta, N. Three-dimensional earthquake sequence simulations with evolving temperature and pore pressure due to shear heating: effect of heterogeneous hydraulic diffusivity. J. Geophys. Res. 115, B12314 (2010)

    ADS  Google Scholar 

  13. Barbot, S., Lapusta, N. & Avouac, J.-P. Under the hood of the earthquake machine: towards predictive modeling of the seismic cycle. Science 336, 707–710 (2012)

    ADS  PubMed  CAS  Google Scholar 

  14. Rubin, A. M. & Ampuero, J.-P. Earthquake nucleation on (aging) rate and state faults. J. Geophys. Res. 110, B11312 (2005)

    ADS  Google Scholar 

  15. Liu, Y. & Rice, J. R. Spontaneous and triggered aseismic deformation transients in a subduction fault model. J. Geophys. Res. 112, B09404 (2007)

    ADS  Google Scholar 

  16. Matsuzawa, T., Hirose, H., Shibazaki, B. & Obara, K. Modeling short- and long-term slow slip events in the seismic cycles of large subduction earthquakes. J. Geophys. Res. 115, B12301 (2010)

    ADS  Google Scholar 

  17. Noda, H. & Hori, T. Under what circumstances does a seismogenic patch produce aseismic transients in the later interseismic period? Geophys. Res. Lett. 41, 7477–7484 (2014)

    ADS  Google Scholar 

  18. Rubinstein, J. L. et al. Non-volcanic tremor driven by large transient shear stresses. Nature 448, 579–582 (2007)

    ADS  PubMed  CAS  Google Scholar 

  19. Peng, Z. et al. Strong tremor near Parkfield, CA, excited by the 2002 Denali Fault earthquake. Geophys. Res. Lett. 35, L23305 (2008)

    ADS  Google Scholar 

  20. Thomas, A. M., Nadeau, R. M. & Bürgmann, R. Tremor-tide correlations and near-lithostatic pore pressure on the deep San Andreas Fault. Nature 462, 1048–1051 (2009)

    ADS  PubMed  CAS  Google Scholar 

  21. Ide, S. Striations, duration, migration and tidal response in deep tremor. Nature 466, 356–359 (2010)

    ADS  PubMed  CAS  Google Scholar 

  22. Brenguier, F. et al. Postseismic relaxation along the San Andreas Fault at Parkfield from continuous seismological observations. Science 321, 1478–1481 (2008)

    ADS  PubMed  CAS  Google Scholar 

  23. Segall, P., Rubin, A. M., Bradley, A. M. & Rice, J. R. Dilatant strengthening as a mechanism for slow slip events. J. Geophys. Res. 115, B12305 (2010)

    ADS  Google Scholar 

  24. Rubin, A. M. Designer friction laws for bimodal slow slip propagation speeds. Geochem. Geophys. Geosyst. 12, Q04007 (2011)

    ADS  Google Scholar 

  25. Ito, Y. et al. Episodic slow slip events in the Japan subduction zone before the 2011 Tohoku-Oki earthquake. Tectonophysics 600, 14–26 (2013)

    ADS  Google Scholar 

  26. Meng, L., Huang, H., Bürgmann, R., Ampuero, J.-P. & Strader, A. Dual megathrust slip behaviors of the 2014 Iquique earthquake sequence. Earth Planet. Sci. Lett. 411, 177–187 (2015)

    ADS  CAS  Google Scholar 

  27. Shelly, D. R. & Hardebeck, J. L. Precise tremor source locations and amplitude variations along the lower-crustal central San Andreas Fault. Geophys. Res. Lett. 37, L14301 (2010)

    ADS  Google Scholar 

  28. Tape, C., Plesch, A., Shaw, J. H. & Gilbert, H. Estimating a continuous Moho surface from the California Unified Velocity Model. Seismol. Res. Lett. 83, 728–735 (2012)

    Google Scholar 

  29. Lapusta, N. & Liu, Y. Three-dimensional boundary integral modeling of spontaneous earthquake sequences and aseismic slip. J. Geophys. Res. 114, B09303 (2009)

    ADS  Google Scholar 

  30. Harris, R. A. et al. The SCEC/USGS dynamic earthquake rupture code verification exercise. Seismol. Res. Lett. 80, 119–126 (2009)

    Google Scholar 

  31. Chen, T. & Lapusta, N. Scaling of small repeating earthquakes explained by interaction of seismic and aseismic slip in a rate and state fault model. J. Geophys. Res. 114, B01311 (2009)

    ADS  Google Scholar 

  32. Kaneko, Y., Avouac, J.-P. & Lapusta, N. Towards inferring earthquake patterns from geodetic observations of interseismic coupling. Nature Geosci. 3, 363–369 (2010)

    ADS  CAS  Google Scholar 

  33. Marone, C. Laboratory-derived friction laws and their application to seismic faulting. Annu. Rev. Earth Planet. Sci. 26, 643–696 (1998)

    ADS  CAS  Google Scholar 

  34. Ruina, A. Slip instability and state variable friction laws. J. Geophys. Res. 88, 10359–10370 (1983)

    ADS  Google Scholar 

  35. Rice, J. R. & Ruina, A. L. Stability of steady frictional slipping. J. Appl. Mech. 50, 343–349 (1983)

    ADS  MATH  Google Scholar 

  36. Dieterich, J. H. in Treatise on Geophysics Vol. 4, Earthquake Seismology (ed. Kanamori, H. ) 107–129 (Elsevier Science, 2007)

  37. Rice, J. R. & Ben-Zion, Y. Slip complexity in earthquake fault models. Proc. Natl. Acad. Sci. 93, 3811–3818 (1996)

    ADS  PubMed  CAS  Google Scholar 

  38. Marone, C. & Kilgore, B. Scaling of the critical slip distance for seismic faulting with shear strain in fault zones. Nature 362, 618–621 (1993)

    ADS  Google Scholar 

  39. Rice, J. R., Lapusta, N. & Ranjith, K. Rate and state dependent friction and the stability of sliding between elastically deformable solids. J. Mech. Phys. Solids 49, 1865–1898 (2001)

    ADS  MATH  Google Scholar 

  40. Beeler, N. M., Thomas, A., Bürgmann, R. & Shelly, D. R. Inferring fault rheology from low-frequency earthquakes on the San Andreas. J. Geophys. Res. 118, 5976–5990 (2013)

    ADS  Google Scholar 

  41. Peng, Z., Vidale, J. E., Wech, A. G., Nadeau, R. M. & Creager, K. C. Remote triggering of tremor along the San Andreas Fault in central California. J. Geophys. Res. 114, B00A06 (2009)

    ADS  Google Scholar 

  42. Shelly, D. R., Peng, Z., Hill, D. P. & Aiken, C. Triggered creep as a possible mechanism for delayed dynamic triggering of tremor and earthquakes. Nature Geosci. 4, 384–388 (2011)

    ADS  CAS  Google Scholar 

  43. Thomas, A. M., Bürgmann, R., Shelly, D. R., Beeler, N. M. & Rudolph, M. L. Tidal triggering of low frequency earthquakes near Parkfield, CA: implications for fault mechanics within the brittle-ductile transition. J. Geophys. Res. 117, B05301 (2012)

    ADS  Google Scholar 

  44. Zigone, D. et al. Triggering of tremors and slow slip event in Guerrero, Mexico, by the 2010 Mw 8.8 Maule, Chile, earthquake. J. Geophys. Res. 117, B09304 (2012)

    ADS  Google Scholar 

  45. Noda, H. & Lapusta, N. Stable creeping fault segments can become destructive as a result of dynamic weakening. Nature 493, 518–521 (2013)

    ADS  PubMed  CAS  Google Scholar 

  46. Barbot, S. & Fialko, Y. A unified continuum representation of post-seismic relaxation mechanisms: semi-analytic models of afterslip, poroelastic rebound and viscoelastic flow. Geophys. J. Int. 182, 1124–1140 (2010)

    ADS  Google Scholar 

Download references

Acknowledgements

We thank D. R. Shelly for sharing his tremor data and J.-P. Avouac for his comments on an earlier version of the manuscript. This work comprises Earth Observatory of Singapore contribution no. 115. S.B. is funded by the National Research Foundation Singapore under its Singapore NRF Fellowship scheme (National Research Fellow Award no. NRF-NRFF2013-04), by the Earth Observatory of Singapore, by the National Research Foundation Singapore and by the Singapore Ministry of Education under the Research Centres of Excellence initiative.

Author information

Authors and Affiliations

  1. Earth Observatory of Singapore, Asian School of the Environment, Nanyang Technological University, 50 Nanyang Avenue, Singapore, 639798, Singapore

    Deepa Mele Veedu & Sylvain Barbot

Authors
  1. Deepa Mele Veedu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sylvain Barbot
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

D.M.V. and S.B. designed the experiment, analysed the data, and wrote the paper.

Corresponding authors

Correspondence to Deepa Mele Veedu or Sylvain Barbot.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Extended data figures and tables

Extended Data Figure 1 Numerical model of the Parkfield tremors.

a, Schematic diagram of the model geometry and frictional properties. A square velocity-weakening patch (yellow) is embedded in a large velocity-strengthening fault domain. R is the asperity size of the patch. The entire fault domain is driven by a plate rate of Vpl = 3 cm yr−1. h* (dotted circle) is the critical nucleation size of the velocity-weakening patch to generate elasto-dynamic slip. We use the ratio R/h* = 0.73. The model has R = 3 m, L = 5 μm and an effective confining pressure of  = 50 MPa, but period-doubling recurrence intervals at three and six days can be obtained for various asperity sizes, as discussed in the text. b, The yellow square patch in a produces a succession of slow and fast ruptures. Fast ruptures may be detected in seismograms and may coincide with one of the LFEs. The model reproduces the period-doubling recurrence pattern of the Parkfield tremors before the 2004 Parkfield earthquake.

Extended Data Figure 2 Recurrence pattern and source characteristics of the period-doubling Parkfield tremors and numerical simulations with slip velocity.

a–d, Same as Fig. 2, but plotting slip velocity (instead of slip) in c and d.

Extended Data Figure 3 Simulations of period-doubling sequences of slow and fast ruptures along eight orders of magnitude.

All simulations assume the same rheological parameters except for the characteristic weakening distance L, which is used to adjust the ratio R/h* to within the period-doubling range. a, With R = 3 m and L = 5μm, we obtained slow and fast ruptures with an equivalent geodetic moment magnitude of Mw −1.9 and Mw −0.5. b, With R = 30 m and L = 0.05 mm, the range is Mw 0.07 and Mw 1.4. c, For R = 300 m and L = 0.5 mm, the range is Mw 2.1 and Mw 3.5. d, For R = 3 km and L = 5 mm, the range is Mw 3.9 and Mw 5.4. Square patches of velocity-weakening friction with different sizes may exhibit period doubling at almost all magnitudes. The blue and red lines show aseismic and seismic slip, respectively. VS and VW represent the extent of the velocity strengthening and velocity weakening regions, respectively. Increments refer to the time steps between consecutive profiles (larger for aseismic than for seismic slip).

Extended Data Figure 4 Potential of non-circular shaped asperities to produce complex sequences of slow and fast ruptures with period doubling.

a, c, Velocity-weakening (VW) patches with two different shapes. b, d, The corresponding history of the period separating each event (a and c respectively). For both simulations, we assume the same frictional parameters and confining pressure. Elliptical (and potentially other non-circular) patches can produce period doubling over a wider range of parameters than a circular asperity can. With the parameters considered, the non-circular asperities produce period doubling of recurrence time, but the circular patch does not. The parameters considered are 50 MPa, a = 10−2, L = 5 μm, and the velocity-weakening regions are characterized by (a − b) = −4 × 10−3, while the velocity-strengthening regions have (a − b) = +4 × 10−3. Slip events (seismic and aseismic) are singled out when the slip velocity threshold reaches the value Vth = 10−4 m s−1.

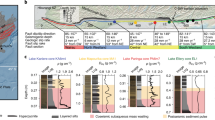
Extended Data Figure 5 Simulation of the recurrence intervals of the period-doubling Parkfield tremors in a larger slip patch with R = 33 m and  = 5 MPa.

a, Numerical simulation of the Parkfield tremor activity incorporating the change in effective pore pressure (red profile) after the Parkfield earthquake (EQ; vertical dashed line). The coloured dots denote the maximum velocity of the slip events. The slip events are flagged when the slip velocity is above the threshold Vpl = 10−4 m s−1 anywhere along the fault. Fast ruptures are preceded by shorter recurrence intervals. A change of pore pressure of about 300 kPa, representing 6% of the effective confining pressure, is applied at the onset of the Parkfield earthquake, resulting in a rapid occurrence of slip events, followed by a sequence of multiplets (highlighted in the two boxes) with varying period-multiplying factors. The pressure perturbation is chosen by trial and error to create a two-year transient that is similar to the seismic observations. The top right inset shows the model geometry with an asperity size R of 33 m. b, Characterization of the dynamics of the slip events. Fast ruptures are preceded by shorter recurrence intervals. The effective pore-pressure perturbation following the Parkfield earthquake affects the dynamics of the sequence with a temporary interruption of period doubling followed by a gradual recovery. See Fig. 2 legend for details of methodology and presentation.

PowerPoint slides

Rights and permissions

Reprints and Permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Veedu, D., Barbot, S. The Parkfield tremors reveal slow and fast ruptures on the same asperity. Nature 532, 361–365 (2016). https://doi.org/10.1038/nature17190

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nature17190

This article is cited by

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing