Abstract
The quantum nature of the proton can crucially affect the structural and physical properties of hydrogen compounds. For example, in the high-pressure phases1,2 of H2O, quantum proton fluctuations lead to symmetrization of the hydrogen bond and reduce the boundary between asymmetric and symmetric structures in the phase diagram by 30 gigapascals (ref. 3). Here we show that an analogous quantum symmetrization occurs in the recently discovered4 sulfur hydride superconductor with a superconducting transition temperature Tc of 203 kelvin at 155 gigapascals—the highest Tc reported for any superconductor so far. Superconductivity occurs via the formation of a compound with chemical formula H3S (sulfur trihydride) with sulfur atoms arranged on a body-centred cubic lattice5,6,7,8,9. If the hydrogen atoms are treated as classical particles, then for pressures greater than about 175 gigapascals they are predicted to sit exactly halfway between two sulfur atoms in a structure with  symmetry. At lower pressures, the hydrogen atoms move to an off-centre position, forming a short H–S covalent bond and a longer H···S hydrogen bond in a structure with R3m symmetry5,6,7,8,9. X-ray diffraction experiments confirm the H3S stoichiometry and the sulfur lattice sites, but were unable to discriminate between the two phases10. Ab initio density-functional-theory calculations show that quantum nuclear motion lowers the symmetrization pressure by 72 gigapascals for H3S and by 60 gigapascals for D3S. Consequently, we predict that the
symmetry. At lower pressures, the hydrogen atoms move to an off-centre position, forming a short H–S covalent bond and a longer H···S hydrogen bond in a structure with R3m symmetry5,6,7,8,9. X-ray diffraction experiments confirm the H3S stoichiometry and the sulfur lattice sites, but were unable to discriminate between the two phases10. Ab initio density-functional-theory calculations show that quantum nuclear motion lowers the symmetrization pressure by 72 gigapascals for H3S and by 60 gigapascals for D3S. Consequently, we predict that the  phase dominates the pressure range within which the high Tc was measured. The observed pressure dependence of Tc is accurately reproduced in our calculations for the
phase dominates the pressure range within which the high Tc was measured. The observed pressure dependence of Tc is accurately reproduced in our calculations for the  phase, but not for the R3m phase. Therefore, the quantum nature of the proton fundamentally changes the superconducting phase diagram of H3S.
phase, but not for the R3m phase. Therefore, the quantum nature of the proton fundamentally changes the superconducting phase diagram of H3S.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Goncharov, A. F., Struzhkin, V. V., Somayazulu, M. S., Hemley, R. J. & Mao, H. K. Compression of ice to 210 gigapascals: infrared evidence for a symmetric hydrogen-bonded phase. Science 273, 218–220 (1996)
Loubeyre, P., LeToullec, R., Wolanin, E., Hanfland, M. & Hausermann, D. Modulated phases and proton centring in ice observed by X-ray diffraction up to 170 GPa. Nature 397, 503–506 (1999)
Benoit, M., Marx, D. & Parrinello, M. Tunnelling and zero-point motion in high-pressure ice. Nature 392, 258–261 (1998)
Drozdov, A. P., Eremets, M. I., Troyan, I. A., Ksenofontov, V. & Shylin, S. I. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 525, 73–76 (2015)
Duan, D. et al. Pressure-induced metallization of dense (H2S)2H2 with high-Tc superconductivity. Sci. Rep. 4, 6968 (2014)
Duan, D. et al.. Pressure-induced decomposition of solid hydrogen sulfide. Phys. Rev. B 91, 180502 (2015)
Errea, I. et al. High-pressure hydrogen sulfide from first principles: a strongly anharmonic phonon-mediated superconductor. Phys. Rev. Lett. 114, 157004 (2015)
Li, Y. et al. Dissociation products and structures of solid H2S at strong compression. Phys. Rev. B 93, 020103(R) (2016)
Bernstein, N., Hellberg, C. S., Johannes, M. D., Mazin, I. I. & Mehl, M. J. What superconducts in sulfur hydrides under pressure and why. Phys. Rev. B 91, 060511 (2015)
Einaga, M. et al. Crystal structure of 200 K-superconducting phase of sulfur hydride system. Preprint at http://arXiv.org/abs/1509.03156 (2015)
Landau, L. D. & Lifshitz, E. M. Statistical Physics 3rd edn, Vol. 5 of Course of Theoretical Physics (Butterworth-Heinemann, 1980)
Papaconstantopoulos, D. A., Klein, B. M., Mehl, M. J. & Pickett, W. E. Cubic H3S around 200 GPa: an atomic hydrogen superconductor stabilized by sulfur. Phys. Rev. B 91, 184511 (2015)
Akashi, R., Kawamura, M., Tsuneyuki, S., Nomura, Y. & Arita, R. First-principles study of the pressure and crystal-structure dependences of the superconducting transition temperature in compressed sulfur hydrides. Phys. Rev. B 91, 224513 (2015)
Nicol, E. J. & Carbotte, J. P. Comparison of pressurized sulfur hydride with conventional superconductors. Phys. Rev. B 91, 220507 (2015)
Flores-Livas, J. A., Sanna, A. & Gross, E. K. U. High temperature superconductivity in sulfur and selenium hydrides at high pressure. Preprint at http://arXiv.org/abs/1501.06336 (2015)
Li, Y., Hao, J., Liu, H., Li, Y. & Ma, Y. The metallization and superconductivity of dense hydrogen sulfide. J. Chem. Phys. 140, 174712 (2014)
Bianconi, A. & Jarlborg, T. Superconductivity above the lowest earth temperature in pressurized sulfur hydride. Europhys. Lett. 112, 37001 (2015)
Hirsch, J. E. & Marsiglio, F. Hole superconductivity in H2S and other sulfides under high pressure. Physica C 511, 45–49 (2015)
Lee, C., Vanderbilt, D., Laasonen, K., Car, R. & Parrinello, M. Ab initio studies on high pressure phases of ice. Phys. Rev. Lett. 69, 462–465 (1992)
Lee, C., Vanderbilt, D., Laasonen, K., Car, R. & Parrinello, M. Ab initio studies on the structural and dynamical properties of ice. Phys. Rev. B 47, 4863–4872 (1993)
McMahon, M. I. et al. Geometric effects of deuteration on hydrogen-ordering phase transitions. Nature 348, 317–319 (1990)
Errea, I., Calandra, M. & Mauri, F. First-principles theory of anharmonicity and the inverse isotope effect in superconducting palladium-hydride compounds. Phys. Rev. Lett. 111, 177002 (2013)
Errea, I., Calandra, M. & Mauri, F. Anharmonic free energies and phonon dispersions from the stochastic self-consistent harmonic approximation: application to platinum and palladium hydrides. Phys. Rev. B 89, 064302 (2014)
Song, M., Yamawaki, H., Fujihisa, H., Sakashita, M. & Aoki, K. Infrared investigation on ice VIII and the phase diagram of dense ices. Phys. Rev. B 68, 014106 (2003)
Goncharov, A. F., Struzhkin, V. V., Mao, H. K. & Hemley, R. J. Raman spectroscopy of dense H2O and the transition to symmetric hydrogen bonds. Phys. Rev. Lett. 83, 1998–2001 (1999)
Caracas, R. Dynamical instabilities of ice X. Phys. Rev. Lett. 101, 085502 (2008)
Marqués, M., Ackland, G. J. & Loveday, J. S. Nature and stability of ice X. High Press. Res. 29, 208–211 (2009)
Bronstein, Y., Depondt, P., Finocchi, F. & Saitta, A. M. Quantum-driven phase transition in ice described via an efficient Langevin approach. Phys. Rev. B 89, 214101 (2014)
Calandra, M., Profeta, G. & Mauri, F. Adiabatic and nonadiabatic phonon dispersion in a Wannier function approach. Phys. Rev. B 82, 165111 (2010)
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996)
Baroni, S., de Gironcoli, S., Dal Corso, A. & Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 73, 515–562 (2001)
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009)
Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 41, 7892–7895 (1990)
Aroyo, M. I. et al. Bilbao Crystallographic Server: I. Databases and crystallographic computing programs. Z. Kristallogr. 221, 15–27 (2006)
Aroyo, M. I., Kirov, A., Capillas, C., Perez-Mato, J. M. & Wondratschek, H. Bilbao Crystallographic Server. II. Representations of crystallographic point groups and space groups. Acta Crystallogr. A62, 115–128 (2006)
Cao, W. Phenomenological theories of ferroelectric phase transitions. Br. Ceram. Trans. 103, 71–75 (2004)
Perdew, J. P. & Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 23, 5048–5079 (1981)
Becke, A. D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 38, 3098–3100 (1988)
Lee, C., Yang, W. & Parr, R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 37, 785–789 (1988)
Stroppa, A. & Kresse, G. The shortcomings of semi-local and hybrid functionals: what we can learn from surface science studies. New J. Phys. 10, 063020 (2008)
Acknowledgements
We acknowledge financial support from the Spanish Ministry of Economy and Competitiveness (FIS2013- 48286-C2-2-P), the EPSRC (UK) (grant numbers EP/J017639/1 and EP/K014560/1), the Cambridge Commonwealth Trust, the National Natural Science Foundation of China (grant numbers 11204111, 11404148, 11274136 and 11534003), the 2012 Changjiang Scholars Program of China, and the Natural Science Foundation of Jiangsu province (grant number BK20130223). C.J.P. acknowledges support from the Royal Society through a Wolfson Research Merit award. Work at Carnegie was supported by EFree, an Energy Frontier Research Center funded by the DOE, Office of Science, Basic Energy Sciences under award number DE-SC-0001057. Computer facilities were provided by PRACE and the Donostia International Physics Center (DIPC).
Author information
Authors and Affiliations
Contributions
I.E., M.C. and F.M. performed the anharmonic and superconducting calculations. All authors contributed to the design of the research project and to the writing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
Extended Data Figure 1 Equations of state.
Pressure P as a function of volume V for the  (left) and R3m (right) phases, calculated from the static energy EBO that represents the classical nuclei limit (black), and including the vibrational contribution within the SSCHA for both H3S (red) and D3S (green).
(left) and R3m (right) phases, calculated from the static energy EBO that represents the classical nuclei limit (black), and including the vibrational contribution within the SSCHA for both H3S (red) and D3S (green).
Extended Data Figure 2 Bond symmetrization within LDA (left) and BLYP (right).
For each volume V the relative coordinate x = (d2 − a/2)/(a/2), in which d2 is the length of the hydrogen bond and a is the lattice parameter, obtained at the energy minimum is given. When x = 0, the covalent and hydrogen bonds have the same length and the structure is fully symmetric. The energy is calculated at the static level without any vibrational contribution as derived from the BOES (black), and including the quantum anharmonic vibrational contribution both for H3S (green) and D3S (purple). The pressure P below which the cubic structure distorts is given in each case.
Extended Data Figure 3 Vibrational energy.
SSCHA anharmonic vibrational energy ( ) calculated as a function of the relative coordinate x = (d2 − a/2)/(a/2) for different volumes (see legend).
) calculated as a function of the relative coordinate x = (d2 − a/2)/(a/2) for different volumes (see legend).
Extended Data Figure 4 Dependence of the equation of state on the density functional.
The equation of state is calculated with different exchange correlation functionals with (right) and without (left) the vibrational contribution to the pressure. At each volume V the pressure P of the structure with minimum energy is given, which depends on whether or not the vibrational contribution is included (see Extended Data Fig. 2). The results are compared with the two curves obtained experimentally10.
Extended Data Figure 5 Phonons of 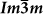 D3S.
D3S.
Comparison between the harmonic and anharmonic phonons of  at two different pressures for D3S: 133 GPa (left) and 155 GPa (right).
at two different pressures for D3S: 133 GPa (left) and 155 GPa (right).
Extended Data Figure 6 Anharmonic phonons of R3m H3S.
Anharmonic phonons are shown at two different pressures: 153 GPa (left) and 133 GPa (right). The Eliashberg functions α2F(ω) are also shown.
Extended Data Figure 7 Superconducting properties of 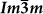 H3S.
H3S.
Anharmonic Eliashberg function α2F(ω) (solid lines) and integrated electron–phonon coupling constant λ(ω) (dashed lines) of the  phase as functions of frequency ω at two different pressures: 135 GPa (black) and 157 GPa (red).
phase as functions of frequency ω at two different pressures: 135 GPa (black) and 157 GPa (red).
Rights and permissions
About this article
Cite this article
Errea, I., Calandra, M., Pickard, C. et al. Quantum hydrogen-bond symmetrization in the superconducting hydrogen sulfide system. Nature 532, 81–84 (2016). https://doi.org/10.1038/nature17175
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature17175
This article is cited by
-
Full-bandwidth anisotropic Migdal-Eliashberg theory and its application to superhydrides
Communications Physics (2024)
-
RETRACTED ARTICLE: Evidence of near-ambient superconductivity in a N-doped lutetium hydride
Nature (2023)
-
Quantum lattice dynamics and their importance in ternary superhydride clathrates
Communications Physics (2023)
-
Excitonic insulator to superconductor phase transition in ultra-compressed helium
Nature Communications (2023)
-
Many-body quantum muon effects and quadrupolar coupling in solids
Communications Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.




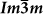 D3S.
D3S.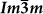 H3S.
H3S.