Abstract
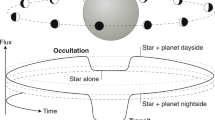
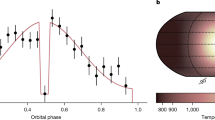
Over the past decade, observations of giant exoplanets (Jupiter-size) have provided key insights into their atmospheres1,2, but the properties of lower-mass exoplanets (sub-Neptune) remain largely unconstrained because of the challenges of observing small planets. Numerous efforts to observe the spectra of super-Earths—exoplanets with masses of one to ten times that of Earth—have so far revealed only featureless spectra3. Here we report a longitudinal thermal brightness map of the nearby transiting super-Earth 55 Cancri e (refs 4, 5) revealing highly asymmetric dayside thermal emission and a strong day–night temperature contrast. Dedicated space-based monitoring of the planet in the infrared revealed a modulation of the thermal flux as 55 Cancri e revolves around its star in a tidally locked configuration. These observations reveal a hot spot that is located 41 ± 12 degrees east of the substellar point (the point at which incident light from the star is perpendicular to the surface of the planet). From the orbital phase curve, we also constrain the nightside brightness temperature of the planet to 1,380 ± 400 kelvin and the temperature of the warmest hemisphere (centred on the hot spot) to be about 1,300 kelvin hotter (2,700 ± 270 kelvin) at a wavelength of 4.5 micrometres, which indicates inefficient heat redistribution from the dayside to the nightside. Our observations are consistent with either an optically thick atmosphere with heat recirculation confined to the planetary dayside, or a planet devoid of atmosphere with low-viscosity magma flows at the surface6.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout


Similar content being viewed by others
References
Burrows, A. S. Highlights in the study of exoplanet atmospheres. Nature 513, 345–352 (2014)
Heng, K. & Showman, A. P. Atmospheric dynamics of hot exoplanets. Annu. Rev. Earth Planet. Sci. 43, 509–540 (2015)
Knutson, H. A. et al. Hubble Space Telescope near-IR transmission spectroscopy of the super-Earth HD 97658b. Astrophys. J. 794, 155 (2014)
Demory, B.-O. et al. Detection of a transit of the super-Earth 55 Cancri e with warm Spitzer. Astron. Astrophys. 533, A114 (2011)
Winn, J. N. et al. A super-Earth transiting a naked-eye star. Astrophys. J. 737, L18 (2011)
Solomatov, V. in Treatise on Geophysics Vol. 9 (ed. Schubert, G. ) 91–119 (Elsevier, 2007)
Demory, B.-O., Gillon, M., Madhusudhan, N. & Queloz, D. Variability in the super-Earth 55 Cnc e. Mon. Not. R. Astron. Soc. 455, 2018–2027 (2016)
Gillon, M. et al. The TRAPPIST survey of southern transiting planets. I. Thirty eclipses of the ultra-short period planet WASP-43 b. Astron. Astrophys. 542, A4 (2012)
Stevenson, K. B. et al. Transit and eclipse analyses of the exoplanet HD 149026b using BLISS mapping. Astrophys. J. 754, 136 (2012)
Lanotte, A. A. et al. A global analysis of Spitzer and new HARPS data confirms the loneliness and metal-richness of GJ 436 b. Astron. Astrophys. 572, A73 (2014)
Deming, D. et al. Spitzer secondary eclipses of the dense, modestly-irradiated, giant exoplanet HAT-P-20b using pixel-level decorrelation. Astrophys. J. 805, 132 (2015)
Pont, F., Zucker, S. & Queloz, D. The effect of red noise on planetary transit detection. Mon. Not. R. Astron. Soc. 373, 231–242 (2006)
Fischer, D. A. et al. Five planets orbiting 55 Cancri. Astrophys. J. 675, 790–801 (2008)
Berta, Z. K. et al. The GJ1214 super-Earth system: stellar variability, new transits, and a search for additional planets. Astrophys. J. 736, 12 (2011)
Mazeh, T. & Faigler, S. Detection of the ellipsoidal and the relativistic beaming effects in the CoRoT-3 lightcurve. Astron. Astrophys. 521, L59 (2010)
Budaj, J. The reflection effect in interacting binaries or in planet–star systems. Astron. J. 141, 59 (2011)
Shkolnik, E., Bohlender, D. A., Walker, G. A. H. & Collier Cameron, A. The on/off nature of star–planet interactions. Astrophys. J. 676, 628–638 (2008)
Miller, B. P., Gallo, E., Wright, J. T. & Pearson, E. G. A comprehensive statistical assessment of star–planet interaction. Astrophys. J. 799, 163 (2015)
de Wit, J., Gillon, M., Demory, B.-O. & Seager, S. Towards consistent mapping of distant worlds: secondary-eclipse scanning of the exoplanet HD 189733b. Astron. Astrophys. 548, A128 (2012)
Demory, B.-O. et al. Inference of inhomogeneous clouds in an exoplanet atmosphere. Astrophys. J. 776, L25 (2013)
Cowan, N. B. et al. Alien maps of an ocean-bearing world. Astrophys. J. 700, 915–923 (2009)
Showman, A. P., Fortney, J. J., Lewis, N. K. & Shabram, M. Doppler signatures of the atmospheric circulation on hot Jupiters. Astrophys. J. 762, 24 (2013)
Gillon, M. et al. Improved precision on the radius of the nearby super-Earth 55 Cnc e. Astron. Astrophys. 539, A28 (2012)
Ehrenreich, D. et al. Hint of a transiting extended atmosphere on 55 Cancri b. Astron. Astrophys. 547, A18 (2012)
Madhusudhan, N. & Seager, S. On the inference of thermal inversions in hot Jupiter atmospheres. Astrophys. J. 725, 261–274 (2010)
Heng, K. & Kopparla, P. On the stability of super-Earth atmospheres. Astrophys. J. 754, 60 (2012)
Schaefer, L. & Fegley, B. Jr. Atmospheric chemistry of Venus-like exoplanets. Astrophys. J. 729, 6 (2011)
Miguel, Y., Kaltenegger, L., Fegley, B. & Schaefer, L. Compositions of hot super-Earth atmospheres: exploring Kepler candidates. Astrophys. J. 742, L19 (2011)
Lutgens, F. K. & Tarbuck, E. J. Essentials of Geology 7th edn, Ch. 3 (Prentice Hall, 2000)
Nelson, B. E. et al. The 55 Cancri planetary system: fully self-consistent N-body constraints and a dynamical analysis. Mon. Not. R. Astron. Soc. 441, 442–451 (2014)
Ballard, S. et al. Kepler-93b: a terrestrial world measured to within 120 km, and a test case for a new Spitzer observing mode. Astrophys. J. 790, 12 (2014)
Eastman, J., Siverd, R. & Gaudi, B. S. Achieving better than 1 minute accuracy in the heliocentric and barycentric Julian Dates. Publ. Astron. Soc. Pacif. 122, 935–946 (2010)
Landsman, W. B. The IDL Astronomy User’s Library. In Astronomical Data Analysis Software and Systems II Vol. 52 of ASP Conf. Ser. (eds Hanisch, R. J. et al.) 246–248 (Astronomical Society of the Pacific, 1993)
Agol, E. et al. The climate of HD 189733b from fourteen transits and eclipses measured by Spitzer. Astrophys. J. 721, 1861–1877 (2010)
Beerer, I. M. et al. Secondary eclipse photometry of wasp-4b with warm spitzer. Astrophys. J. 727, 23 (2011)
Schwarz, G. Estimating the dimension of a model. Ann. Stat. 6, 461–464 (1978)
Sobolev, V. V. Light Scattering in Planetary Atmospheres Vol. 76 of International Series of Monographs in Natural Philosophy Ch. 9 (Pergamon Press, 1975) [transl.]
Mandel, K. & Agol, E. Analytic light curves for planetary transit searches. Astrophys. J. 580, L171–L175 (2002)
Claret, A. & Bloemen, S. Gravity and limb-darkening coefficients for the Kepler, CoRoT, Spitzer, uvby, UBVRIJHK, and Sloan photometric systems. Astron. Astrophys. 529, A75 (2011)
von Braun, K. et al. 55 Cancri: stellar astrophysical parameters, a planet in the habitable zone, and implications for the radius of a transiting super-Earth. Astrophys. J. 740, 49 (2011)
Knutson, H. A. et al. A map of the day–night contrast of the extrasolar planet HD 189733b. Nature 447, 183–186 (2007)
Cowan, N. B. & Agol, E. Inverting phase functions to map exoplanets. Astrophys. J. 678, L129–L132 (2008)
Crossfield, I. J. M. ACME stellar spectra. I. Absolutely calibrated, mostly empirical flux densities of 55 Cancri and its transiting planet 55 Cancri e. Astron. Astrophys. 545, A97 (2012)
Menou, K. Magnetic scaling laws for the atmospheres of hot giant exoplanets. Astrophys. J. 745, 138 (2012)
Owen, J. E. & Wu, Y. Kepler planets: a tale of evaporation. Astrophys. J. 775, 105 (2013)
Bolmont, E., Raymond, S. N., Leconte, J., Hersant, F. & Correia, A. C. M. Mercury-T: a new code to study tidally evolving multi-planet systems. Applications to Kepler-62. Astron. Astrophys. 583, A116 (2015)
Acknowledgements
We thank D. Deming, D. Apai and A. Showman for discussions as well as the Spitzer Science Center staff for their assistance in the planning and executing of these observations. This work is based on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. Support for this work was provided by NASA through an award issued by JPL/Caltech. M.G. is a Research Associate at the Belgian Funds for Scientific Research (FRS-FNRS). V.S. was supported by the Simons Foundation (award number 338555, VS).
Author information
Authors and Affiliations
Contributions
B.-O.D. initiated and led the Spitzer observing programme, conducted the data analysis and wrote the paper. M.G. performed an independent analysis of the dataset. E.B. carried out the simulations assessing the amplitude of tidal heating in the interior of 55 Cancri e. J.d.W. performed the longitudinal mapping of the planet. N.M. wrote the interpretation section with inputs from E.B., K.H., V.S., R.H., N.L. and T.K. J.K., B.B., S.K. and D.Q. contributed to the observing programme. All authors commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
Extended Data Figure 1 55 Cancri e raw photometry.
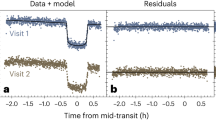
a–c, The raw data for time series acquired on 15 June 2013 (a), 18 June 2013 (b) and 21 June 2013 (c). The best-fit instrumental + astrophysical model is superimposed in red. Grey filled circles are data binned per 30 s. Black filled circles are data binned per 15 min. The error bars are the standard deviation of the mean within each time bin. BJD, barycentric Julian date.
Extended Data Figure 2 Continuation of Extended Data Fig. 1.
a–c, The raw data for time series acquired on 29 June 2013 (a), 3 July 2013 (b) and 8 July 2013 (c).
Extended Data Figure 3 Continuation of Extended Data Fig. 1.
a–c, The raw data for time series acquired on 11 July 2013 (a, b) and 15 July 2013 (c).
Extended Data Figure 4 55 Cancri e corrected photometry.
a–c, The detrended data for time series acquired on 15 June 2013 (a), 18 June 2013 (b) and 21 June 2013 (c). The best-fit instrumental + astrophysical model is superimposed in red. Grey filled circles are data binned per 30 s. Black filled circles are data binned per 15 min. The error bars are the standard deviation of the mean within each time bin. BJD, barycentric Julian date.
Extended Data Figure 5 Continuation of Extended Data Fig. 4.
a–c, The detrended data for time-series acquired on 29 June 2013 (a), 3 July 2013 (b) and 8 July 2013 (c).
Extended Data Figure 6 Continuation of Extended Data Fig. 4.
a–c, The detrended data for time-series acquired on 11 July 2013 (a, b) and 15 July 2013 (c).
Extended Data Figure 7 Photometric r.m.s. versus bin size for all data sets.
a–i, Black filled circles indicate the photometric residual r.m.s. for different time bins. Each panel corresponds to each individual data set (a–i, increasing observing date). The expected decrease in Poisson noise normalized to an individual bin (30 s) precision is shown as a red dotted line.
Extended Data Figure 8 Polynomial-detrended phase-folded photometry.
Photometry for all eight data sets combined and folded on the orbital period of 55 Cancri e. a, Fit results using the entire time series as input data. b, Fit results obtained by splitting the times series in two. Data in a and b represent the planet-to-star flux ratio (Fplanet/Fstar) variation in phase and are binned per 15 min; the error bars are the standard deviation of the mean within each orbital phase bin. The best-fit model is shown in red. Contrary to Fig. 1, these fits are obtained using polynomial functions of the centroid position and the FWHM of the PRF.
Extended Data Figure 9 Tidal heating constraints for 55 Cancri e.
The planet-to-star flux ratio (Fp/F⋆) is shown as a function of the orbital eccentricity for different values of dissipation (relative to the Earth’s σ⊕; indicated by the different colours) and albedos (‘A’, indicated by the different line styles, from 0.0 (solid) to 1.0 (long-dashed)). The pink and orange bands represent the occultation depth values measured in 2012 and 2013 with Spitzer, respectively. Vertical lines indicate the plausible range of the eccentricity of 55 Cancri e as determined from the N-body simulations for each dissipation value. The 2012 occultation depth can be matched for high albedos and a high dissipation, while the deeper 2013 occultation depth can be matched for the highest dissipation (10σ⊕) and the whole albedo range.
PowerPoint slides
Rights and permissions
About this article
Cite this article
Demory, BO., Gillon, M., de Wit, J. et al. A map of the large day–night temperature gradient of a super-Earth exoplanet. Nature 532, 207–209 (2016). https://doi.org/10.1038/nature17169
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature17169
This article is cited by
-
Dynamics and clouds in planetary atmospheres from telescopic observations
The Astronomy and Astrophysics Review (2023)
-
Measured spin–orbit alignment of ultra-short-period super-Earth 55 Cancri e
Nature Astronomy (2022)
-
Detectability of Rocky-Vapour atmospheres on super-Earths with Ariel
Experimental Astronomy (2022)
-
The search for living worlds and the connection to our cosmic origins
Experimental Astronomy (2022)
-
Disentangling atmospheric compositions of K2-18 b with next generation facilities
Experimental Astronomy (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.