Abstract
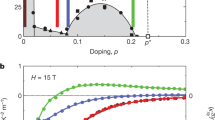
The pseudogap is a partial gap in the electronic density of states that opens in the normal (non-superconducting) state of cuprate superconductors and whose origin is a long-standing puzzle. Its connection to the Mott insulator phase at low doping (hole concentration, p) remains ambiguous1 and its relation to the charge order2,3,4 that reconstructs the Fermi surface5,6 at intermediate doping is still unclear7,8,9,10. Here we use measurements of the Hall coefficient in magnetic fields up to 88 tesla to show that Fermi-surface reconstruction by charge order in the cuprate YBa2Cu3Oy ends sharply at a critical doping p = 0.16 that is distinctly lower than the pseudogap critical point p* = 0.19 (ref. 11). This shows that the pseudogap and charge order are separate phenomena. We find that the change in carrier density n from n = 1 + p in the conventional metal at high doping (ref. 12) to n = p at low doping (ref. 13) starts at the pseudogap critical point. This shows that the pseudogap and the antiferromagnetic Mott insulator are linked.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Norman, M. R., Pines, D. & Kallin, C. The pseudogap: friend or foe of high Tc? Adv. Phys. 54, 715–733 (2005)
Wu, T. et al. Magnetic-field-induced charge-stripe order in the high-temperature superconductor YBa2Cu3Oy . Nature 477, 191–194 (2011)
Ghiringhelli, G. et al. Long-range incommensurate charge fluctuations in (Y,Nd)Ba2Cu3O6+x . Science 337, 821–825 (2012)
Chang, J. et al. Direct observation of competition between superconductivity and charge density wave order in YBa2Cu3O6.67 . Nature Phys . 8, 871–876 (2012)
Doiron-Leyraud, N. et al. Quantum oscillations and the Fermi surface in an underdoped high-Tc superconductor. Nature 447, 565–568 (2007)
LeBoeuf, D. et al. Lifshitz critical point in the cuprate superconductor YBa2Cu3Oy from high-field Hall effect measurements. Phys. Rev. B 83, 054506 (2011)
He, Y. et al. Fermi surface and pseudogap evolution in a cuprate superconductor. Science 344, 608–611 (2014)
Fujita, K. et al. Simultaneous transitions in cuprate momentum-space topology and electronic symmetry breaking. Science 344, 612–616 (2014)
Ramshaw, B. J. et al. Quasiparticle mass enhancement approaching optimal doping in a high-Tc superconductor. Science 348, 317–320 (2015)
Senthil, T. On the mass enhancement near optimal doping in high magnetic fields in the cuprates. Preprint at http://arXiv.org/abs/1410.2096 (2014)
Tallon, J. L. & Loram, J. W. The doping dependence of T* — what is the real high-Tc phase diagram? Physica C 349, 53–68 (2001)
Mackenzie, A. P. et al. Normal-state magnetotransport in superconducting Ta2Ba2CuO6+δ to millikelvin temperatures. Phys. Rev. B 53, 5848–5855 (1996)
Ando, Y. et al. Evolution of the Hall coefficient and the peculiar electronic structure of the cuprate superconductors. Phys. Rev. Lett. 92, 197001 (2004)
Vignolle, B. et al. Quantum oscillations in an overdoped high-Tc superconductor. Nature 455, 952–955 (2008)
Hussey, N. E. Phenomenology of the normal state in-plane transport properties of high-Tc cuprates. J. Phys. Condens. Matter 20, 123201 (2008)
Segawa, K. & Ando, Y. Intrinsic Hall response of the CuO2 planes in a chain-plane composite system of YBa2Cu3Oy . Phys. Rev. B 69, 104521 (2004)
Balakirev, F. F. et al. Quantum phase transition in the magnetic-field-induced normal state of optimum-doped high-Tc cuprate superconductors at low temperatures. Phys. Rev. Lett. 102, 017004 (2009)
Yoshida, T. et al. Systematic doping evolution of the underlying Fermi surface of La2-xSrxCuO4 . Phys. Rev. B 74, 224510 (2006)
Croft, T. P., Lester, C., Senn, M. S., Bombardi, A. & Hayden, S. M. Charge density wave fluctuations in La2-xSrxCuO4 and their competition with superconductivity. Phys. Rev. B 89, 224513 (2014)
Balakirev, F. F. et al. Signature of optimal doping in Hall-effect measurements on a high-temperature superconductor. Nature 424, 912–915 (2003)
Fournier, D. et al. Loss of nodal quasiparticle integrity in underdoped YBa2Cu3O6+x . Nature Phys . 6, 905–911 (2010)
Hücker, M. et al. Competing charge, spin and superconducting orders in underdoped YBa2Cu3Oy . Phys. Rev. B 90, 054514 (2014)
Blanco-Canosa, S. et al. Resonant X-ray scattering study of charge-density wave correlations in YBa2Cu3O6+x . Phys. Rev. B 90, 054513 (2014)
Wu, T. et al. Emergence of charge order from the vortex state of a high-temperature superconductor. Nature Commun . 4, 2113 (2013)
Tallon, J. L. et al. Zn-induced Tc reduction in high-Tc superconductors: scattering in the presence of a pseudogap. Phys. Rev. Lett. 79, 5294–5297 (1997)
Blanco-Canosa, S. et al. Momentum-dependent charge correlations in YBa2Cu3O6+δ superconductors probed by resonant X-ray scattering: evidence for three competing phases. Phys. Rev. Lett. 110, 187001 (2013)
Dagan, Y. et al. Evidence for a quantum phase transition in Pr2-xCexCuO4-δ from transport measurements. Phys. Rev. Lett. 92, 167001 (2004)
Haug, D. et al. Neutron scattering study of the magnetic phase diagram of underdoped YBa2Cu3O6+x . New J. Phys. 12, 105006 (2010)
Taillefer, L. Scattering and pairing in cuprate superconductors. Annu. Rev. Condens. Matter Phys. 1, 51–70 (2010)
Sénéchal, D. & Tremblay, A.-M. S. Hot spots and pseudogaps for hole- and electron-doped high-temperature superconductors. Phys. Rev. Lett. 92, 126401 (2004)
Ferrero, M. et al. Pseudogap opening and formation of Fermi arcs as an orbital-selective Mott transition in momentum space. Phys. Rev. B 80, 064501 (2009)
Rice, T. M. et al. A phenomenological theory of the anomalous pseudogap phase in underdoped cuprates. Rep. Prog. Phys. 75, 016502 (2012)
Chowdhury, D. & Sachdev, S. Density-wave instabilities of fractionalized Fermi liquids. Phys. Rev. B 90, 245136 (2014)
Liang, R., Bonn, D. A. & Hardy, W. N. Growth of YBCO single crystals by the self-flux technique. Phil. Mag. 92, 2563–2581 (2012)
Liang, R., Bonn, D. A. & Hardy, W. N. Evaluation of CuO2 plane hole doping in YBa2Cu3O6+x single crystals. Phys. Rev. B 73, 180505 (2006)
Gagnon, R., Lupien, C. & Taillefer, L. T2 dependence of the resistivity in the CuO chains of YBa2Cu3O6.9 . Phys. Rev. B 50, 3458–3461 (1994)
Hussey, N. The normal state scattering rate in high-Tc cuprates. Eur. Phys. J. B 31, 495–507 (2003)
Manako, T. et al. Transport and structural study of Tl2Ba2CuO6+δ single crystals prepared by the KCl flux method. Phys. Rev. B 46, 11019–11024 (1992)
Hussey, N. E. et al. Angular dependence of the c-axis normal-state magnetoresistance in single crystal Tl2Ba2CuO6 . Phys. Rev. Lett. 76, 122–125 (1996)
Acknowledgements
We thank the following for discussions: Y. Ando, D. Basov, G. Boebinger, C. Bourbonnais, J. P. Carbotte, A. Carrington, J. Chang, A. V. Chubukov, J. C. Davis, A. Georges, N. E. Hussey, M.-H. Julien, H.-Y. Kee, S. A. Kivelson, P. A. Lee, T. Loew, G. G. Lonzarich, W. Metzner, A. J. Millis, M. R. Norman, C. Pépin, J. Porras, B. J. Ramshaw, T. M. Rice, G. Rikken, S. Sachdev, D. J. Scalapino, C. B. Taillefer, J. L. Tallon, S. Todadri, and A.-M. S. Tremblay. We also thank P. Frings and J.P. Nicolin for help during the measurements in Toulouse. L.T. thanks the Laboratoire National des Champs Magnétiques Intenses (LNCMI) in Toulouse for their hospitality and LABEX NEXT for their support while this work was being performed. A portion of this work was performed at the LNCMI, which is supported by the French ANR SUPERFIELD, the EMFL, and the LABEX NEXT. R.L., D.A.B. and W.N.H. acknowledge funding from the Natural Sciences and Engineering Research Council of Canada (NSERC). L.T. acknowledges support from the Canadian Institute for Advanced Research (CIFAR) and funding from NSERC, the Fonds de recherche du Québec – Nature et Technologies (FRQNT), the Canada Foundation for Innovation (CFI) and a Canada Research Chair.
Author information
Authors and Affiliations
Contributions
S.B., W.T., F.L., B.V., D.V., J.B. and C.P. performed the transport measurements at the LNCMI. S.B. and N.D.-L. performed the transport measurements at Sherbrooke. G.G. performed the calculations of the transport coefficients. D.A.B., W.N.H. and R.L. prepared the YBCO single crystals at UBC. S.B., L.T. and C.P. wrote the manuscript, in consultation with all authors. L.T. and C.P. co-supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
Extended Data Figure 1 Temperature dependence of resistivity of CuO chains in YBCO at p = 0.177.
Shown is the chain resistivity in YBCO at p = 0.177 (red), defined as ρchain = 1/[(1/ρb) − (1/ρa)], where ρa and ρb are the in-plane resistivities along the a and b directions of the orthorhombic structure, respectively, plotted versus T2. The black line is a linear fit that extrapolates to ρchain = 50 μΩ cm at T = 50 K.
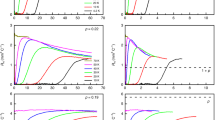
Extended Data Figure 2 Isotherms of RH versus H in YBCO at p = 0.16.
Shown is the magnetic field dependence of the Hall coefficient RH in our YBCO sample with y = 6.92 (Tc = 93.5 K; p = = 0.161) at various temperatures, as indicated (key at right).
Extended Data Figure 3 Isotherms of RH versus H in YBCO at p = 0.177.
As for Extended Data Fig. 2 but for our YBCO sample with y = 6.97 (Tc = 91 K; p = 0.177).
Extended Data Figure 4 Isotherms of RH versus H in YBCO at p = 0.19.
As for Extended Data Fig. 2 but for our YBCO sample with y = 6.99 and 1.4% Ca doping (Tc = 87 K; p = 0.19).
Extended Data Figure 5 Isotherms of RH versus H in YBCO at p = 0.205.
As for Extended Data Fig. 2 but for our YBCO sample with y = 6.99 and 5% Ca doping (Tc = 77 K; p = 0.205).
Extended Data Figure 6 Doping dependence of Tmax.
Shown is the temperature Tmax at which RH versus T peaks in YBCO (Fig. 3a), plotted versus doping p. At p = 0.16, there is no downturn in the normal-state RH(T) down to 40 K. The p = 0.16 data are consistent with Tmax = 0 (lower bound), with an upper bound at Tmax = 40 K (shown as black vertical segment). The width of the grey band marks the upper and lower limits for Tmax versus p. The green diamond defines the critical doping above which FSR is no longer present, at pFSR = 0.16 ± 0.005, with an error bar defined from the minimal and maximal possible values of Tmax. Error bars on the three data points (black dots) represent the uncertainty in defining the peak position of the RH(T) curves in Fig. 3a.
Extended Data Figure 7 Zoom on RH versus T in Tl-2201 and YBCO at high doping.
a, Temperature dependence of RH in Tl-2201 (squares) at p = 0.3 (blue, Tc = 10 K; ref. 38) and p = 0.27 (green, Tc = 25 K; ref. 39). b, RH versus T in YBCO (circles, from Extended Data Figs 4, 5 and 8) at p = 0.205 (yellow) and p = 0.19 (blue). The dashed lines are an extrapolation of the low-T data to T = 0. The YBCO curve at p = 0.205 is qualitatively similar to the two Tl-2201 curves, all exhibiting an initial rise with increasing temperature from T = 0, and a characteristic peak at T ≈ 100 K—two features attributed to inelastic scattering on a large hole-like Fermi surface15. The YBCO curve at p = 0.19 is qualitatively different, showing no sign of a drop at low T (see Extended Data Fig. 8). We attribute the twofold increase in the magnitude of RH at T → 0 to a decrease in carrier density as the pseudogap opens at p*, with p* located between p = 0.205 and p = 0.19. The error bars are defined in the legend of Fig. 3.
Extended Data Figure 8 Comparison between p = 0.205 and p = 0.19.
a, b, The field dependence of the Hall coefficient RH in YBCO at p = 0.205 (a) and p = 0.19 (b), for different temperatures as indicated. The colour-coded lines are parallel linear fits to the high-field data. They show that at low temperature RH decreases upon cooling at p = 0.205, while it saturates at p = 0.19. The value of RH given by the fit line, at H = 80 T, is plotted in Fig. 3 and in Extended Data Fig. 7b. Similar fits are used to extract RH(80 T) for p = 0.16 and p = 0.177 (from data in Extended Data Figs 2 and 3).
Extended Data Figure 9 Scenario of inelastic scattering.
a, RH versus T in YBCO at four dopings p, as indicated (Fig. 3b). b, Electrical resistivity ρa versus T in YBCO at four dopings, as indicated. Lines are at H = 0; dots are in the normal state at high field. c, RH versus T calculated for five values of inelastic scattering, with Γ1 = 0, 1, 5, 15 and 25 THz K−1, showing that RH(T) grows with increasing Γ1 (see Methods). Dots are from a. d, Corresponding calculated values of the electrical resistivity ρa, plotted versus T, using the same parameters and values of Γ1 as for the colour-coded curves of c. The vertical grey lines mark T = 50 K, the temperature at which we see a sixfold increase in RH (a), yet no increase in ρa (b). The calculation can reproduce the large increase in RH (c), but it is accompanied by a tenfold increase in ρa (d).
Extended Data Figure 10 Magnetic field profile.
Time dependence of the magnetic field pulse in the 90 T dual-coil magnet at the LNCMI in Toulouse. Inset, zoom around maximum field.
Rights and permissions
About this article
Cite this article
Badoux, S., Tabis, W., Laliberté, F. et al. Change of carrier density at the pseudogap critical point of a cuprate superconductor. Nature 531, 210–214 (2016). https://doi.org/10.1038/nature16983
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature16983
This article is cited by
-
Low-Field Hall effect, Pseudogap and Magnetic Textures in the Bi\(_{2}\)Sr\(_{2}\)CaCu\(_{2}\)O\(_{8+x}\) Superconductor
Journal of Superconductivity and Novel Magnetism (2024)
-
Theoretical understanding of correlation between magnetic phase transition and the superconducting dome in high-Tc cuprates
Science China Physics, Mechanics & Astronomy (2024)
-
Reconciling scaling of the optical conductivity of cuprate superconductors with Planckian resistivity and specific heat
Nature Communications (2023)
-
Pseudogap behavior in charge density wave kagome material ScV6Sn6 revealed by magnetotransport measurements
npj Quantum Materials (2023)
-
Transport properties and doping evolution of the Fermi surface in cuprates
Scientific Reports (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.