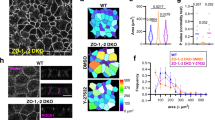
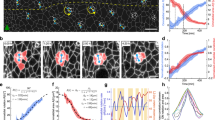
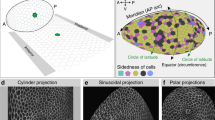
Abstract
The orientation of cell division along the long axis of the interphase cell—the century-old Hertwig’s rule—has profound roles in tissue proliferation, morphogenesis, architecture and mechanics1,2. In epithelial tissues, the shape of the interphase cell is influenced by cell adhesion, mechanical stress, neighbour topology, and planar polarity pathways3,4,5,6,7,8,9,10,11,12. At mitosis, epithelial cells usually adopt a rounded shape to ensure faithful chromosome segregation and to promote morphogenesis1. The mechanisms underlying interphase cell shape sensing in tissues are therefore unknown. Here we show that in Drosophila epithelia, tricellular junctions (TCJs) localize force generators, pulling on astral microtubules and orienting cell division via the Dynein-associated protein Mud independently of the classical Pins/Gαi pathway. Moreover, as cells round up during mitosis, TCJs serve as spatial landmarks, encoding information about interphase cell shape anisotropy to orient division in the rounded mitotic cell. Finally, experimental and simulation data show that shape and mechanical strain sensing by the TCJs emerge from a general geometric property of TCJ distributions in epithelial tissues. Thus, in addition to their function as epithelial barrier structures, TCJs serve as polarity cues promoting geometry and mechanical sensing in epithelial tissues.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Cadart, C., Zlotek-Zlotkiewicz, E., Le Berre, M., Piel, M. & Matthews, H. K. Exploring the function of cell shape and size during mitosis. Dev. Cell 29, 159–169 (2014)
Hertwig, O. Das Problem der Befruchtung und der Isotropie des Eies, eine Theory der Vererbung. Jenaische Zeitschrift fuer Naturwissenschaft. (1884)
Baena-López, L. A., Baonza, A. & García-Bellido, A. The orientation of cell divisions determines the shape of Drosophila organs. Curr. Biol. 15, 1640–1644 (2005)
Saburi, S. et al. Loss of Fat4 disrupts PCP signaling and oriented cell division and leads to cystic kidney disease. Nature Genet. 40, 1010–1015 (2008)
Aigouy, B. et al. Cell flow reorients the axis of planar polarity in the wing epithelium of Drosophila. Cell 142, 773–786 (2010)
Gibson, W. T. et al. Control of the mitotic cleavage plane by local epithelial topology. Cell 144, 427–438 (2011)
Mao, Y. et al. Planar polarization of the atypical myosin Dachs orients cell divisions in Drosophila. Genes Dev. 25, 131–136 (2011)
Campinho, P. et al. Tension-oriented cell divisions limit anisotropic tissue tension in epithelial spreading during zebrafish epiboly. Nature Cell Biol. 15, 1405–1414 (2013)
LeGoff, L., Rouault, H. & Lecuit, T. A global pattern of mechanical stress polarizes cell divisions and cell shape in the growing Drosophila wing disc. Development 140, 4051–4059 (2013)
Mao, Y. et al. Differential proliferation rates generate patterns of mechanical tension that orient tissue growth. EMBO J. 32, 2790–2803 (2013)
Xiong, F. et al. Interplay of cell shape and division orientation promotes robust morphogenesis of developing epithelia. Cell 159, 415–427 (2014)
Wyatt, T. P. et al. Emergence of homeostatic epithelial packing and stress dissipation through divisions oriented along the long cell axis. Proc. Natl Acad. Sci. USA 112, 5726–5731 (2015)
Bosveld, F. et al. Mechanical control of morphogenesis by Fat/Dachsous/Four-jointed planar cell polarity pathway. Science 336, 724–727 (2012)
Kotak, S. & Gönczy, P. Mechanisms of spindle positioning: cortical force generators in the limelight. Curr. Opin. Cell Biol. 25, 741–748 (2013)
Schulte, J. et al. Gliotactin and Discs large form a protein complex at the tricellular junction of polarized epithelial cells in Drosophila. J. Cell Sci. 119, 4391–4401 (2006)
Grill, S. W., Gönczy, P., Stelzer, E. H. & Hyman, A. A. Polarity controls forces governing asymmetric spindle positioning in the Caenorhabditis elegans embryo. Nature 409, 630–633 (2001)
Théry, M., Jiménez-Dalmaroni, A., Racine, V., Bornens, M. & Jülicher, F. Experimental and theoretical study of mitotic spindle orientation. Nature 447, 493–496 (2007)
Minc, N., Burgess, D. & Chang, F. Influence of cell geometry on division-plane positioning. Cell 144, 414–426 (2011)
Morelli, L. G., Uriu, K., Ares, S. & Oates, A. C. Computational approaches to developmental patterning. Science 336, 187–191 (2012)
Fink, J. et al. External forces control mitotic spindle positioning. Nature Cell Biol. 13, 771–778 (2011)
Kwon, M., Bagonis, M., Danuser, G. & Pellman, D. Direct microtubule-binding by myosin-10 orients centrosomes toward retraction fibers and subcortical actin clouds. Dev. Cell 34, 323–337 (2015)
Tamada, M. & Zallen, J. A. Square cell packing in the Drosophila embryo through spatiotemporally regulated EGF receptor signaling. Dev. Cell 35, 151–161 (2015)
Machicoane, M. et al. SLK-dependent activation of ERMs controls LGN-NuMA localization and spindle orientation. J. Cell Biol. 205, 791–799 (2014)
Byri, S. et al. The triple-repeat protein anakonda controls epithelial tricellular junction formation in Drosophila. Dev. Cell 33, 535–548 (2015)
Furuse, M., Izumi, Y., Oda, Y., Higashi, T. & Iwamoto, N. Molecular organization of tricellular tight junctions. Tissue Barriers 2, e28960 (2014)
Lye, C. M., Naylor, H. W. & Sanson, B. Subcellular localisations of the CPTI collection of YFP-tagged proteins in Drosophila embryos. Development 141, 4006–4017 (2014)
Rauskolb, C., Pan, G., Reddy, B. V., Oh, H. & Irvine, K. D. Zyxin links fat signaling to the hippo pathway. PLoS Biol. 9, e1000624 (2011)
Sawyer, J. K., Harris, N. J., Slep, K. C., Gaul, U. & Peifer, M. The Drosophila afadin homologue Canoe regulates linkage of the actin cytoskeleton to adherens junctions during apical constriction. J. Cell Biol. 186, 57–73 (2009)
Oda, Y., Otani, T., Ikenouchi, J. & Furuse, M. Tricellulin regulates junctional tension of epithelial cells at tricellular contacts through Cdc42. J. Cell Sci. 127, 4201–4212 (2014)
Allen, M. J. et al. Targeted expression of truncated glued disrupts giant fiber synapse formation in Drosophila. J. Neurosci. 19, 9374–9384 (1999)
Herszterg, S., Leibfried, A., Bosveld, F., Martin, C. & Bellaiche, Y. Interplay between the dividing cell and its neighbors regulates adherens junction formation during cytokinesis in epithelial tissue. Dev. Cell 24, 256–270 (2013)
Xu, T. & Rubin, G. M. Analysis of genetic mosaics in developing and adult Drosophila tissues. Development 117, 1223–1237 (1993)
Lee, T. & Luo, L. Mosaic analysis with a repressible cell marker for studies of gene function in neuronal morphogenesis. Neuron 22, 451–461 (1999)
Nakajima, Y., Meyer, E. J., Kroesen, A., McKinney, S. A. & Gibson, M. C. Epithelial junctions maintain tissue architecture by directing planar spindle orientation. Nature 500, 359–362 (2013)
Venken, K. J., He, Y., Hoskins, R. A. & Bellen, H. J. P[acman]: a BAC transgenic platform for targeted insertion of large DNA fragments in D. melanogaster. Science 314, 1747–1751 (2006)
Venken, K. J. et al. Versatile P[acman] BAC libraries for transgenesis studies in Drosophila melanogaster. Nature Methods 6, 431–434 (2009)
Warming, S., Costantino, N., Court, D. L., Jenkins, N. A. & Copeland, N. G. Simple and highly efficient BAC recombineering using galK selection. Nucleic Acids Res. 33, e36 (2005)
Venken, K. J. et al. Recombineering-mediated tagging of Drosophila genomic constructs for in vivo localization and acute protein inactivation. Nucleic Acids Res. 36, e114 (2008)
Gratz, S. J. et al. Genome engineering of Drosophila with the CRISPR RNA-guided Cas9 nuclease. Genetics 194, 1029–1035 (2013)
Ren, X. et al. Optimized gene editing technology for Drosophila melanogaster using germ line-specific Cas9. Proc. Natl Acad. Sci. USA 110, 19012–19017 (2013)
Gratz, S. J. et al. Highly specific and efficient CRISPR/Cas9-catalyzed homology-directed repair in Drosophila. Genetics 196, 961–971 (2014)
Ségalen, M. et al. The Fz-Dsh planar cell polarity pathway induces oriented cell division via Mud/NuMA in Drosophila and zebrafish. Dev. Cell 19, 740–752 (2010)
Yu, J. X., Guan, Z. & Nash, H. A. The mushroom body defect gene product is an essential component of the meiosis II spindle apparatus in Drosophila oocytes. Genetics 173, 243–253 (2006)
Auld, V. J., Fetter, R. D., Broadie, K. & Goodman, C. S. Gliotactin, a novel transmembrane protein on peripheral glia, is required to form the blood-nerve barrier in Drosophila. Cell 81, 757–767 (1995)
Lamb, R. S., Ward, R. E., Schweizer, L. & Fehon, R. G. Drosophila coracle, a member of the protein 4.1 superfamily, has essential structural functions in the septate junctions and developmental functions in embryonic and adult epithelial cells. Mol. Biol. Cell 9, 3505–3519 (1998)
David, N. B. et al. Drosophila Ric-8 regulates Galphai cortical localization to promote Galphai-dependent planar orientation of the mitotic spindle during asymmetric cell division. Nature Cell Biol. 7, 1083–1090 (2005)
Boulanger, J. et al. Patch-based nonlocal functional for denoising fluorescence microscopy image sequences. IEEE Trans. Med. Imaging 29, 442–454 (2010)
Bardet, P. L. et al. PTEN controls junction lengthening and stability during cell rearrangement in epithelial tissue. Dev. Cell 25, 534–546 (2013)
Käfer, J., Hayashi, T., Marée, A. F., Carthew, R. W. & Graner, F. Cell adhesion and cortex contractility determine cell patterning in the Drosophila retina. Proc. Natl Acad. Sci. USA 104, 18549–18554 (2007)
Graner, F. & Glazier, J. Simulation of biological cell sorting using a two-dimensional extended Potts model. Phys. Rev. Lett. 69, 2013–2016 (1992)
Jiang, Y., Swart, P. J., Saxena, A. & Asipauskas, M. & Glazier, J. A. Hysteresis and avalanches in two-dimensional foam rheology simulations. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics 59, 5819–5832 (1999)
Raufaste, C., Dollet, B., Cox, S., Jiang, Y. & Graner, F. Yield drag in a two-dimensional foam flow around a circular obstacle: effect of liquid fraction. Eur. Phys. J. E. Soft Matter 23, 217–228 (2007)
Bonnet, I. et al. Mechanical state, material properties and continuous description of an epithelial tissue. J. R. Soc. Interface 9, 2614–2623 (2012)
Wühr, M., Tan, E. S., Parker, S. K., Detrich, H. W. & Mitchison, T. J. A model for cleavage plane determination in early amphibian and fish embryos. Curr. Biol. 20, 2040–2045 (2010)
Zielke, N. et al. Fly-FUCCI: a versatile tool for studying cell proliferation in complex tissues. Cell Rep. 7, 588–598 (2014)
Bergstralh, D. T., Lovegrove, H. E. & St Johnston, D. Discs large links spindle orientation to apical-basal polarity in Drosophila epithelia. Curr. Biol. 23, 1707–1712 (2013)
Morin, X. & Bellaïche, Y. Mitotic spindle orientation in asymmetric and symmetric cell divisions during animal development. Dev. Cell 21, 102–119 (2011)
Bowman, S. K., Neumüller, R. A., Novatchkova, M., Du, Q. & Knoblich, J. A. The Drosophila NuMA homolog Mud regulates spindle orientation in asymmetric cell division. Dev. Cell 10, 731–742 (2006)
Izumi, Y., Ohta, N., Hisata, K., Raabe, T. & Matsuzaki, F. Drosophila Pins-binding protein Mud regulates spindle-polarity coupling and centrosome organization. Nature Cell Biol. 8, 586–593 (2006)
Siller, K. H., Cabernard, C. & Doe, C. Q. The NuMA-related Mud protein binds Pins and regulates spindle orientation in Drosophila neuroblasts. Nature Cell Biol. 8, 594–600 (2006)
Acknowledgements
We thank V. Auld, A. Bardin, R. Basto, B. Edgar, S. Luschnig, F. Schweisguth, the Bloomington Stock Center and Developmental Studies Hybridoma Bank for reagents; M. Manil-Ségalen, S. Rigaud. T. Piolot and I. Bonnet for input and data analyses; the Developmental Biology Curie imaging facility (PICT-IBiSA@BDD); F. Graner, A. Guichet, S. Herszterg, J.-L. Maître, M. Piel and M. Thery for comments; CePoDro ANR, MorphoDro ERC Advanced, ARC (SL220130607097), Curie Mayent-Rothschild, Labex DEEP, NSF DMR1056456 and ICAM grants for funding.
Author information
Authors and Affiliations
Contributions
F.B., N.M. and Y.B. designed the project. F.B., M.B., A.A. and N.C. performed experiments. C.M., Z.W. and I.G. produced reagents. O.M., B.G., A.P. and N.M. developed methods and scripts for data analysis. O.M. performed simulations. F.B., O.M., B.G., A.P., N.M. and Y.B. analysed the data. D.K.L. and N.M. developed theoretical models. F.B., O.M., D.K.L., N.M. and Y.B. wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
Extended Data Figure 1 Mud, Pins, Gαi and Gli localization during symmetric epithelial cell division in the Drosophila notum.
a, b, Within the Drosophila pupal notum tissue cells divide according to their intephasic cell shape long axis, thereby following the 130-year-old Hertwig rule. However, upon entry into mitosis cells round up (the cell shown in a, −15 to −2 min and Fig. 3b). a, Time-lapse images of Dlg–GFP in a dividing cell (out of 249 cells quantified in b) in the pupal notum tissue illustrating cell rounding during mitosis (the same cell is shown as inset in Fig. 3b). Prior to mitosis (−30 min) the cell (marked by asterisk) is clearly elongated and divides according to its interphasic cell shape (5 min). Upon entry into mitosis (−15 min) the cell rounds up and reaches a minimal anisotropy just before anaphase (−2 min, see also Fig. 3b). b, Rose plot of the difference between the experimental ( ) and predicted division orientations by the average (60–30 min before mitosis) interphase cell long axis (
) and predicted division orientations by the average (60–30 min before mitosis) interphase cell long axis ( ). The data are duplicated relative to 0° line (light green). Number of cells (n) analysed is indicated. c–e, Gαi localization in fixed epithelial dorsal thorax tissue (c), Pins–YFP localization in pins mutant tissue (d) and GFP–Mud localization (e) showing cells in G2 interphase (left) and mitosis (right). Gαi is hardly detected at the cell cortex in G2 phase and is mostly homogenously distributed around the cortex during mitosis. Pins–YFP is homogenously distributed around the cell cortex in both interphase and mitotic cells. In mitosis Pins–YFP also weakly localizes at the mitotic spindle. GFP–Mud localizes at TCJs during interphase and mitosis (see also f). n = 24 cells (c, left); n = 19 cells (c, right); n = 80 cells (d, left); n = 12 cells (d, right); n = 111 cells (e, left) and 54 cells (e, right). f, GFP–Mud time-lapse images from G2 interphase to telophase (n = 21 cells). White arrows, GFP–Mud at TCJs (numbered at t = −22 min). Red and yellow arrowheads, GFP–Mud on the spindle and its poles, respectively. The same panels −22 min to 4 min are shown in Fig. 1a. See also Supplementary Video 1. g, Apical–basal (AB) sections of the cell in f at t = −22 min (top) and t = −1 min (bottom). White arrows, GFP–Mud at TCJs. n = 21 cells. h, GFP–Mud kymograph along the cortex (x axis) from t = −22 to t = 0 min of the cell in f. TCJs numbered as in f. The kymograph shows that during mitotic rounding GFP–Mud spread only modestly along the cortex of the dividing cell. n = 21 cells. i, AB sections of GFP–Mud, adherens junction marker E-Cad and septate junction marker Dlg (top, n = 16 cells) or septate TCJ marker Gli (bottom, n = 30 cells). j–m, Localizations of GFP–Mud (white in j–m and green in j′′–m′′) and Gli (white in j′–m′ and red in j′′–m′′) in fixed pupal wing (j, k) and larval wing disc (l, m) tissues. GFP–Mud co-localizes with Gli at TCJs in G2 interphase and mitotic cells in both the pupal wing and larval wing disc epithelium. Asterisks mark Mud punctate structures present on the nuclear envelope of early G1 cells. Yellow arrows indicate GFP–Mud on the spindle poles. n = 20 cells (j, j′′); n = 5 cells (k, k′′); n = 63 cells (l, l′′) and n = 12 cells (m–m′′). n, o, Localizations of Mud (white in n, o and green in n′′, o′′) and Gli (white in n′, o′ and red in n′′, o′′) detected by antibody staining in G2 interphase and mitotic cells in the pupal dorsal thorax tissue. As observed for GFP–Mud (Fig. 1b and Extended data Fig. 1j–m), the endogenous Mud is enriched at TCJ where it co-localizes with Gli in G2 interphase and mitotic cells. Yellow arrows indicate Mud on the spindle poles. n = 37 cells (n, n′′) and n = 21 cells (o, o′′). Scale bars, 1 μm (a, c, d–g, i, j, k, l, m, n, o), 3 min (h).
). The data are duplicated relative to 0° line (light green). Number of cells (n) analysed is indicated. c–e, Gαi localization in fixed epithelial dorsal thorax tissue (c), Pins–YFP localization in pins mutant tissue (d) and GFP–Mud localization (e) showing cells in G2 interphase (left) and mitosis (right). Gαi is hardly detected at the cell cortex in G2 phase and is mostly homogenously distributed around the cortex during mitosis. Pins–YFP is homogenously distributed around the cell cortex in both interphase and mitotic cells. In mitosis Pins–YFP also weakly localizes at the mitotic spindle. GFP–Mud localizes at TCJs during interphase and mitosis (see also f). n = 24 cells (c, left); n = 19 cells (c, right); n = 80 cells (d, left); n = 12 cells (d, right); n = 111 cells (e, left) and 54 cells (e, right). f, GFP–Mud time-lapse images from G2 interphase to telophase (n = 21 cells). White arrows, GFP–Mud at TCJs (numbered at t = −22 min). Red and yellow arrowheads, GFP–Mud on the spindle and its poles, respectively. The same panels −22 min to 4 min are shown in Fig. 1a. See also Supplementary Video 1. g, Apical–basal (AB) sections of the cell in f at t = −22 min (top) and t = −1 min (bottom). White arrows, GFP–Mud at TCJs. n = 21 cells. h, GFP–Mud kymograph along the cortex (x axis) from t = −22 to t = 0 min of the cell in f. TCJs numbered as in f. The kymograph shows that during mitotic rounding GFP–Mud spread only modestly along the cortex of the dividing cell. n = 21 cells. i, AB sections of GFP–Mud, adherens junction marker E-Cad and septate junction marker Dlg (top, n = 16 cells) or septate TCJ marker Gli (bottom, n = 30 cells). j–m, Localizations of GFP–Mud (white in j–m and green in j′′–m′′) and Gli (white in j′–m′ and red in j′′–m′′) in fixed pupal wing (j, k) and larval wing disc (l, m) tissues. GFP–Mud co-localizes with Gli at TCJs in G2 interphase and mitotic cells in both the pupal wing and larval wing disc epithelium. Asterisks mark Mud punctate structures present on the nuclear envelope of early G1 cells. Yellow arrows indicate GFP–Mud on the spindle poles. n = 20 cells (j, j′′); n = 5 cells (k, k′′); n = 63 cells (l, l′′) and n = 12 cells (m–m′′). n, o, Localizations of Mud (white in n, o and green in n′′, o′′) and Gli (white in n′, o′ and red in n′′, o′′) detected by antibody staining in G2 interphase and mitotic cells in the pupal dorsal thorax tissue. As observed for GFP–Mud (Fig. 1b and Extended data Fig. 1j–m), the endogenous Mud is enriched at TCJ where it co-localizes with Gli in G2 interphase and mitotic cells. Yellow arrows indicate Mud on the spindle poles. n = 37 cells (n, n′′) and n = 21 cells (o, o′′). Scale bars, 1 μm (a, c, d–g, i, j, k, l, m, n, o), 3 min (h).
Extended Data Figure 2 GFP–Mud localizes at TCJ from G2 interphase to mitosis.
a, Scheme depicting the accumulation of the Drosophila FUCCI reporters during the cell cycle. ECFP–E2F1 accumulates during G1 phase, G2 phase and mitosis, whereas mRFP1–CycB accumulates during S phase, G2 phase and mitosis55. b, Localization of GFP–Mud (green left column and white in the second column panels), mRFP1–CycB (red in the left column and white in the third column panels) and ECFP–E2F1 (blue in the left column and white in the right column panels) in epithelial cells of the pupal notum tissue. Confocal sections at the level of septate junctions are shown. Cells in G1 (n = 21), S (n = 6), G2 (n = 35) phases and mitosis (n = 6) are indicated in the left panels. During both G1 and S phase (upper two rows of panels), GFP–Mud is weakly localized at the nuclear envelope membrane, weakly localized at the cortex and at the apically localized centrioles (not shown). During G2 phase GFP–Mud becomes prominently localized at the TCJ (one cell in the first row of panels and two cells in the third row of panels). Arrows indicate examples of TCJ GFP–Mud accumulation. During mitosis GFP–Mud remains localized at the TCJ and accumulates on the spindle and the spindle pole (bottom row panels). Similar results were obtained on fixed tissue for which the cell cycle phases were determined using the PCNA S-phase marker and the nucleus size to distinguish cells in G1 or G2 interphases (not shown). c, GFP–Mud (green arrows) and ChFP–Mud (red arrows) in adjacent tissue patches in G2 (n = 31) and mitotic (n = 8) cells. The FLP/FRT system was used to generate adjacent groups of cells labelled with either GFP–Mud or ChFP–Mud. By analysing the distribution of GFP–Mud in dividing cells adjacent to ChFP–Mud interphasic cells, we found that GFP–Mud was localized at the TCJs of the dividing cell from G2 through mitosis. Scale bars, 1 μm.
Extended Data Figure 3 Regulation of Dlg, Gli and Mud localization in epithelial tissue.
a, b, Localizations of Gli (white in a and green in a′, n = 2 clones) and Dlg (white in b and green in b′, n = 3 clones) in fixed notum tissues harbouring mud clones (identified by loss of mRFP–nls, red in a′–b′). The loss of Mud function does not modify the Gli and Dlg localizations at septate junctions. c, Localization of Gli–YFP (white in c and green in c′) in live notum tissue harbouring a clone of dlg (identified by the loss of mRFP–nls, red in c′, n = 13 clones). The loss of Dlg function results in a loss of Gli localization at TCJs. d, Localization of Dlg–GFP (white in d and green in d′) in live epithelial dorsal thorax tissue harbouring a Gli clone (identified by expression of PH–ChFP, red in d′, n = 5 clones). The loss of Gli function does not affect the distribution of Dlg–GFP at the septate junctions. Scale bars, 5 μm.
Extended Data Figure 4 Astral microtubules contact Mud at the TCJ.
a, a′, Time-lapse images of ChFP–Mud (green in a and top panels of a′, white in bottom panel of a′) and of Jupiter–GFP (red in a and top panels of a′, white in middle panel of a′) in dividing cells (n = 11) in the Drosophila pupal notum tissue. The panels in a′ are magnifications of the boxed region in a. Yellow arrow indicates an astral microtubule that contacts ChFP–Mud at the cortex and shortens concomitant to the spindle pole movement towards the TCJ and spindle rotation. The dashed line corresponds to the initial spindle orientation and the solid lines correspond to its orientation at the final time point (see Supplementary Video 2). Similar results were obtained in cells expressing GFP–Mud and αTub–RFP to label the microtubules (data not shown). b, Schematic of the laser-ablation assay used to estimate the origin and magnitude of forces on astral microtubules required for spindle orientation in the Drosophila pupal dorsal thorax epithelium. Upon ablation (red lines, top), pulling forces (green arrows, left column) or pushing forces (green arrows, right column) yield recoil away (grey arrow, left column) or towards the ablation site (grey arrow, right column), respectively. Scale bars, 1 μm.
Extended Data Figure 5 A large proportion of mitotic spindles remain planar in the absence of Mud, Dlg and Dynein function.
Loss of Mud activity is known to induce defects in mitotic spindle orientation relative to the apical–basal axis (AB) of the cell31,34,56. Nonetheless, in mud, dlg, dynein (glDN) mutant cells around 50% of the epithelial cell divide with an AB angle (αAB) in the range of the wild-type tissue (a–e). Since a large proportion of the spindles remain within the plane of the tissue, all analyses reported in the manuscript were performed on cell divisions that occurred within the plane of the tissue. Furthermore, in a central region of the tissue (box in f and f′), 88% of the divisions in mud tissue occur with an αAB in the range of the wild-type tissue (g). This region was analysed to compare TCJ bipolarity and cell-shape-based predictions of division orientation in wild-type and mud tissue (Fig. 3h). a, AB views of a dividing epithelial cell in wild-type (left panel, out of 257 cells quantified in b) or mud (right panels, out of 176 cells quantified in b) tissue. The spindle is labelled using Jupiter–GFP (green) and the centrosomes using Sas-4–RFP (red). αAB varies from 0° (spindle parallel to the plane of the tissue) to 90° (spindle perpendicular to the plane of the tissue). b, Quantification of αAB in wild-type, mud and in mud tissue expressing GFP–Mud (mud, GFP–Mud). In wild-type tissue, αAB varies between 0 and 22° (blue dashed line). In mud tissue, 56% of cells divide with a αAB angle lower than 22° (dashed red lines). The expression of GFP–Mud in mud tissue rescues the spindle AB orientation phenotype caused by Mud loss of function. Numbers of cells (n) for each genotype are indicated. The distribution of angles in mud tissue is significantly different from wild type (P < 1 × 10−4), and is restored in mud, GFP–mud (P < 1 × 10−4). P values, Kolmogorov–Smirnov test. c, Quantification of αAB in wild-type, Gαi and pins. The loss of either Gαi or Pins function does not affect the orientation of the spindle relative to the plane of tissue (P > 0.3) in agreement with our findings that Mud localization at TCJs is independent of Pins and Gαi. The analysis in pins tissue confirmed previously published findings46. Number of cells (n) are indicated. P values, Kolmogorov–Smirnov test. d, e, Quantification of αAB in wild-type, Gli and dlg tissues at 25 °C (d) and in wild-type and glDN tissues at 29 °C (e). Gli loss of function does not affect αAB orientation, whereas 46% of the dlg cells (P < 1 × 10−4) and 59% of the glDN cells (P < 1 × 10−4) divide with αAB lower than 22° and 24°, respectively. Numbers of cells (n) are indicated. P values, Kolmogorov–Smirnov test. f, f′, Identification of a region of the notum where AB orientation of the spindle is not affected in mud mutant tissue. Defects in AB orientation of the mitotic spindle result in size asymmetry of the two daughter cells57. Therefore daughter cell size was initially used as a proxy for the magnitude of spindle misorientation along the AB axis in mud tissue. The maps of daughter cell size asymmetry in wild-type (f) and mud (f′) tissues (green, no size asymmetry; purple, strong size asymmetry) revealed that a region (highlighted by the black box, f, f′) in the mud notum tissue exhibits almost no defects in daughter cell size asymmetry. Accordingly the quantification of spindle AB orientation within the region in wild-type and mud tissue revealed that 88% of the cells of the region divide within the range of the wild-type cells (see g). Anterior is to the right and the dashed back line indicates the midline. Colour coding: purple, daughter cells with strong size asymmetry; green, daughter cells with normal size symmetry; cyan, cells for which no division was detected; grey, cells which left the field of view and were not analysed; yellow, macrocheatae; white, sensory organ precursors (SOPs). g, Quantification of αAB in wild-type and mud tissue in the boxed regions in f and f′ was performed as in b–e. Numbers of cells (n) for each genotype are indicated. Scale bars, 1 μm (a), 100 μm (f, f′).
Extended Data Figure 6 Spindle orientation modelling.
a, Mitotic cell in the Drosophila pupal notum labelled with Jupiter–GFP to label microtubules (n = 23 cells). White arrows indicate astral microtubules. Yellow arrowheads indicate spindle poles. Scale bar, 1 μm. b, Representation of the different parameters that were varied for the predictions based on the GFP–Mud cortical intensity and shape model to estimate their contribution. L, length of the mitotic spindle; N, number of astral microtubules;  , the angle covered by the astral microtubules; and
, the angle covered by the astral microtubules; and  , the GFP–Mud intensity scaling factor. See also Supplementary Table 1. c–f, Cumulative plots of the differences between the theoretical spindle orientation (
, the GFP–Mud intensity scaling factor. See also Supplementary Table 1. c–f, Cumulative plots of the differences between the theoretical spindle orientation ( ) and the experimental spindle orientation (
) and the experimental spindle orientation ( ) angles in GFP–Mud-expressing cells (same cells as in Fig. 2h) for different spindle lengths (c), microtubule number (d), angular extension of astral microtubules (e) and different scaling factor between the GFP–Mud intensity and mechanical pulling force (f). The GFP–Mud model predictions are mostly independent of spindle length, the number of astral microtubules, the angle covered by the astral microtubules or the scaling factor between GFP–Mud intensity and microtubule pulling force. g, Dependence of model prediction on shape or GFP–Mud effective potential depth (±s.e.m.). The y axis quantitates the difference between the theoretical angle (
) angles in GFP–Mud-expressing cells (same cells as in Fig. 2h) for different spindle lengths (c), microtubule number (d), angular extension of astral microtubules (e) and different scaling factor between the GFP–Mud intensity and mechanical pulling force (f). The GFP–Mud model predictions are mostly independent of spindle length, the number of astral microtubules, the angle covered by the astral microtubules or the scaling factor between GFP–Mud intensity and microtubule pulling force. g, Dependence of model prediction on shape or GFP–Mud effective potential depth (±s.e.m.). The y axis quantitates the difference between the theoretical angle ( ) and experimental angle (
) and experimental angle ( ) (1, aligned; −1, perpendicular). A larger potential depth corresponds to more deformed cells for the shape model, and to a sharp and anisotropic GFP–Mud distribution for the cortical model. Model predictions improve with potential depth, suggesting the model can capture the effect of GFP–Mud distributions in a dose-dependent manner. n = 140 cells. h, Definitions of the angles used in the analytical calculation of the contribution of different harmonics to the potential
) (1, aligned; −1, perpendicular). A larger potential depth corresponds to more deformed cells for the shape model, and to a sharp and anisotropic GFP–Mud distribution for the cortical model. Model predictions improve with potential depth, suggesting the model can capture the effect of GFP–Mud distributions in a dose-dependent manner. n = 140 cells. h, Definitions of the angles used in the analytical calculation of the contribution of different harmonics to the potential  . The spindle (heavy black line) makes an angle
. The spindle (heavy black line) makes an angle  with the positive x axis. An astral microtubule (thin black line indicated by the black arrow) projects to the cortex (circle) at an angle
with the positive x axis. An astral microtubule (thin black line indicated by the black arrow) projects to the cortex (circle) at an angle  with respect to the spindle. The same microtubule contacts the cortex an angle
with respect to the spindle. The same microtubule contacts the cortex an angle  above the positive x axis. i, Normalized magnitudes
above the positive x axis. i, Normalized magnitudes  of the Fourier coefficients of the kernel
of the Fourier coefficients of the kernel  for n even. The magnitudes
for n even. The magnitudes  drop off substantially with increasing n, indicating that for many purposes it should be sufficient to approximate the function
drop off substantially with increasing n, indicating that for many purposes it should be sufficient to approximate the function  by its lowest,
by its lowest,  mode. To calculate numerical values for the Fourier coefficients, we took the average of the normalized spindle length
mode. To calculate numerical values for the Fourier coefficients, we took the average of the normalized spindle length  or the n = 140 cells analysed in this paper, obtaining
or the n = 140 cells analysed in this paper, obtaining  ; because it is difficult to precisely estimate
; because it is difficult to precisely estimate  from the available data, coefficients are shown for
from the available data, coefficients are shown for  and
and  in agreement with the astral microtubule distribution observed in a. j, Schematic illustrating the difference between cell shape and cell TCJ bipolarity measurements. An elongated cell and a rounded cell are overlaid (left panels) and shown side-by-side (middle and right panels). In this example, although the two cells have distinct shapes, they have the same TCJ bipolarity. The upper panels illustrate the measurement of cell shape, which uses all the pixels making up the cell (blue bars). The lower panels illustrate the measurement of TCJ bipolarity (red bars), which is solely based on the angular distribution of the TCJs (red dots), only using the unit vectors
in agreement with the astral microtubule distribution observed in a. j, Schematic illustrating the difference between cell shape and cell TCJ bipolarity measurements. An elongated cell and a rounded cell are overlaid (left panels) and shown side-by-side (middle and right panels). In this example, although the two cells have distinct shapes, they have the same TCJ bipolarity. The upper panels illustrate the measurement of cell shape, which uses all the pixels making up the cell (blue bars). The lower panels illustrate the measurement of TCJ bipolarity (red bars), which is solely based on the angular distribution of the TCJs (red dots), only using the unit vectors  pointing from the cell centre (black dot) to each cell TCJ. The TCJ bipolarity therefore characterizes TCJ distribution independently of cell shape, and a correlation observed between the two quantities is not due to a shape bias in the TCJ bipolarity measurement.
pointing from the cell centre (black dot) to each cell TCJ. The TCJ bipolarity therefore characterizes TCJ distribution independently of cell shape, and a correlation observed between the two quantities is not due to a shape bias in the TCJ bipolarity measurement.
Extended Data Figure 7 Pins does not contribute to Mud-dependent epithelial cell division orientation.
a, Rose plots of the difference between the theoretically predicted ( ) and the experimental division (
) and the experimental division ( ) orientation of the mitotic spindle in pins tissue (orange, left rose plot) and wild-type tissue (green, right) based on the GFP–Mud intensity. To facilitate the comparison between the left and the right rose plots, the data are duplicated relative to 0° line (light orange and light green). Number of cells (n) analysed is indicated. P values, Kolmogorov–Smirnov test. b, Quantifications of the co-localization of GFP–Mud with Gli in pins in metaphase cells (mean ± s.e.m.). Number of cells (n) analysed is indicated. ns, not significant (Student’s t-test).
) orientation of the mitotic spindle in pins tissue (orange, left rose plot) and wild-type tissue (green, right) based on the GFP–Mud intensity. To facilitate the comparison between the left and the right rose plots, the data are duplicated relative to 0° line (light orange and light green). Number of cells (n) analysed is indicated. P values, Kolmogorov–Smirnov test. b, Quantifications of the co-localization of GFP–Mud with Gli in pins in metaphase cells (mean ± s.e.m.). Number of cells (n) analysed is indicated. ns, not significant (Student’s t-test).
Extended Data Figure 8 Structure–function analyses of the Mud protein in epithelial cells.
a, Diagram of the domains of the Mud protein: putative actin binding calponin homology domain (CH, amino acids 1–246, blue), coiled-coil domain (CC, amino acids 246–1,868, grey), conserved Numa/Lin-5/Mud domain (NLM, amino acids 1,968–1,998, red), putative transmembrane domain (TM, amino acids 2,456–2,499, yellow), 9× repeat domain (amino acids 1,137–1,515), microtubule-binding domain (MT, amino acids 1,850–2,039) and Pins binding domain (amino acids 1,928–1,982)58,59,60. GFP- or ChFP-tagged deletion constructs and the MudΔCH constructs were generated by BAC recombineering (see Methods for details). The MudΔC allele was generated at the mud locus using a CRISPR/Cas9 approach (see Methods for details). For each mutant allele, its localization at the TJCs and its localization at the spindle pole are indicated. b, Localization of the GFP–Mud, MudΔCH, GFP–MudΔCC, GFP–MudΔPins, GFP–MudΔTM and in G2 interphase and mitotic mud epithelial cells. GFP–Mud, GFP–MudΔCC, GFP–MudΔPins, GFP–MudΔTM proteins were imaged in living tissue, whereas MudΔCH was localized on fixed tissue using Mud antibodies. GFP–Mud (n = 56), MudΔCH (n = 33), GFP–MudΔCC (n = 165), GFP–MudΔPins (n = 42) and GFP–MudΔTM (n = 67) interphase cells. GFP–Mud (n = 15), MudΔCH (n = 4), GFP–MudΔCC (n = 67), GFP–MudΔPins (n = 18) and GFP–MudΔTM (n = 11) mitotic cells. c, Localization of the MudΔC protein (white in the left panels, green in the right panels), Gli (white in the panels in the middle and red in panels at the right) and Cora (magenta in the right panels) in fixed G2 interphase (n = 71) and mitotic (n = 6) cells. The MudΔC protein is not enriched at TJCs and its localization at the spindle pole is strongly reduced. d, Rose plots of the difference between the theoretically predicted ( ) and experimental (
) and experimental ( ) spindle orientation angles in wild-type (left rose plot, green) and mud (right rose plot, orange) tissues based on the distribution of GFP–MudΔCC. The right rose plot is identical to the one shown in Fig. 2l. To facilitate the comparison between the left and the right rose plots, the data are duplicated relative to 0° line (light green and light orange). Number of cells (n) analysed is indicated. P values, Kolmogorov–Smirnov test. Scale bars, 1 μm.
) spindle orientation angles in wild-type (left rose plot, green) and mud (right rose plot, orange) tissues based on the distribution of GFP–MudΔCC. The right rose plot is identical to the one shown in Fig. 2l. To facilitate the comparison between the left and the right rose plots, the data are duplicated relative to 0° line (light green and light orange). Number of cells (n) analysed is indicated. P values, Kolmogorov–Smirnov test. Scale bars, 1 μm.
Extended Data Figure 9 Predicting cell division based on TCJ distribution.
a, a′′, Rose plots of the magnitude of the difference between experimental ( ) and predicted division orientations by the average (60–30 min before mitosis) interphase TCJ bipolarity (
) and predicted division orientations by the average (60–30 min before mitosis) interphase TCJ bipolarity ( ) or cell long axis (
) or cell long axis ( ) in cells for the indicated
) in cells for the indicated  intervals. To facilitate the comparison between the left and the right rose plots, the data are duplicated relative to 0° line (light blue and light red). Kolmogorov–Smirnov test (P values), percentage of total cells (n = 29,388). Panels b and b′′ are identical to panel e in Fig. 3. b, b′′, Rose plots of the magnitude of the difference between experimental (
intervals. To facilitate the comparison between the left and the right rose plots, the data are duplicated relative to 0° line (light blue and light red). Kolmogorov–Smirnov test (P values), percentage of total cells (n = 29,388). Panels b and b′′ are identical to panel e in Fig. 3. b, b′′, Rose plots of the magnitude of the difference between experimental ( ) and predicted division orientations by the average (60–30 min before mitosis) interphase TCJ bipolarity (
) and predicted division orientations by the average (60–30 min before mitosis) interphase TCJ bipolarity ( ) or cell long axis (
) or cell long axis ( ) for the indicated
) for the indicated  intervals. To facilitate the comparison between the left and the right rose plots, the data are duplicated relative to 0° line (light blue and light red). Kolmogorov–Smirnov test (P values), percentage of total cells (n = 29,388). Panels c and c′′ are identical to panel f in Fig. 3. c, Plot of the spindle orientation prediction improvements (colour-coded from dark blue to red) based on TCJ bipolarity over those based on cell shape versus the magnitude of their angular difference (
intervals. To facilitate the comparison between the left and the right rose plots, the data are duplicated relative to 0° line (light blue and light red). Kolmogorov–Smirnov test (P values), percentage of total cells (n = 29,388). Panels c and c′′ are identical to panel f in Fig. 3. c, Plot of the spindle orientation prediction improvements (colour-coded from dark blue to red) based on TCJ bipolarity over those based on cell shape versus the magnitude of their angular difference ( ) and the cell shape anisotropy (
) and the cell shape anisotropy ( ). The plot height is the normalized cell number in each domain of the plot (29,883 cells were analysed in total). As
). The plot height is the normalized cell number in each domain of the plot (29,883 cells were analysed in total). As  increases, the TCJ bipolarity predictions improve over cell shape prediction for both rounded (low
increases, the TCJ bipolarity predictions improve over cell shape prediction for both rounded (low  ) and elongated cells (high
) and elongated cells (high  ). Whereas the rounded cells are characterized by an even distribution along the
). Whereas the rounded cells are characterized by an even distribution along the  axis, the elongated cells are mainly characterized by a strongly skewed distribution towards low
axis, the elongated cells are mainly characterized by a strongly skewed distribution towards low  .
.
Extended Data Figure 10 TCJ bipolarity aligns with mechanical stress.
a, b, Images of the scutellum tissue before and after ablation (ablated region in yellow) in early and late pupa characterized by small isotropic stress (a) and high anisotropic stress (b). Tissue stress was estimated by determining the initial recoiled velocity upon circular ablation in the x and y directions53. First and last images of two time-lapse movies out of the 18 quantified in c are shown. Scale bars, 10 μm. c, Plot of the difference between the orientation of TCJ bipolarity (
( ) and principal strain axis (
) and principal strain axis ( ) as a function of normal stress differences (
) as a function of normal stress differences ( , note that
, note that  ) as estimated up to a prefactor by circular laser ablation. Number of ablations (n) analysed is indicated. The same plot is shown in Fig. 4d. d, Plot of the difference between the orientation of TCJ bipolarity (
) as estimated up to a prefactor by circular laser ablation. Number of ablations (n) analysed is indicated. The same plot is shown in Fig. 4d. d, Plot of the difference between the orientation of TCJ bipolarity ( ) and the orientation of strain (
) and the orientation of strain ( ) as a function of the percentage of cell elongation applied to a simulated cell lattice. When cell elongation increases TCJ bipolarity orientation becomes aligned with the direction of cell elongation. Number of simulations (n) analysed is indicated.
) as a function of the percentage of cell elongation applied to a simulated cell lattice. When cell elongation increases TCJ bipolarity orientation becomes aligned with the direction of cell elongation. Number of simulations (n) analysed is indicated.
Supplementary information
Supplementary Information
This file contains Supplementary Tables 1-2, a Supplementary Discussion and additional references. (PDF 549 kb)
GFP–Mud localizes at TCJ from interphase through mitosis
Time-lapse video of GFP–Mud in an epithelial cell in the Drosophila pupal notum tissue (12 hAPF) from late G2 interphase (t=-22 min) to the end of cytokinesis (t=37 min). t equals 0 min is set at anaphase onset. GFP–Mud is enriched at TCJ from interphase and remains associated with the TCJ upon entry in and during mitosis. White arrows point to some of the GFP–Mud punctate structures localized at TCJ (see also Fig. 1a and Extended Data Fig. 1e-g). (MOV 1980 kb)
Dynamic of astral MTs associate with Mud during spindle movement
Time-lapse video of ChFP–Mud (white in the middle panel, green in the left one) and of the MT associated protein Jupiter–GFP (white in the right panel, red in left one) in a mitotic cell of the Drosophila epithelial pupal notum tissue. The green arrow highlights an astral MT that is in contact with TCJ associated cortical ChFP–Mud structures and that shortens concomitant to spindle pole movement towards this TCJ (see also Extended Data Fig. 4a). (MOV 597 kb)
Ablation of the astral MTs in mitotic cells to estimate the forces exerted on the astral MTs
Time-lapse video of Nrg–GFP, a basal-lateral membrane marker, αTub–GFP to visualize the MTs and YFP–Asl to label the centrosomes during the ablation of the astral MTs of a mitotic cell in the Drosophila pupal notum tissue. The red arrowhead points to the astral MTs that were ablated at t=0 sec. After ablation (t=1.53 sec) the centrosome recoils away from the site of ablation and towards the cell cortex (see also Fig. 2a). (MOV 4172 kb)
Potts simulations of cell lattices in which cells are elongated
This video shows simulated tissues in which cells were elongated, 9.6% and 51%, respectively. Simulations were used to analyse TCJ bipolarity orientation relative to the direction of tissue elongation (see also Fig. 4b and Extended Data Fig. 10d). TCJ bipolarity and cell shape are plotted as red and blue bars, respectively. The number of Monte Carlo steps (MCS) is indicated. (MOV 5936 kb)
Source data
Rights and permissions
About this article
Cite this article
Bosveld, F., Markova, O., Guirao, B. et al. Epithelial tricellular junctions act as interphase cell shape sensors to orient mitosis. Nature 530, 495–498 (2016). https://doi.org/10.1038/nature16970
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature16970
This article is cited by
-
Homeotic compartment curvature and tension control spatiotemporal folding dynamics
Nature Communications (2023)
-
Intrinsic cell rheology drives junction maturation
Nature Communications (2022)
-
ASPP2 maintains the integrity of mechanically stressed pseudostratified epithelia during morphogenesis
Nature Communications (2022)
-
Cortical Cyclin A controls spindle orientation during asymmetric cell divisions in Drosophila
Nature Communications (2022)
-
Multiciliated cells use filopodia to probe tissue mechanics during epithelial integration in vivo
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.