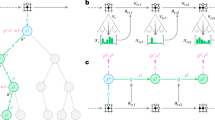
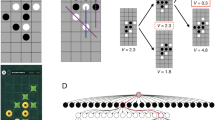
Abstract
The game of Go has long been viewed as the most challenging of classic games for artificial intelligence owing to its enormous search space and the difficulty of evaluating board positions and moves. Here we introduce a new approach to computer Go that uses ‘value networks’ to evaluate board positions and ‘policy networks’ to select moves. These deep neural networks are trained by a novel combination of supervised learning from human expert games, and reinforcement learning from games of self-play. Without any lookahead search, the neural networks play Go at the level of state-of-the-art Monte Carlo tree search programs that simulate thousands of random games of self-play. We also introduce a new search algorithm that combines Monte Carlo simulation with value and policy networks. Using this search algorithm, our program AlphaGo achieved a 99.8% winning rate against other Go programs, and defeated the human European Go champion by 5 games to 0. This is the first time that a computer program has defeated a human professional player in the full-sized game of Go, a feat previously thought to be at least a decade away.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
References
Allis, L. V. Searching for Solutions in Games and Artificial Intelligence. PhD thesis, Univ. Limburg, Maastricht, The Netherlands (1994)
van den Herik, H., Uiterwijk, J. W. & van Rijswijck, J. Games solved: now and in the future. Artif. Intell. 134, 277–311 (2002)
Schaeffer, J. The games computers (and people) play. Advances in Computers 52, 189–266 (2000)
Campbell, M., Hoane, A. & Hsu, F. Deep Blue. Artif. Intell. 134, 57–83 (2002)
Schaeffer, J. et al. A world championship caliber checkers program. Artif. Intell. 53, 273–289 (1992)
Buro, M. From simple features to sophisticated evaluation functions. In 1st International Conference on Computers and Games, 126–145 (1999)
Müller, M. Computer Go. Artif. Intell. 134, 145–179 (2002)
Tesauro, G. & Galperin, G. On-line policy improvement using Monte-Carlo search. In Advances in Neural Information Processing, 1068–1074 (1996)
Sheppard, B. World-championship-caliber Scrabble. Artif. Intell. 134, 241–275 (2002)
Bouzy, B. & Helmstetter, B. Monte-Carlo Go developments. In 10th International Conference on Advances in Computer Games, 159–174 (2003)
Coulom, R. Efficient selectivity and backup operators in Monte-Carlo tree search. In 5th International Conference on Computers and Games, 72–83 (2006)
Kocsis, L. & Szepesvári, C. Bandit based Monte-Carlo planning. In 15th European Conference on Machine Learning, 282–293 (2006)
Coulom, R. Computing Elo ratings of move patterns in the game of Go. ICGA J. 30, 198–208 (2007)
Baudiš, P. & Gailly, J.-L. Pachi: State of the art open source Go program. In Advances in Computer Games, 24–38 (Springer, 2012)
Müller, M., Enzenberger, M., Arneson, B. & Segal, R. Fuego – an open-source framework for board games and Go engine based on Monte-Carlo tree search. IEEE Trans. Comput. Intell. AI in Games 2, 259–270 (2010)
Gelly, S. & Silver, D. Combining online and offline learning in UCT. In 17th International Conference on Machine Learning, 273–280 (2007)
Krizhevsky, A., Sutskever, I. & Hinton, G. ImageNet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems, 1097–1105 (2012)
Lawrence, S., Giles, C. L., Tsoi, A. C. & Back, A. D. Face recognition: a convolutional neural-network approach. IEEE Trans. Neural Netw. 8, 98–113 (1997)
Mnih, V. et al. Human-level control through deep reinforcement learning. Nature 518, 529–533 (2015)
LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015)
Stern, D., Herbrich, R. & Graepel, T. Bayesian pattern ranking for move prediction in the game of Go. In International Conference of Machine Learning, 873–880 (2006)
Sutskever, I. & Nair, V. Mimicking Go experts with convolutional neural networks. In International Conference on Artificial Neural Networks, 101–110 (2008)
Maddison, C. J., Huang, A., Sutskever, I. & Silver, D. Move evaluation in Go using deep convolutional neural networks. 3rd International Conference on Learning Representations (2015)
Clark, C. & Storkey, A. J. Training deep convolutional neural networks to play go. In 32nd International Conference on Machine Learning, 1766–1774 (2015)
Williams, R. J. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Mach. Learn. 8, 229–256 (1992)
Sutton, R., McAllester, D., Singh, S. & Mansour, Y. Policy gradient methods for reinforcement learning with function approximation. In Advances in Neural Information Processing Systems, 1057–1063 (2000)
Sutton, R. & Barto, A. Reinforcement Learning: an Introduction (MIT Press, 1998)
Schraudolph, N. N., Dayan, P. & Sejnowski, T. J. Temporal difference learning of position evaluation in the game of Go. Adv. Neural Inf. Process. Syst. 6, 817–824 (1994)
Enzenberger, M. Evaluation in Go by a neural network using soft segmentation. In 10th Advances in Computer Games Conference, 97–108 (2003). 267
Silver, D., Sutton, R. & Müller, M. Temporal-difference search in computer Go. Mach. Learn. 87, 183–219 (2012)
Levinovitz, A. The mystery of Go, the ancient game that computers still can’t win. Wired Magazine (2014)
Mechner, D. All Systems Go. The Sciences 38, 32–37 (1998)
Mandziuk, J. Computational intelligence in mind games. In Challenges for Computational Intelligence, 407–442 (2007)
Berliner, H. A chronology of computer chess and its literature. Artif. Intell. 10, 201–214 (1978)
Browne, C. et al. A survey of Monte-Carlo tree search methods. IEEE Trans. Comput. Intell. AI in Games 4, 1–43 (2012)
Gelly, S. et al. The grand challenge of computer Go: Monte Carlo tree search and extensions. Commun. ACM 55, 106–113 (2012)
Coulom, R. Whole-history rating: A Bayesian rating system for players of time-varying strength. In International Conference on Computers and Games, 113–124 (2008)
KGS. Rating system math. http://www.gokgs.com/help/rmath.html
Littman, M. L. Markov games as a framework for multi-agent reinforcement learning. In 11th International Conference on Machine Learning, 157–163 (1994)
Knuth, D. E. & Moore, R. W. An analysis of alpha-beta pruning. Artif. Intell. 6, 293–326 (1975)
Sutton, R. Learning to predict by the method of temporal differences. Mach. Learn. 3, 9–44 (1988)
Baxter, J., Tridgell, A. & Weaver, L. Learning to play chess using temporal differences. Mach. Learn. 40, 243–263 (2000)
Veness, J., Silver, D., Blair, A. & Uther, W. Bootstrapping from game tree search. In Advances in Neural Information Processing Systems (2009)
Samuel, A. L. Some studies in machine learning using the game of checkers II - recent progress. IBM J. Res. Develop. 11, 601–617 (1967)
Schaeffer, J., Hlynka, M. & Jussila, V. Temporal difference learning applied to a high-performance game-playing program. In 17th International Joint Conference on Artificial Intelligence, 529–534 (2001)
Tesauro, G. TD-gammon, a self-teaching backgammon program, achieves master-level play. Neural Comput. 6, 215–219 (1994)
Dahl, F. Honte, a Go-playing program using neural nets. In Machines that learn to play games, 205–223 (Nova Science, 1999)
Rosin, C. D. Multi-armed bandits with episode context. Ann. Math. Artif. Intell. 61, 203–230 (2011)
Lanctot, M., Winands, M. H. M., Pepels, T. & Sturtevant, N. R. Monte Carlo tree search with heuristic evaluations using implicit minimax backups. In IEEE Conference on Computational Intelligence and Games, 1–8 (2014)
Gelly, S., Wang, Y., Munos, R. & Teytaud, O. Modification of UCT with patterns in Monte-Carlo Go. Tech. Rep. 6062, INRIA (2006)
Silver, D. & Tesauro, G. Monte-Carlo simulation balancing. In 26th International Conference on Machine Learning, 119 (2009)
Huang, S.-C., Coulom, R. & Lin, S.-S. Monte-Carlo simulation balancing in practice. In 7th International Conference on Computers and Games, 81–92 (Springer-Verlag, 2011)
Baier, H. & Drake, P. D. The power of forgetting: improving the last-good-reply policy in Monte Carlo Go. IEEE Trans. Comput. Intell. AI in Games 2, 303–309 (2010)
Huang, S. & Müller, M. Investigating the limits of Monte-Carlo tree search methods in computer Go. In 8th International Conference on Computers and Games, 39–48 (2013)
Segal, R. B. On the scalability of parallel UCT. Computers and Games 6515, 36–47 (2011)
Enzenberger, M. & Müller, M. A lock-free multithreaded Monte-Carlo tree search algorithm. In 12th Advances in Computer Games Conference, 14–20 (2009)
Huang, S.-C., Coulom, R. & Lin, S.-S. Time management for Monte-Carlo tree search applied to the game of Go. In International Conference on Technologies and Applications of Artificial Intelligence, 462–466 (2010)
Gelly, S. & Silver, D. Monte-Carlo tree search and rapid action value estimation in computer Go. Artif. Intell. 175, 1856–1875 (2011)
Baudiš, P. Balancing MCTS by dynamically adjusting the komi value. ICGA J. 34, 131 (2011)
Baier, H. & Winands, M. H. Active opening book application for Monte-Carlo tree search in 19×19 Go. In Benelux Conference on Artificial Intelligence, 3–10 (2011)
Dean, J. et al. Large scale distributed deep networks. In Advances in Neural Information Processing Systems, 1223–1231 (2012)
Go ratings. http://www.goratings.org
Acknowledgements
We thank Fan Hui for agreeing to play against AlphaGo; T. Manning for refereeing the match; R. Munos and T. Schaul for helpful discussions and advice; A. Cain and M. Cant for work on the visuals; P. Dayan, G. Wayne, D. Kumaran, D. Purves, H. van Hasselt, A. Barreto and G. Ostrovski for reviewing the paper; and the rest of the DeepMind team for their support, ideas and encouragement.
Author information
Authors and Affiliations
Contributions
A.H., G.v.d.D., J.S., I.A., M.La., A.G., T.G. and D.S. designed and implemented the search in AlphaGo. C.J.M., A.G., L.S., A.H., I.A., V.P., S.D., D.G., N.K., I.S., K.K. and D.S. designed and trained the neural networks in AlphaGo. J.S., J.N., A.H. and D.S. designed and implemented the evaluation framework for AlphaGo. D.S., M.Le., T.L., T.G., K.K. and D.H. managed and advised on the project. D.S., T.G., A.G. and D.H. wrote the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
Supplementary information
Supplementary Information
This zipped file contains game records for the 5 formal match games played between AlphaGo and Fan Hui. (ZIP 3 kb)
Rights and permissions
About this article
Cite this article
Silver, D., Huang, A., Maddison, C. et al. Mastering the game of Go with deep neural networks and tree search. Nature 529, 484–489 (2016). https://doi.org/10.1038/nature16961
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature16961
This article is cited by
-
Emerging opportunities and challenges for the future of reservoir computing
Nature Communications (2024)
-
Efficient evolution of human antibodies from general protein language models
Nature Biotechnology (2024)
-
Research on time series prediction of multi-process based on deep learning
Scientific Reports (2024)
-
Large language models help computer programs to evolve
Nature (2024)
-
Efficient retrosynthetic planning with MCTS exploration enhanced A* search
Communications Chemistry (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.