Abstract
To understand the complex physics of a system with strong electron–electron interactions, the ideal is to control and monitor its properties while tuning an external electric field applied to the system (the electric-field effect). Indeed, complete electric-field control of many-body states in strongly correlated electron systems is fundamental to the next generation of condensed matter research and devices1,2,3. However, the material must be thin enough to avoid shielding of the electric field in the bulk material. Two-dimensional materials do not experience electrical screening, and their charge-carrier density can be controlled by gating. Octahedral titanium diselenide (1T-TiSe2) is a prototypical two-dimensional material that reveals a charge-density wave (CDW) and superconductivity in its phase diagram4, presenting several similarities with other layered systems such as copper oxides5, iron pnictides6, and crystals of rare-earth elements and actinide atoms7. By studying 1T-TiSe2 single crystals with thicknesses of 10 nanometres or less, encapsulated in two-dimensional layers of hexagonal boron nitride, we achieve unprecedented control over the CDW transition temperature (tuned from 170 kelvin to 40 kelvin), and over the superconductivity transition temperature (tuned from a quantum critical point at 0 kelvin up to 3 kelvin). Electrically driving TiSe2 over different ordered electronic phases allows us to study the details of the phase transitions between many-body states. Observations of periodic oscillations of magnetoresistance induced by the Little–Parks effect show that the appearance of superconductivity is directly correlated with the spatial texturing of the amplitude and phase of the superconductivity order parameter, corresponding to a two-dimensional matrix of superconductivity. We infer that this superconductivity matrix is supported by a matrix of incommensurate CDW states embedded in the commensurate CDW states. Our results show that spatially modulated electronic states are fundamental to the appearance of two-dimensional superconductivity.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Change history
13 January 2016
Two Extended Data citations in the Methods were corrected.
References
Ueno, K. et al. Electric-field-induced superconductivity in an insulator. Nature Mater. 7, 855–858 (2008)
Bollinger, A. T. et al. Superconductor–insulator transition in La2−xSrxCuO4 at the pair quantum resistance. Nature 472, 458–460 (2011)
Yu, Y. et al. Gate-tunable phase transitions in thin flakes of 1T-TaS2 . Nature Nanotechnol. 10, 270–276 (2014)
Wang, Q. H., Kalantar-Zadeh, K., Kis, A., Coleman, J. N. & Strano, M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nature Nanotechnol. 7, 699–712 (2012)
Shen, K. M. & Davis, J. C. S. Cuprate high-Tc superconductors. Mater. Today 11, 14–21 (2008)
Stewart, G. R. Superconductivity in iron compounds. Rev. Mod. Phys. 83, 1589–1652 (2011)
Stewart, G. R. Heavy-fermion systems. Rev. Mod. Phys. 56, 755–787 (1984)
Castro Neto, A. H. & Jones, B. A. Non-Fermi-liquid behavior in U and Ce alloys: criticality, disorder, dissipation, and Griffiths-McCoy singularities. Phys. Rev. B 62, 14975–15011 (2000)
Kotov, V. N., Uchoa, B., Pereira, V. M., Guinea, F. & Castro Neto, A. H. Electron-electron interactions in graphene: current status and perspectives. Rev. Mod. Phys. 84, 1067–1125 (2012)
Fisher, M. E. & Langer, J. S. Resistive anomalies at magnetic critical points. Phys. Rev. Lett. 20, 665–668 (1968)
Castro Neto, A. H. Charge density wave, superconductivity, and anomalous metallic behavior in 2D transition metal dichalcogenides. Phys. Rev. Lett. 86, 4382–4385 (2001)
Minnhagen, P. The two-dimensional Coulomb gas, vortex unbinding, and superfluid-superconducting films. Rev. Mod. Phys. 59, 1001–1066 (1987)
Reyren, N. et al. Superconducting interfaces between insulating oxides. Science 317, 1196–1199 (2007)
Sachdev, S. Quantum Phase Transitions (Cambridge Univ. Press, 1999)
Caviglia, A. D. et al. Electric field control of the LaAlO3/SrTiO3 interface ground state. Nature 456, 624–627 (2008)
Parendo, K. A. et al. Electrostatic tuning of the superconductor-insulator transition in two dimensions. Phys. Rev. Lett. 94, 197004 (2005)
Aubin, H. et al. Magnetic-field-induced quantum superconductor-insulator transition in Nb0.15Si0.85 . Phys. Rev. B 73, 094521 (2006)
Mason, N. & Kapitulnik, A. Superconductor-insulator transition in a capacitively coupled dissipative environment. Phys. Rev. B 65, 220505 (2002)
Yazdani, A. & Kapitulnik, A. Superconducting-insulating transition in two-dimensional a-MoGe thin films. Phys. Rev. Lett. 74, 3037–3040 (1995)
Harris, A. B. Effect of random defects on the critical behaviour of Ising models. J. Phys. Chem. 7, 1671 (1974)
Tinkham, M. Introduction to Superconductivity (McGraw-Hill, 1975)
McMillan, W. L. Theory of discommensurations and the commensurate-incommensurate charge-density-wave phase transition. Phys. Rev. B 14, 1496–1502 (1976)
McMillan, W. L. Time-dependent Laudau theory of charge-density waves in transition-metal dichalcogenides. Phys. Rev. B 12, 1197–1199 (1975)
Burk, B., Thomson, R. E., Zettl, A. & Clarke, J. Charge-density-wave domains in 1T-TaS2 observed by satellite structure in scanning-tunneling-microscopy images. Phys. Rev. Lett. 66, 3040 (1991)
Kashiwaya, S. & Tanaka, Y. Tunnelling effects on surface bound states in unconventional superconductors. Rep. Prog. Phys. 63, 1641–1724 (2000)
Li, S. Y., Wu, G., Chen, X. H. & Taillefer, L. Single-gap s-wave superconductivity near the charge-density-wave quantum critical point in CuxTiSe2 . Phys. Rev. Lett. 99, 107001 (2007)
Fradkin, E., Kivelson, S. A. & Tranquada, J. M. Theory of intertwined orders in high temperature superconductors. Rev. Mod. Phys. 87, 457 (2015)
Agterberg, D. F. & Tsunetsugu, H. Dislocations and vortices in pair-density-wave superconductors. Nature Phys. 4, 639–642 (2008)
Joe, Y. I. et al. Emergence of charge density wave domain walls above the superconducting dome in 1T-TiSe2 . Nature Phys. 10, 421–425 (2014)
Di Salvo, F. J., Moncton, D. E. & Waszczak, J. V. Electronic properties and superlattice formation in the semimetal TiSe2 . Phys. Rev. B 14, 4321–4328 (1976)
Holy, J. A., Woo, K. C., Klein, M. V. & Brown, F. C. Raman and infrared studies of superlattice formation in TiSe2 . Phys. Rev. B 16, 3628–3637 (1977)
Novoselov, K. S. et al. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004)
Doganov, R. A. et al. Transport properties of pristine few-layer black phosphorus by van der Waals passivation in an inert atmosphere. Nature Commun. 6, 6647 (2015)
Mayorov, A. S. et al. Micrometer-scale ballistic transport in encapsulated graphene at room temperature. Nano Lett. 11, 2396–2399 (2011)
Pu, J. et al. Highly flexible MoS2 thin-film transistors with ion gel dielectrics. Nano Lett. 12, 4013–4017 (2012)
Gallagher, P. et al. A high-mobility electronic system at an electrolyte-gated oxide surface. Nature Commun. 6, 6437 (2015)
Reyren, N. et al. Superconducting interfaces between insulating oxides. Science 317, 1196–1199 (2007)
Fisher, M. P. A. Quantum phase transitions in disordered two-dimensional superconductors. Phys. Rev. Lett. 65, 923–926 (1990)
Pfleiderer, C., Julian, S. R. & Lonzarich, G. G. Non-Fermi-liquid nature of the normal state of itinerant-electron ferromagnets. Nature 414, 427–430 (2001)
Daghero, D. & Gonnelli, R. S. Probing multiband superconductivity by point-contact spectroscopy. Supercond. Sci. Technol 23, 043001 (2010)
Acknowledgements
We thank L. Q. Chu, T. H. Ren, J. Y. Tan, J. Wu and H. Schmidt for experimental assistance, and S. Natarajan for assistance in preparing the manuscript. A.H.C.N. acknowledges many discussions with A. K. Geim and a private communication with P. Abbamonte. K.P.L. acknowledges a MOE Tier 1 grant, “2-D crystals as a platform for optoelectronics (R-143-000-556-112)”. G.E. acknowledges a National Research Foundation (NRF) Research Fellowship (NRF-NRFF2011-02). B.Ö. acknowledges support by the NRF, Prime Minister’s Office, Singapore, under its Competitive Research Programme (CRP award number NRF-CRP9-2011-3), and the SMF-NUS Research Horizons Award 2009-Phase II. A.H.C.N acknowledges the CRP award, “Novel 2D materials with tailored properties: beyond graphene” (NRF-CRP6-2010-05). All authors acknowledge the NRF, Prime Minister’s Office, Singapore, under its Medium-Sized Centre Programme.
Author information
Authors and Affiliations
Contributions
L.J.L. performed the growth and characterization of the single crystal, L.J.L. and E.C.T.O’F. performed device fabrication and carried out the measurement, L.J.L., E.C.T.O’F., K.P.L., B.Ö. and A.H.C.N. analysed the data and wrote the manuscript. All authors commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
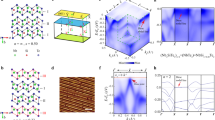
Extended Data Figure 1 Characterization of the high quality of single-crystal TiSe2.
a, X-ray diffraction of both single-crystal and powder TiSe2 sample. The inset shows the as-grown TiSe2 single crystal. b, Raman spectroscopy pattern at both high temperature and low temperature. The two main phonon modes, Eg and A1g, are distinct, whereas only below TCDW are the peaks corresponding to CDW phonon mode detectable. The inset displays the unit cell of the TiSe2 lattice and the main phonon mode vectors.
Extended Data Figure 2 The Hall bar device and its characterization by Hall effect measurement.
a, Optical microscope picture. b, Atomic force microscope picture of the Hall bar device. c, Temperature dependence of the charge-carrier density measured by the Hall effect at different top gate voltages, VTG. Scale bar, 5 μm.
Extended Data Figure 3 Characterization of the K–T transition.
a, The current–voltage power-law fit for n = 5.9 × 1014 cm−2 at different temperatures is consistent with the behaviour of the 2D K–T transition. b, Temperature-dependent magnetoresistance of the superconducting transition at different fixed perpendicular magnetic fields for n = 2.67 × 1014 cm−2. c, The magnetoresistance data in b collapses into two sets of lines by so-called finite size scaling.
Extended Data Figure 4 The R versus T power-law fit indicates the existence of strong quantum fluctuation.
a, Temperature dependence of the sheet resistance for different doping levels. b, The data shown in a is plotted on a log–log scale.
Extended Data Figure 5 The magnetoresistance oscillation for charge-carrier densities of 1.3 × 1014 and 2.7 × 1014 cm−2.
a, c, Perpendicular magnetic-field-dependent magnetoresistance measured at different temperatures. b, d, Plots of dRS/dB against B and T for n =1.3 × 1014 cm−2 and n = 2.7 × 1014 cm−2, respectively.
Extended Data Figure 6 The conductance measured for a charge-carrier density of 2.1 × 1014 cm−2.
a, Magnetic field dependence at 0.1 K. b, Temperature dependence at zero magnetic field. a.u., arbitrary units.
Rights and permissions
About this article
Cite this article
Li, L., O’Farrell, E., Loh, K. et al. Controlling many-body states by the electric-field effect in a two-dimensional material. Nature 529, 185–189 (2016). https://doi.org/10.1038/nature16175
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature16175
This article is cited by
-
Persistence of charge density wave against variation of band structures in VxTi1−xSe2(x = 0−0.1)
Nano Research (2024)
-
Tunable sliding ferroelectricity and magnetoelectric coupling in two-dimensional multiferroic MnSe materials
npj Computational Materials (2023)
-
Superconductivity induced by gate-driven hydrogen intercalation in the charge-density-wave compound 1T-TiSe2
Communications Physics (2023)
-
Superconducting dome by tuning through a van Hove singularity in a two-dimensional metal
npj 2D Materials and Applications (2023)
-
Intrinsic spin Hall resonance in Bi-based Janus monolayers
Nano Research (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.