Abstract
The whole frame of interconnections in complex networks hinges on a specific set of structural nodes, much smaller than the total size, which, if activated, would cause the spread of information to the whole network1, or, if immunized, would prevent the diffusion of a large scale epidemic2,3. Localizing this optimal, that is, minimal, set of structural nodes, called influencers, is one of the most important problems in network science4,5. Despite the vast use of heuristic strategies to identify influential spreaders6,7,8,9,10,11,12,13,14, the problem remains unsolved. Here we map the problem onto optimal percolation in random networks to identify the minimal set of influencers, which arises by minimizing the energy of a many-body system, where the form of the interactions is fixed by the non-backtracking matrix15 of the network. Big data analyses reveal that the set of optimal influencers is much smaller than the one predicted by previous heuristic centralities. Remarkably, a large number of previously neglected weakly connected nodes emerges among the optimal influencers. These are topologically tagged as low-degree nodes surrounded by hierarchical coronas of hubs, and are uncovered only through the optimal collective interplay of all the influencers in the network. The present theoretical framework may hold a larger degree of universality, being applicable to other hard optimization problems exhibiting a continuous transition from a known phase16.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Domingos, P. & Richardson, M. Mining knowledge-sharing sites for viral marketing. In Proc. 8th ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, 61–70 (ACM, 2002); http://dx.doi.org/10.1145/775047.775057
Pastor-Satorras, R. & Vespignani, A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 86, 3200–3203 (2001)
Newman, M. E. J. Spread of epidemic disease on networks. Phys. Rev. E 66, 016128 (2002)
Kempe, D., Kleinberg, J. & Tardos, E. Maximizing the spread of influence through a social network. In Proc. 9th ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, 137–143 (ACM, 2003); http://dx.doi.org/10.1145/956750.956769
Newman, M. E. J. Networks: An Introduction (Oxford Univ. Press, 2010)
Freeman, L. C. Centrality in social networks: conceptual clarification. Soc. Networks 1, 215–239 (1978)
Brin, S. & Page, L. The anatomy of a large-scale hypertextual web search engine. Comput. Networks ISDN Systems 30, 107–117 (1998)
Kleinberg, J. Authoritative sources in a hyperlinked environment. In Proc. 9th ACM-SIAM Symp. on Discrete Algorithms (1998); J. Assoc. Comput. Machinery 46, 604–632 (1999)
Albert, R., Jeong, H. & Barabási, A.-L. Error and attack tolerance of complex networks. Nature 406, 378–382 (2000)
Cohen, R., Erez, K., ben-Avraham, D. & Havlin, S. Breakdown of the Internet under intentional attack. Phys. Rev. Lett. 86, 3682–3685 (2001)
Chen, Y., Paul, G., Havlin, S., Liljeros, F. & Stanley, H. E. Finding a better immunization strategy. Phys. Rev. Lett. 101, 058701 (2008)
Kitsak, M. et al. Identification of influential spreaders in complex networks. Nature Phys. 6, 888–893 (2010)
Altarelli, F., Braunstein, A., Dall’Asta, L. & Zecchina, R. Optimizing spread dynamics on graphs by message passing. J. Stat. Mech. P09011 (2013)
Altarelli, F., Braunstein, A., Dall’Asta, L., Wakeling, J. R. & Zecchina, R. Containing epidemic outbreaks by message-passing techniques. Phys. Rev. X 4, 021024 (2014)
Hashimoto, K. Zeta functions of finite graphs and representations of p-adic groups. Adv. Stud. Pure Math. 15, 211–280 (1989)
Coja-Oghlan, A., Mossel, E. & Vilenchik, D. A spectral approach to analyzing belief propagation for 3-coloring. Combin. Probab. Comput. 18, 881–912 (2009)
Granovetter, M. Threshold models of collective behavior. Am. J. Sociol. 83, 1420–1443 (1978)
Watts, D. J. A simple model of global cascades on random networks. Proc. Natl Acad. Sci. USA 99, 5766–5771 (2002)
Pei, S., Muchnik, L., Andrade, J. S., Jr, Zheng, Z. & Makse, H. A. Searching for superspreaders of information in real-world social media. Sci. Rep. 4, 5547 (2014)
Pei, S. & Makse, H. A. Spreading dynamics in complex networks. J. Stat. Mech. P12002 (2013)
Bollobás, B. & Riordan, O. Percolation (Cambridge Univ. Press, 2006)
Bianconi, G. & Dorogovtsev, S. N. Multiple percolation transitions in a configuration model of network of networks. Phys. Rev. E 89, 062814 (2014)
Karrer, B., Newman, M. E. J. & Zdeborová, L. Percolation on sparse networks. Phys. Rev. Lett. 113, 208–702 (2014)
Angel, O., Friedman, J. & Hoory, S. The non-backtracking spectrum of the universal cover of a graph. Trans. Am. Math. Soc. 367, 4287–4318 (2015)
Krzakala, F. et al. Spectral redemption in clustering sparse networks. Proc. Natl Acad. Sci. USA 110, 20935–20940 (2013)
Newman, M. E. J. Spectral methods for community detection and graph partitioning. Phys. Rev. E 88, 042822 (2013)
Radicchi, F. Predicting percolation thresholds in networks. Phys. Rev. E 91, 010801(R) (2015)
Mézard, M. & Parisi, G. The cavity method at zero temperature. J. Stat. Phys. 111, 1–34 (2003)
Boettcher, S. & Percus, A. G. Optimization with extremal dynamics. Phys. Rev. Lett. 86, 5211–5214 (2001)
Granovetter, M. The strength of weak ties. Am. J. Sociol. 78, 1360–1380 (1973)
Acknowledgements
This work was funded by NIH-NIGMS 1R21GM107641 and NSF-PoLS PHY-1305476. Additional support was provided by Army Research Laboratory Cooperative Agreement Number W911NF-09-2-0053 (the ARL Network Science CTA). We thank L. Bo, S. Havlin and R. Mari for discussions and Grandata for providing the data on mobile phone calls.
Author information
Authors and Affiliations
Contributions
Both authors contributed equally to the work presented in this paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
Extended Data Figure 1 High-degree (HD) threshold.
a, HD influence threshold qc as a function of the degree distribution exponent γ of scale-free networks in the ensemble with kmax = mN1/(γ−1) and N → ∞. The curves refer to different values of the minimum degree m: 1 (red), 2 (blue), 3 (black). The fragility of SF networks (small qc) is notable for m = 1 (the case calculated in ref. 10). In this case (m = 1), the network contains many leaves, and reduces to a star at γ = 2, which is trivially destroyed by removing the only single hub, explaining the general fragility in this case. Furthermore, in this same case, the network becomes a collection of dimers with k = 1 when γ → ∞, which is still trivially fragile. This also explains why qc → 0 for γ ≥ 4. Therefore, the fragility in the case m = 1 has its roots in these two limiting trivial cases. Removing the leaves (m = 2) results in a 2-core, which is already more robust. For the 3-core m = 3, qc ≈ 0.4–0.5 provides a quite robust network, and has the expected asymptotic limit to a non-zero qc of a random regular graph with k = 3 as γ → ∞, qc → (k − 2)/(k − 1) = 0.5. Thus, SF networks become robust in these more realistic cases, and the search for other attack strategies becomes even more important. b, HD influence threshold qc as a function of the degree distribution exponent of scale-free networks with minimum degree m = 2 in the ensemble where kmax is fixed and does not scale with N. The curves refer to different values of the cut-off kmax: 102 (red), 103 (green), 105 (blue), 108 (magenta), and kmax = ∞ (black), and show that for a typical kmax degree of 103, for instance in social networks, the network is fairly robust with qc ≈ 0.2 for all γ. The curve with m = 2 and kmax = 103 is replotted in the inset of Fig. 2b.
Extended Data Figure 2 Replica Symmetry (RS) estimation of the maximum eigenvalue.
Main panel, the eigenvalue  , equation (92) in Supplementary Information for the two-body interaction ℓ = 1, obtained by minimizing the energy function
, equation (92) in Supplementary Information for the two-body interaction ℓ = 1, obtained by minimizing the energy function  with the RS cavity method. The curve was computed on an ER graph of N = 10,000 nodes and average degree 〈k〉 = 3.5 and then averaged over 40 realizations of the network (error bars are s.e.m.). Inset, comparison between the RS cavity method and EO (extremal optimization) for an ER graph of 〈k〉 = 3.5 and N = 128. The curves are averaged over 200 realizations (error bars are s.e.m.).
with the RS cavity method. The curve was computed on an ER graph of N = 10,000 nodes and average degree 〈k〉 = 3.5 and then averaged over 40 realizations of the network (error bars are s.e.m.). Inset, comparison between the RS cavity method and EO (extremal optimization) for an ER graph of 〈k〉 = 3.5 and N = 128. The curves are averaged over 200 realizations (error bars are s.e.m.).
Extended Data Figure 3 EO estimation of the maximum eigenvalue.
Eigenvalue λ(q) obtained by minimizing the energy function  (n) with τEO (τ-extremal optimization), plotted as a function of the fraction of removed nodes q. The panels are for different orders of the interactions. The curves in each panel refer to different sizes of ER networks with average connectivity 〈k〉 = 3.5. Each curve is an average over 200 instances (error bars are s.e.m.). The value qc where λ(qc) = 1 is the threshold for a particular N and many-body interaction.
(n) with τEO (τ-extremal optimization), plotted as a function of the fraction of removed nodes q. The panels are for different orders of the interactions. The curves in each panel refer to different sizes of ER networks with average connectivity 〈k〉 = 3.5. Each curve is an average over 200 instances (error bars are s.e.m.). The value qc where λ(qc) = 1 is the threshold for a particular N and many-body interaction.
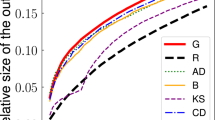
Extended Data Figure 4 Estimation of optimal threshold  with EO.
with EO.
a, Critical threshold qc as a function of the system size N, obtained with EO from Extended Data Fig. 3, of ER networks with 〈k〉 = 3.5 and varying size. The curves refer to different orders of the many-body interactions. The data show a linear behaviour as a function of N−2/3, typical of spin glasses, for each many-body interaction ρ. The extrapolated value  is obtained at the y intercept. b, Thermodynamic critical threshold
is obtained at the y intercept. b, Thermodynamic critical threshold  as a function of the order of the interactions ρ from a. The data scale linearly with 1/ρ. From the y intercept of the linear fit we obtain the thermodynamic limit of the infinite-body optimal value
as a function of the order of the interactions ρ from a. The data scale linearly with 1/ρ. From the y intercept of the linear fit we obtain the thermodynamic limit of the infinite-body optimal value  .
.
Extended Data Figure 5 Comparison of the CI algorithm for different radii ℓ of the Ball(ℓ).
We use ℓ = 1, 2, 3, 4, 5, on a ER graph with average degree 〈k〉 = 3.5 and N = 105 (the average is taken over 20 realizations of the network, error bars are s.e.m.). For ℓ = 3 the performance is already practically indistinguishable from ℓ = 4, 5. The stability analysis we developed to minimize qc is strictly valid only when G = 0, since the largest eigenvalue of the modified NB matrix controls the stability of the solution G = 0, and not the stability of the solution G > 0. In the region where G > 0 we use a simple and fast procedure to minimize G explained in Supplementary Information section VA. This explains why there is a small dependence on having a slightly larger G for larger ℓ, when G > 0 in the region q ≈ 0.15.
Extended Data Figure 6 Illustration of the algorithm used to minimize G(q) for q < qc.
Starting from the completely fragmented network at q = qc, the Nqc influencers are reinserted with their original degree and connected to their original neighbours with the following criterion: each node is assigned and index c(i) given by the number of clusters it would join if it were reinserted in the network. For example, the red node has c(red) = 2, while the blue one has c(blue) = 3. The node with the smallest c(i) is reinserted in the network: in this case the red node. Then the c(i)s are recalculated and the new node with the smallest c(i) is found and reinserted. These steps are repeated until all the removed nodes are reinserted in the network.
Extended Data Figure 7 Test of the decimation fraction.
Giant component G as a function of the fraction of removed nodes q using CI, for an ER network of N = 105 nodes and average degree 〈k〉 = 3.5. The profiles of the curves are drawn for different percentages of nodes fixed at each step of the decimation algorithm.
Extended Data Figure 8 Comparison of the performance of CI, BC and EGP in destroying G.
We also include HD, HDA, EC, CC, k-core and PR. We use a scale-free (SF) network with degree exponent γ = 2.5, average degree 〈k〉 = 4.68, and N = 104. We use the same parameters as in ref. 11.
Extended Data Figure 9 Comparison with BP for a network immunization.
a, Fraction of infected nodes f as a function of the fraction of immunized nodes q in the susceptible-infected-removed (SIR) model from the BP solution. We use an ER random graph of N = 200 nodes and average degree 〈k〉 = 3.5. The fraction of initially infected nodes is p = 0.1 and the inverse temperature β = 3.0. The profiles are drawn for different values of the transmission probability w: 0.4 (red curve), 0.5 (green), 0.6 (blue), 0.7 (magenta). Also shown are the results of the fixed density BP algorithm (open circles). b, Chemical potential μ as a function of the immunized nodes q from BP. We use an ER random graph of N = 200 nodes and average degree 〈k〉 = 3.5. The fraction of the initially infected nodes is p = 0.1 and the inverse temperature β = 3.0. The profiles are drawn for different values of the transmission probability w: 0.4 (red curve), 0.5 (green), 0.6 (blue), 0.7 (magenta). Also shown are the results of the fixed density BP algorithm (open circles) for the region where the chemical potential is non-convex. c, Comparison between the giant components obtained with CI, HDA, HD and BP. We use an ER network of N = 103 and 〈k〉 = 3.5. We also show the solution of CI from Fig. 2a for N = 105. We find in order of performance: CI, HDA, BP and HD. (The average is taken over 20 realizations of the network, error bars are s.e.m.) d, Comparison between the giant components obtained with CI, HDA, HD and BPD. We use a SF network with degree exponent γ = 3.0, minimum degree kmin = 2, and N = 104 nodes.
Extended Data Figure 10 Fraction of infected nodes f(q) as a function of the fraction of immunized nodes q in SIR from BP.
We use the following parameters: initial fraction of infected people p = 0.1, and transmission probability w = 0.5. We use an ER network of N = 103 nodes and 〈k〉 = 3.5. We compare CI, HDA and BP. All strategies give similar performance, owing to the large value of the initial infection p, which washes out the optimization performed by any sensible strategy, in agreement with the results shown in figure 12a of ref. 14.
Supplementary information
Supplementary Information
This file contains Supplementary Text and Data and Supplementary References. (PDF 1656 kb)
Rights and permissions
About this article
Cite this article
Morone, F., Makse, H. Influence maximization in complex networks through optimal percolation. Nature 524, 65–68 (2015). https://doi.org/10.1038/nature14604
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature14604
This article is cited by
-
Protein–protein interaction network-based integration of GWAS and functional data for blood pressure regulation analysis
Human Genomics (2024)
-
Robustness and resilience of complex networks
Nature Reviews Physics (2024)
-
Identifying key players in complex networks via network entanglement
Communications Physics (2024)
-
DomiRank Centrality reveals structural fragility of complex networks via node dominance
Nature Communications (2024)
-
An insight into topological, machine and Deep Learning-based approaches for influential node identification in social media networks: a systematic review
Multimedia Systems (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.



 with EO.
with EO.