Abstract
The standard model of particle physics describes the fundamental particles and their interactions via the strong, electromagnetic and weak forces. It provides precise predictions for measurable quantities that can be tested experimentally. The probabilities, or branching fractions, of the strange B meson ( ) and the B0 meson decaying into two oppositely charged muons (μ+ and μ−) are especially interesting because of their sensitivity to theories that extend the standard model. The standard model predicts that the
) and the B0 meson decaying into two oppositely charged muons (μ+ and μ−) are especially interesting because of their sensitivity to theories that extend the standard model. The standard model predicts that the  and
and  decays are very rare, with about four of the former occurring for every billion
decays are very rare, with about four of the former occurring for every billion  mesons produced, and one of the latter occurring for every ten billion B0 mesons1. A difference in the observed branching fractions with respect to the predictions of the standard model would provide a direction in which the standard model should be extended. Before the Large Hadron Collider (LHC) at CERN2 started operating, no evidence for either decay mode had been found. Upper limits on the branching fractions were an order of magnitude above the standard model predictions. The CMS (Compact Muon Solenoid) and LHCb (Large Hadron Collider beauty) collaborations have performed a joint analysis of the data from proton–proton collisions that they collected in 2011 at a centre-of-mass energy of seven teraelectronvolts and in 2012 at eight teraelectronvolts. Here we report the first observation of the
mesons produced, and one of the latter occurring for every ten billion B0 mesons1. A difference in the observed branching fractions with respect to the predictions of the standard model would provide a direction in which the standard model should be extended. Before the Large Hadron Collider (LHC) at CERN2 started operating, no evidence for either decay mode had been found. Upper limits on the branching fractions were an order of magnitude above the standard model predictions. The CMS (Compact Muon Solenoid) and LHCb (Large Hadron Collider beauty) collaborations have performed a joint analysis of the data from proton–proton collisions that they collected in 2011 at a centre-of-mass energy of seven teraelectronvolts and in 2012 at eight teraelectronvolts. Here we report the first observation of the  µ+µ− decay, with a statistical significance exceeding six standard deviations, and the best measurement so far of its branching fraction. Furthermore, we obtained evidence for the
µ+µ− decay, with a statistical significance exceeding six standard deviations, and the best measurement so far of its branching fraction. Furthermore, we obtained evidence for the  µ+µ− decay with a statistical significance of three standard deviations. Both measurements are statistically compatible with standard model predictions and allow stringent constraints to be placed on theories beyond the standard model. The LHC experiments will resume taking data in 2015, recording proton–proton collisions at a centre-of-mass energy of 13 teraelectronvolts, which will approximately double the production rates of
µ+µ− decay with a statistical significance of three standard deviations. Both measurements are statistically compatible with standard model predictions and allow stringent constraints to be placed on theories beyond the standard model. The LHC experiments will resume taking data in 2015, recording proton–proton collisions at a centre-of-mass energy of 13 teraelectronvolts, which will approximately double the production rates of  and B0 mesons and lead to further improvements in the precision of these crucial tests of the standard model.
and B0 mesons and lead to further improvements in the precision of these crucial tests of the standard model.
Similar content being viewed by others
Main
Experimental particle physicists have been testing the predictions of the standard model of particle physics (SM) with increasing precision since the 1970s. Theoretical developments have kept pace by improving the accuracy of the SM predictions as the experimental results gained in precision. In the course of the past few decades, the SM has passed critical tests derived from experiment, but it does not address some profound questions about the nature of the Universe. For example, the existence of dark matter, which has been confirmed by cosmological data3, is not accommodated by the SM. It also fails to explain the origin of the asymmetry between matter and antimatter, which after the Big Bang led to the survival of the tiny amount of matter currently present in the Universe3,4. Many theories have been proposed to modify the SM to provide solutions to these open questions.
The  and B0 mesons are unstable particles that decay via the weak interaction. The measurement of the branching fractions of the very rare decays of these mesons into a dimuon (µ+µ−) final state is especially interesting.
and B0 mesons are unstable particles that decay via the weak interaction. The measurement of the branching fractions of the very rare decays of these mesons into a dimuon (µ+µ−) final state is especially interesting.
At the elementary level, the weak force is composed of a ‘charged current’ and a ‘neutral current’ mediated by the W± and Z0 bosons, respectively. An example of the charged current is the decay of the π+ meson, which consists of an up (u) quark of electrical charge +2/3 of the charge of the proton and a down (d) antiquark of charge +1/3. A pictorial representation of this process, known as a Feynman diagram, is shown in Fig. 1a. The u and d quarks are ‘first generation’ or lowest mass quarks. Whenever a decay mode is specified in this Letter, the charge conjugate mode is implied.
 →μ+μ− decay.
→μ+μ− decay.a, π+ meson decay through the charged-current process; b, B+ meson decay through the charged-current process; c, a  decay through the direct flavour changing neutral current process, which is forbidden in the SM, as indicated by a large red ‘X’; d, e, higher-order flavour changing neutral current processes for the
decay through the direct flavour changing neutral current process, which is forbidden in the SM, as indicated by a large red ‘X’; d, e, higher-order flavour changing neutral current processes for the  decay allowed in the SM; and f and g, examples of processes for the same decay in theories extending the SM, where new particles, denoted X0 and X+, can alter the decay rate.
decay allowed in the SM; and f and g, examples of processes for the same decay in theories extending the SM, where new particles, denoted X0 and X+, can alter the decay rate.
The B+ meson is similar to the π+, except that the light d antiquark is replaced by the heavy ‘third generation’ (highest mass quarks) beauty (b) antiquark, which has a charge of +1/3 and a mass of ∼5 GeV/c2 (about five times the mass of a proton). The decay B+→ µ+ν, represented in Fig. 1b, is allowed but highly suppressed because of angular momentum considerations (helicity suppression) and because it involves transitions between quarks of different generations (CKM suppression), specifically the third and first generations of quarks. All b hadrons, including the B+,  and B0 mesons, decay predominantly via the transition of the b antiquark to a ‘second generation’ (intermediate mass quarks) charm (c) antiquark, which is less CKM suppressed, into final states with charmed hadrons. Many allowed decay modes, which typically involve charmed hadrons and other particles, have angular momentum configurations that are not helicity suppressed.
and B0 mesons, decay predominantly via the transition of the b antiquark to a ‘second generation’ (intermediate mass quarks) charm (c) antiquark, which is less CKM suppressed, into final states with charmed hadrons. Many allowed decay modes, which typically involve charmed hadrons and other particles, have angular momentum configurations that are not helicity suppressed.
The neutral  meson is similar to the B+ except that the u quark is replaced by a second generation strange (s) quark of charge −1/3. The decay of the
meson is similar to the B+ except that the u quark is replaced by a second generation strange (s) quark of charge −1/3. The decay of the  meson to two muons, shown in Fig. 1c, is forbidden at the elementary level because the Z0 cannot couple directly to quarks of different flavours, that is, there are no direct ‘flavour changing neutral currents’. However, it is possible to respect this rule and still have this decay occur through ‘higher order’ transitions such as those shown in Fig. 1d and e. These are highly suppressed because each additional interaction vertex reduces their probability of occurring significantly. They are also helicity and CKM suppressed. Consequently, the branching fraction for the
meson to two muons, shown in Fig. 1c, is forbidden at the elementary level because the Z0 cannot couple directly to quarks of different flavours, that is, there are no direct ‘flavour changing neutral currents’. However, it is possible to respect this rule and still have this decay occur through ‘higher order’ transitions such as those shown in Fig. 1d and e. These are highly suppressed because each additional interaction vertex reduces their probability of occurring significantly. They are also helicity and CKM suppressed. Consequently, the branching fraction for the  decay is expected to be very small compared to the dominant b antiquark to c antiquark transitions. The corresponding decay of the B0 meson, where a d quark replaces the s quark, is even more CKM suppressed because it requires a jump across two quark generations rather than just one.
decay is expected to be very small compared to the dominant b antiquark to c antiquark transitions. The corresponding decay of the B0 meson, where a d quark replaces the s quark, is even more CKM suppressed because it requires a jump across two quark generations rather than just one.
The branching fractions,  , of these two decays, accounting for higher-order electromagnetic and strong interaction effects, and using lattice quantum chromodynamics to compute the
, of these two decays, accounting for higher-order electromagnetic and strong interaction effects, and using lattice quantum chromodynamics to compute the  and B0 meson decay constants5,6,7, are reliably calculated1 in the SM. Their values are
and B0 meson decay constants5,6,7, are reliably calculated1 in the SM. Their values are  and
and  .
.
Many theories that seek to go beyond the standard model (BSM) include new phenomena and particles8,9, such as in the diagrams shown in Fig. 1f and g, that can considerably modify the SM branching fractions. In particular, theories with additional Higgs bosons10,11 predict possible enhancements to the branching fractions. A significant deviation of either of the two branching fraction measurements from the SM predictions would give insight on how the SM should be extended. Alternatively, a measurement compatible with the SM could provide strong constraints on BSM theories.
The ratio of the branching fractions of the two decay modes provides powerful discrimination among BSM theories12. It is predicted in the SM (refs 1, 13 (updates available at http://itpwiki.unibe.ch/), 14, 15 (updated results and plots available at http://www.slac.stanford.edu/xorg/hfag/)) to be  .Notably, BSM theories with the property of minimal flavour violation16 predict the same value as the SM for this ratio.
.Notably, BSM theories with the property of minimal flavour violation16 predict the same value as the SM for this ratio.
The first evidence for the decay  was presented by the LHCb collaboration in 201217. Both CMS and LHCb later published results from all data collected in proton–proton collisions at centre-of-mass energies of 7 TeV in 2011 and 8 TeV in 2012. The measurements had comparable precision and were in good agreement18,19, although neither of the individual results had sufficient precision to constitute the first definitive observation of the
was presented by the LHCb collaboration in 201217. Both CMS and LHCb later published results from all data collected in proton–proton collisions at centre-of-mass energies of 7 TeV in 2011 and 8 TeV in 2012. The measurements had comparable precision and were in good agreement18,19, although neither of the individual results had sufficient precision to constitute the first definitive observation of the  decay to two muons.
decay to two muons.
In this Letter, the two sets of data are combined and analysed simultaneously to exploit fully the statistical power of the data and to account for the main correlations between them. The data correspond to total integrated luminosities of 25 fb−1 and 3 fb−1 for the CMS and LHCb experiments, respectively, equivalent to a total of approximately 1012  and B0 mesons produced in the two experiments together. Assuming the branching fractions given by the SM and accounting for the detection efficiencies, the predicted numbers of decays to be observed in the two experiments together are about 100 for
and B0 mesons produced in the two experiments together. Assuming the branching fractions given by the SM and accounting for the detection efficiencies, the predicted numbers of decays to be observed in the two experiments together are about 100 for  and 10 for B0 → µ+µ−.
and 10 for B0 → µ+µ−.
The CMS20 and LHCb21 detectors are designed to measure SM phenomena with high precision and search for possible deviations. The two collaborations use different and complementary strategies. In addition to performing a broad range of precision tests of the SM and studying the newly-discovered Higgs boson22,23, CMS is designed to search for and study new particles with masses from about 100 GeV/c2 to a few TeV/c2. Since many of these new particles would be able to decay into b quarks and many of the SM measurements also involve b quarks, the detection of b-hadron decays was a key element in the design of CMS. The LHCb collaboration has optimized its detector to study matter–antimatter asymmetries and rare decays of particles containing b quarks, aiming to detect deviations from precise SM predictions that would indicate BSM effects. These different approaches, reflected in the design of the detectors, lead to instrumentation of complementary angular regions with respect to the LHC beams, to operation at different proton–proton collision rates, and to selection of b quark events with different efficiency (for experimental details, see Methods). In general, CMS operates at a higher instantaneous luminosity than LHCb but has a lower efficiency for reconstructing low-mass particles, resulting in a similar sensitivity to LHCb for B0 or  (denoted hereafter by
(denoted hereafter by  ) mesons decaying into two muons.
) mesons decaying into two muons.
Muons do not have strong nuclear interactions and are too massive to emit a substantial fraction of their energy by electromagnetic radiation. This gives them the unique ability to penetrate dense materials, such as steel, and register signals in detectors embedded deep within them. Both experiments use this characteristic to identify muons.
The experiments follow similar data analysis strategies. Decays compatible with  (candidate decays) are found by combining the reconstructed trajectories (tracks) of oppositely charged particles identified as muons. The separation between genuine
(candidate decays) are found by combining the reconstructed trajectories (tracks) of oppositely charged particles identified as muons. The separation between genuine  decays and random combinations of two muons (combinatorial background), most often from semi-leptonic decays of two different b hadrons, is achieved using the dimuon invariant mass,
decays and random combinations of two muons (combinatorial background), most often from semi-leptonic decays of two different b hadrons, is achieved using the dimuon invariant mass,  , and the established characteristics of
, and the established characteristics of  -meson decays. For example, because of their lifetimes of about 1.5 ps and their production at the LHC with momenta between a few GeV/c and ∼100 GeV/c,
-meson decays. For example, because of their lifetimes of about 1.5 ps and their production at the LHC with momenta between a few GeV/c and ∼100 GeV/c,  mesons travel up to a few centimetres before they decay. Therefore, the
mesons travel up to a few centimetres before they decay. Therefore, the  ‘decay vertex’, from which the muons originate, is required to be displaced with respect to the ‘production vertex’, the point where the two protons collide. Furthermore, the negative of the
‘decay vertex’, from which the muons originate, is required to be displaced with respect to the ‘production vertex’, the point where the two protons collide. Furthermore, the negative of the  candidate’s momentum vector is required to point back to the production vertex.
candidate’s momentum vector is required to point back to the production vertex.
These criteria, amongst others that have some ability to distinguish known signal events from background events, are combined into boosted decision trees (BDTs)24,25,26. A BDT is an ensemble of decision trees each placing different selection requirements on the individual variables to achieve the best discrimination between ‘signal-like’ and ‘background-like’ events. Both experiments evaluated many variables for their discriminating power and each chose the best set of about ten to be used in its respective BDT. These include variables related to the quality of the reconstructed tracks of the muons; kinematic variables such as transverse momentum (with respect to the beam axis) of the individual muons and of the  candidate; variables related to the decay vertex topology and fit quality, such as candidate decay length; and isolation variables, which measure the activity in terms of other particles in the vicinity of the two muons or their displaced vertex. A BDT must be ‘trained’ on collections of known background and signal events to generate the selection requirements on the variables and the weights for each tree. In the case of CMS, the background events used in the training are taken from intervals of dimuon mass above and below the signal region in data, while simulated events are used for the signal. The data are divided into disjoint sub-samples and the BDT trained on one sub-sample is applied to a different sub-sample to avoid any bias. LHCb uses simulated events for background and signal in the training of its BDT. After training, the relevant BDT is applied to each event in the data, returning a single value for the event, with high values being more signal-like. To avoid possible biases, both experiments kept the small mass interval that includes both the
candidate; variables related to the decay vertex topology and fit quality, such as candidate decay length; and isolation variables, which measure the activity in terms of other particles in the vicinity of the two muons or their displaced vertex. A BDT must be ‘trained’ on collections of known background and signal events to generate the selection requirements on the variables and the weights for each tree. In the case of CMS, the background events used in the training are taken from intervals of dimuon mass above and below the signal region in data, while simulated events are used for the signal. The data are divided into disjoint sub-samples and the BDT trained on one sub-sample is applied to a different sub-sample to avoid any bias. LHCb uses simulated events for background and signal in the training of its BDT. After training, the relevant BDT is applied to each event in the data, returning a single value for the event, with high values being more signal-like. To avoid possible biases, both experiments kept the small mass interval that includes both the  and B0 signals blind until all selection criteria were established.
and B0 signals blind until all selection criteria were established.
In addition to the combinatorial background, specific b-hadron decays, such as B0 → π−µ+ν where the neutrino cannot be detected and the charged pion is misidentified as a muon, or B0→π0µ+µ−, where the neutral pion in the decay is not reconstructed, can mimic the dimuon decay of the  mesons. The invariant mass of the reconstructed dimuon candidate for these processes (semi-leptonic background) is usually smaller than the mass of the
mesons. The invariant mass of the reconstructed dimuon candidate for these processes (semi-leptonic background) is usually smaller than the mass of the  or B0 meson because the neutrino or another particle is not detected. There is also a background component from hadronic two-body
or B0 meson because the neutrino or another particle is not detected. There is also a background component from hadronic two-body  decays (peaking background) as B0→K+π−, when both hadrons from the decay are misidentified as muons. These misidentified decays can produce peaks in the dimuon invariant-mass spectrum near the expected signal, especially for the B0→µ+µ− decay. Particle identification algorithms are used to minimize the probability that pions and kaons are misidentified as muons, and thus suppress these background sources. Excellent mass resolution is mandatory for distinguishing between B0 and
decays (peaking background) as B0→K+π−, when both hadrons from the decay are misidentified as muons. These misidentified decays can produce peaks in the dimuon invariant-mass spectrum near the expected signal, especially for the B0→µ+µ− decay. Particle identification algorithms are used to minimize the probability that pions and kaons are misidentified as muons, and thus suppress these background sources. Excellent mass resolution is mandatory for distinguishing between B0 and  mesons with a mass difference of about 87 MeV/c2 and for separating them from backgrounds. The mass resolution for
mesons with a mass difference of about 87 MeV/c2 and for separating them from backgrounds. The mass resolution for  decays in CMS ranges from 32 to 75 MeV/c2, depending on the direction of the muons relative to the beam axis, while LHCb achieves a uniform mass resolution of about 25 MeV/c2.
decays in CMS ranges from 32 to 75 MeV/c2, depending on the direction of the muons relative to the beam axis, while LHCb achieves a uniform mass resolution of about 25 MeV/c2.
The CMS and LHCb data are combined by fitting a common value for each branching fraction to the data from both experiments. The branching fractions are determined from the observed numbers, efficiency-corrected, of  mesons that decay into two muons and the total numbers of
mesons that decay into two muons and the total numbers of  mesons produced. Both experiments derive the latter from the number of observed B+→J/ψK+ decays, whose branching fraction has been precisely measured elsewhere14. Assuming equal rates for B+ and B0 production, this gives the normalization for B0 → µ+µ−. To derive the number of
mesons produced. Both experiments derive the latter from the number of observed B+→J/ψK+ decays, whose branching fraction has been precisely measured elsewhere14. Assuming equal rates for B+ and B0 production, this gives the normalization for B0 → µ+µ−. To derive the number of  mesons from this B+ decay mode, the ratio of b quarks that form (hadronize into) B+ mesons to those that form
mesons from this B+ decay mode, the ratio of b quarks that form (hadronize into) B+ mesons to those that form  mesons is also needed. Measurements of this ratio27,28, for which there is additional discussion in Methods, and of the branching fraction
mesons is also needed. Measurements of this ratio27,28, for which there is additional discussion in Methods, and of the branching fraction  (B+ → J/ψ K+) are used to normalize both sets of data and are constrained within Gaussian uncertainties in the fit. The use of these two results by both CMS and LHCb is the only significant source of correlation between their individual branching fraction measurements. The combined fit takes advantage of the larger data sample to increase the precision while properly accounting for the correlation.
(B+ → J/ψ K+) are used to normalize both sets of data and are constrained within Gaussian uncertainties in the fit. The use of these two results by both CMS and LHCb is the only significant source of correlation between their individual branching fraction measurements. The combined fit takes advantage of the larger data sample to increase the precision while properly accounting for the correlation.
In the simultaneous fit to both the CMS and LHCb data, the branching fractions of the two signal channels are common parameters of interest and are free to vary. Other parameters in the fit are considered as nuisance parameters. Those for which additional knowledge is available are constrained to be near their estimated values by using Gaussian penalties with their estimated uncertainties while the others are free to float in the fit. The ratio of the hadronization probability into B+ and  mesons and the branching fraction of the normalization channel B+→J/ψK+ are common, constrained parameters. Candidate decays are categorized according to whether they were detected in CMS or LHCb and to the value of the relevant BDT discriminant. In the case of CMS, they are further categorized according to the data-taking period, and, because of the large variation in mass resolution with angle, whether the muons are both produced at large angles relative to the proton beams (central-region) or at least one muon is emitted at small angle relative to the beams (forward-region). An unbinned extended maximum likelihood fit to the dimuon invariant-mass distribution, in a region of about ±500 MeV/c2 around the
mesons and the branching fraction of the normalization channel B+→J/ψK+ are common, constrained parameters. Candidate decays are categorized according to whether they were detected in CMS or LHCb and to the value of the relevant BDT discriminant. In the case of CMS, they are further categorized according to the data-taking period, and, because of the large variation in mass resolution with angle, whether the muons are both produced at large angles relative to the proton beams (central-region) or at least one muon is emitted at small angle relative to the beams (forward-region). An unbinned extended maximum likelihood fit to the dimuon invariant-mass distribution, in a region of about ±500 MeV/c2 around the  mass, is performed simultaneously in all categories (12 categories from CMS and eight from LHCb). Likelihood contours in the plane of the parameters of interest,
mass, is performed simultaneously in all categories (12 categories from CMS and eight from LHCb). Likelihood contours in the plane of the parameters of interest,  (B0 → µ+µ−) versus
(B0 → µ+µ−) versus  (
( ), are obtained by constructing the test statistic −2ΔlnL from the difference in log-likelihood (lnL) values between fits with fixed values for the parameters of interest and the nominal fit. For each of the two branching fractions, a one-dimensional profile likelihood scan is likewise obtained by fixing only the single parameter of interest and allowing the other to vary during the fits. Additional fits are performed where the parameters under consideration are the ratio of the branching fractions relative to their SM predictions,
), are obtained by constructing the test statistic −2ΔlnL from the difference in log-likelihood (lnL) values between fits with fixed values for the parameters of interest and the nominal fit. For each of the two branching fractions, a one-dimensional profile likelihood scan is likewise obtained by fixing only the single parameter of interest and allowing the other to vary during the fits. Additional fits are performed where the parameters under consideration are the ratio of the branching fractions relative to their SM predictions,  , or the ratio
, or the ratio  of the two branching fractions.
of the two branching fractions.
The combined fit result is shown for all 20 categories in Extended Data Fig. 1. To represent the result of the fit in a single dimuon invariant-mass spectrum, the mass distributions of all categories, weighted according to values of S/(S + B), where S is the expected number of  signals and B is the number of background events under the
signals and B is the number of background events under the  peak in that category, are added together and shown in Fig. 2. The result of the simultaneous fit is overlaid. An alternative representation of the fit to the dimuon invariant-mass distribution for the six categories with the highest S/(S + B) value for CMS and LHCb, as well as displays of events with high probability to be genuine signal decays, are shown in Extended Data Figs 2, 3, 4.
peak in that category, are added together and shown in Fig. 2. The result of the simultaneous fit is overlaid. An alternative representation of the fit to the dimuon invariant-mass distribution for the six categories with the highest S/(S + B) value for CMS and LHCb, as well as displays of events with high probability to be genuine signal decays, are shown in Extended Data Figs 2, 3, 4.
Superimposed on the data points in black are the combined fit (solid blue line) and its components: the  (yellow shaded area) and B0 (light-blue shaded area) signal components; the combinatorial background (dash-dotted green line); the sum of the semi-leptonic backgrounds (dotted salmon line); and the peaking backgrounds (dashed violet line). The horizontal bar on each histogram point denotes the size of the binning, while the vertical bar denotes the 68% confidence interval. See main text for details on the weighting procedure.
(yellow shaded area) and B0 (light-blue shaded area) signal components; the combinatorial background (dash-dotted green line); the sum of the semi-leptonic backgrounds (dotted salmon line); and the peaking backgrounds (dashed violet line). The horizontal bar on each histogram point denotes the size of the binning, while the vertical bar denotes the 68% confidence interval. See main text for details on the weighting procedure.
The combined fit leads to the measurements  where the uncertainties include both statistical and systematic sources, the latter contributing 35% and 18% of the total uncertainty for the
where the uncertainties include both statistical and systematic sources, the latter contributing 35% and 18% of the total uncertainty for the  and B0 signals, respectively. Using Wilks’ theorem29, the statistical significance in unit of standard deviations, σ, is computed to be 6.2 for the
and B0 signals, respectively. Using Wilks’ theorem29, the statistical significance in unit of standard deviations, σ, is computed to be 6.2 for the  decay mode and 3.2 for the B0 → µ+µ− mode. For each signal the null hypothesis that is used to compute the significance includes all background components predicted by the SM as well as the other signal, whose branching fraction is allowed to vary freely. The median expected significances assuming the SM branching fractions are 7.4σ and 0.8σ for the
decay mode and 3.2 for the B0 → µ+µ− mode. For each signal the null hypothesis that is used to compute the significance includes all background components predicted by the SM as well as the other signal, whose branching fraction is allowed to vary freely. The median expected significances assuming the SM branching fractions are 7.4σ and 0.8σ for the  and B0 modes, respectively. Likelihood contours for
and B0 modes, respectively. Likelihood contours for  (B0 → µ+µ−) versus
(B0 → µ+µ−) versus  are shown in Fig. 3. One-dimensional likelihood scans for both decay modes are displayed in the same figure. In addition to the likelihood scan, the statistical significance and confidence intervals for the B0 branching fraction are determined using simulated experiments. This determination yields a significance of 3.0σ for a B0 signal with respect to the same null hypothesis described above. Following the Feldman–Cousins30 procedure, ±1σ and ±2σ confidence intervals for
are shown in Fig. 3. One-dimensional likelihood scans for both decay modes are displayed in the same figure. In addition to the likelihood scan, the statistical significance and confidence intervals for the B0 branching fraction are determined using simulated experiments. This determination yields a significance of 3.0σ for a B0 signal with respect to the same null hypothesis described above. Following the Feldman–Cousins30 procedure, ±1σ and ±2σ confidence intervals for  (B0 → µ+µ−) of [2.5, 5.6] × 10−10 and [1.4, 7.4] × 10−10 are obtained, respectively (see Extended Data Fig. 5).
(B0 → µ+µ−) of [2.5, 5.6] × 10−10 and [1.4, 7.4] × 10−10 are obtained, respectively (see Extended Data Fig. 5).
 (B0→μ+μ−) versus
(B0→μ+μ−) versus  →μ+μ−) plane.
→μ+μ−) plane.The (black) cross in a marks the best-fit central value. The SM expectation and its uncertainty is shown as the (red) marker. Each contour encloses a region approximately corresponding to the reported confidence level. b, c, Variations of the test statistic −2ΔlnL for  (b) and
(b) and  (B0 → µ+µ−) (c). The dark and light (cyan) areas define the ±1σ and ±2σ confidence intervals for the branching fraction, respectively. The SM prediction and its uncertainty for each branching fraction is denoted with the vertical (red) band.
(B0 → µ+µ−) (c). The dark and light (cyan) areas define the ±1σ and ±2σ confidence intervals for the branching fraction, respectively. The SM prediction and its uncertainty for each branching fraction is denoted with the vertical (red) band.
The fit for the ratios of the branching fractions relative to their SM predictions yields  . Associated likelihood contours and one-dimensional likelihood scans are shown in Extended Data Fig. 6. The measurements are compatible with the SM branching fractions of the
. Associated likelihood contours and one-dimensional likelihood scans are shown in Extended Data Fig. 6. The measurements are compatible with the SM branching fractions of the  and B0 → µ+µ− decays at the 1.2σ and 2.2σ level, respectively, when computed from the one-dimensional hypothesis tests. Finally, the fit for the ratio of branching fractions yields
and B0 → µ+µ− decays at the 1.2σ and 2.2σ level, respectively, when computed from the one-dimensional hypothesis tests. Finally, the fit for the ratio of branching fractions yields  which is compatible with the SM at the 2.3σ level. The one-dimensional likelihood scan for this parameter is shown in Fig. 4.
which is compatible with the SM at the 2.3σ level. The one-dimensional likelihood scan for this parameter is shown in Fig. 4.

 →μ+μ−)/
→μ+μ−)/ →μ+μ−).
→μ+μ−).The dark and light (cyan) areas define the ±1σ and ±2σ confidence intervals for  , respectively. The value and uncertainty for
, respectively. The value and uncertainty for  predicted in the SM, which is the same in BSM theories with the minimal flavour violation (MFV) property, is denoted with the vertical (red) band.
predicted in the SM, which is the same in BSM theories with the minimal flavour violation (MFV) property, is denoted with the vertical (red) band.
The combined analysis of data from CMS and LHCb, taking advantage of their full statistical power, establishes conclusively the existence of the  decay and provides an improved measurement of its branching fraction. This concludes a search that started more than three decades ago (see Extended Data Fig. 7), and initiates a phase of precision measurements of the properties of this decay. It also produces three standard deviation evidence for the B0 → µ+µ− decay. The measured branching fractions of both decays are compatible with SM predictions. This is the first time that the CMS and LHCb collaborations have performed a combined analysis of sets of their data in order to obtain a statistically significant observation.
decay and provides an improved measurement of its branching fraction. This concludes a search that started more than three decades ago (see Extended Data Fig. 7), and initiates a phase of precision measurements of the properties of this decay. It also produces three standard deviation evidence for the B0 → µ+µ− decay. The measured branching fractions of both decays are compatible with SM predictions. This is the first time that the CMS and LHCb collaborations have performed a combined analysis of sets of their data in order to obtain a statistically significant observation.
Methods
Experimental setup
At the Large Hadron Collider (LHC), two counter-rotating beams of protons, contained and guided by superconducting magnets spaced around a 27 km circular tunnel, located approximately 100 m underground near Geneva, Switzerland, are brought into collision at four interaction points (IPs). The study presented in this Letter uses data collected at energies of 3.5 TeV per beam in 2011 and 4 TeV per beam in 2012 by the CMS and LHCb experiments located at two of these IPs.
The CMS and LHCb detectors are both designed to look for phenomena beyond the SM (BSM), but using complementary strategies. The CMS detector20, shown in Extended Data Fig. 3, is optimized to search for yet unknown heavy particles, with masses ranging from 100 GeV/c2 to a few TeV/c2, which, if observed, would be a direct manifestation of BSM phenomena. Since many of the hypothesized new particles can decay into particles containing b quarks or into muons, CMS is able to detect efficiently and study B0 (5,280 MeV/c2) and  (5,367 MeV/c2) mesons decaying to two muons even though it is designed to search for particles with much larger masses. The CMS detector covers a very large range of angles and momenta to reconstruct high-mass states efficiently. To that extent, it employs a 13 m long, 6 m diameter superconducting solenoid magnet, operated at a field of 3.8 T, centred on the IP with its axis along the beam direction and covering both hemispheres. A series of silicon tracking layers, consisting of silicon pixel detectors near the beam and silicon strips farther out, organized in concentric cylinders around the beam, extending to a radius of 1.1 m and terminated on each end by planar detectors (disks) perpendicular to the beam, measures the momentum, angles, and position of charged particles emerging from the collisions. Tracking coverage starts from the direction perpendicular to the beam and extends to within 220 mrad from it on both sides of the IP. The inner three cylinders and disks extending from 4.3 to 10.7 cm in radius transverse to the beam are arrays of 100 × 150 µm2 silicon pixels, which can distinguish the displacement of the b-hadron decays from the primary vertex of the collision. The silicon strips, covering radii from 25 cm to approximately 110 cm, have pitches ranging from 80 to 183 µm. The impact parameter is measured with a precision of 10 µm for transverse momenta of 100 GeV/c and 20 µm for 10 GeV/c. The momentum resolution, provided mainly by the silicon strips, changes with the angle relative to the beam direction, resulting in a mass resolution for
(5,367 MeV/c2) mesons decaying to two muons even though it is designed to search for particles with much larger masses. The CMS detector covers a very large range of angles and momenta to reconstruct high-mass states efficiently. To that extent, it employs a 13 m long, 6 m diameter superconducting solenoid magnet, operated at a field of 3.8 T, centred on the IP with its axis along the beam direction and covering both hemispheres. A series of silicon tracking layers, consisting of silicon pixel detectors near the beam and silicon strips farther out, organized in concentric cylinders around the beam, extending to a radius of 1.1 m and terminated on each end by planar detectors (disks) perpendicular to the beam, measures the momentum, angles, and position of charged particles emerging from the collisions. Tracking coverage starts from the direction perpendicular to the beam and extends to within 220 mrad from it on both sides of the IP. The inner three cylinders and disks extending from 4.3 to 10.7 cm in radius transverse to the beam are arrays of 100 × 150 µm2 silicon pixels, which can distinguish the displacement of the b-hadron decays from the primary vertex of the collision. The silicon strips, covering radii from 25 cm to approximately 110 cm, have pitches ranging from 80 to 183 µm. The impact parameter is measured with a precision of 10 µm for transverse momenta of 100 GeV/c and 20 µm for 10 GeV/c. The momentum resolution, provided mainly by the silicon strips, changes with the angle relative to the beam direction, resulting in a mass resolution for  decays that varies from 32 MeV/c2 for
decays that varies from 32 MeV/c2 for  mesons produced perpendicularly to the proton beams to 75 MeV/c2 for those produced at small angles relative to the beam direction. After the tracking system, at a greater distance from the IP, there is a calorimeter that stops (absorbs) all particles except muons and measures their energies. The calorimeter consists of an electromagnetic section followed by a hadronic section. Muons are identified by their ability to penetrate the calorimeter and the steel return yoke of the solenoid magnet and to produce signals in gas-ionization particle detectors located in compartments within the steel yoke. The CMS detector has no capability to discriminate between charged hadron species, pions, kaons, or protons, that is effective at the typical particle momenta in this analysis.
mesons produced perpendicularly to the proton beams to 75 MeV/c2 for those produced at small angles relative to the beam direction. After the tracking system, at a greater distance from the IP, there is a calorimeter that stops (absorbs) all particles except muons and measures their energies. The calorimeter consists of an electromagnetic section followed by a hadronic section. Muons are identified by their ability to penetrate the calorimeter and the steel return yoke of the solenoid magnet and to produce signals in gas-ionization particle detectors located in compartments within the steel yoke. The CMS detector has no capability to discriminate between charged hadron species, pions, kaons, or protons, that is effective at the typical particle momenta in this analysis.
The primary commitment of the LHCb collaboration is the study of particle–antiparticle asymmetries and of rare decays of particles containing b and c quarks. LHCb aims at detecting BSM particles indirectly by measuring their effect on b-hadron properties for which precise SM predictions exist. The production cross section of b hadrons at the LHC is particularly large at small angles relative to the colliding beams. The small-angle region also provides advantages for the detection and reconstruction of a wide range of their decays. The LHCb experiment21, shown in Extended Data Fig. 4, instruments the angular interval from 10 to 300 mrad with respect to the beam direction on one side of the interaction region. Its detectors are designed to reconstruct efficiently a wide range of b-hadron decays, resulting in charged pions and kaons, protons, muons, electrons, and photons in the final state. The detector includes a high-precision tracking system consisting of a silicon strip vertex detector, a large-area silicon strip detector located upstream of a dipole magnet characterized by a field integral of 4 T m, and three stations of silicon strip detectors and straw drift tubes downstream of the magnet. The vertex detector has sufficient spatial resolution to distinguish the slight displacement of the weakly decaying b hadron from the primary production vertex where the two protons collided and produced it. The tracking detectors upstream and downstream of the dipole magnet measure the momenta of charged particles. The combined tracking system provides a momentum measurement with an uncertainty that varies from 0.4% at 5 GeV/c to 0.6% at 100 GeV/c. This results in an invariant-mass resolution of 25 MeV/c2 for  mesons decaying to two muons that is nearly independent of the angle with respect to the beam. The impact parameter resolution is smaller than 20 µm for particle tracks with large transverse momentum. Different types of charged hadrons are distinguished by information from two ring-imaging Cherenkov detectors. Photon, electron, and hadron candidates are identified by calorimeters. Muons are identified by a system composed of alternating layers of iron and multiwire proportional chambers.
mesons decaying to two muons that is nearly independent of the angle with respect to the beam. The impact parameter resolution is smaller than 20 µm for particle tracks with large transverse momentum. Different types of charged hadrons are distinguished by information from two ring-imaging Cherenkov detectors. Photon, electron, and hadron candidates are identified by calorimeters. Muons are identified by a system composed of alternating layers of iron and multiwire proportional chambers.
Neither CMS nor LHCb records all the interactions occurring at its IP because the data storage and analysis costs would be prohibitive. Since most of the interactions are reasonably well characterized (and can be further studied by recording only a small sample of them) specific event filters (known as triggers) select the rare processes that are of interest to the experiments. Both CMS and LHCb implement triggers that specifically select events containing two muons. The triggers of both experiments have a hardware stage, based on information from the calorimeter and muon systems, followed by a software stage, consisting of a large computing cluster that uses all the information from the detector, including the tracking, to make the final selection of events to be recorded for subsequent analysis. Since CMS is designed to look for much heavier objects than  mesons, it selects events that contain muons with higher transverse momenta than those selected by LHCb. This eliminates many of the
mesons, it selects events that contain muons with higher transverse momenta than those selected by LHCb. This eliminates many of the  decays while permitting CMS to run at a higher proton–proton collision rate to look for the more rare massive particles. Thus CMS runs at higher collision rates but with lower efficiency than LHCb for
decays while permitting CMS to run at a higher proton–proton collision rate to look for the more rare massive particles. Thus CMS runs at higher collision rates but with lower efficiency than LHCb for  mesons decaying to two muons. The overall sensitivity to these decays turns out to be similar in the two experiments.
mesons decaying to two muons. The overall sensitivity to these decays turns out to be similar in the two experiments.
CMS and LHCb are not the only collaborations to have searched for  and B0→ µ+ µ− decays. Over three decades, a total of eleven collaborations have taken part in this search14, as illustrated by Extended Data Fig. 7. This plot gathers the results from CLEO31,32,33,34,35, ARGUS36, UA137,38, CDF39,40,41,42,43,44, L345, DØ46,47,48,49,50, Belle51, Babar52,53, LHCb17,54,55,56,57 CMS18,58,59 and ATLAS60.
and B0→ µ+ µ− decays. Over three decades, a total of eleven collaborations have taken part in this search14, as illustrated by Extended Data Fig. 7. This plot gathers the results from CLEO31,32,33,34,35, ARGUS36, UA137,38, CDF39,40,41,42,43,44, L345, DØ46,47,48,49,50, Belle51, Babar52,53, LHCb17,54,55,56,57 CMS18,58,59 and ATLAS60.
Analysis description
The analysis techniques used to obtain the results presented in this Letter are very similar to those used to obtain the individual result in each collaboration, described in more detail in refs 18, 19. Here only the main analysis steps are reviewed and the changes used in the combined analysis are highlighted. Data samples for this analysis were collected by the two experiments in proton–proton collisions at a centre-of-mass energy of 7 and 8 TeV during 2011 and 2012, respectively. These samples correspond to a total integrated luminosity of 25 and 3 fb−1 for the CMS and LHCb experiments, respectively, and represent their complete data sets from the first running period of the LHC.
The trigger criteria were slightly different between the two experiments. The large majority of events were triggered by requirements on one or both muons of the signal decay: the LHCb detector triggered on muons with transverse momentum pT > 1.5 GeV/c while the CMS detector, because of its geometry and higher instantaneous luminosity, triggered on two muons with pT > 4(3) GeV/c, for the leading (sub-leading) muon.
The data analysis procedures in the two experiments follow similar strategies. Pairs of high-quality oppositely charged particle tracks that have one of the expected patterns of hits in the muon detectors are fitted to form a common vertex in three dimensions, which is required to be displaced from the primary interaction vertex (PV) and to have a small χ2 in the fit. The resulting  candidate is further required to point back to the PV, for example, to have a small impact parameter, consistent with zero, with respect to it. The final classification of data events is done in categories of the response of a multivariate discriminant (MVA) combining information from the kinematics and vertex topology of the events. The type of MVA used is a boosted decision tree (BDT)24,25,26. The branching fractions are then obtained by a fit to the dimuon invariant mass,
candidate is further required to point back to the PV, for example, to have a small impact parameter, consistent with zero, with respect to it. The final classification of data events is done in categories of the response of a multivariate discriminant (MVA) combining information from the kinematics and vertex topology of the events. The type of MVA used is a boosted decision tree (BDT)24,25,26. The branching fractions are then obtained by a fit to the dimuon invariant mass,  , of all categories simultaneously.
, of all categories simultaneously.
The signals appear as peaks at the  and B0 masses in the invariant-mass distributions, observed over background events. One of the components of the background is combinatorial in nature, as it is due to the random combinations of genuine muons. These produce a smooth dimuon mass distribution in the vicinity of the
and B0 masses in the invariant-mass distributions, observed over background events. One of the components of the background is combinatorial in nature, as it is due to the random combinations of genuine muons. These produce a smooth dimuon mass distribution in the vicinity of the  and B0 masses, estimated in the fit to the data by extrapolation from the sidebands of the invariant-mass distribution. In addition to the combinatorial background, certain specific b-hadron decays can mimic the signal or contribute to the background in its vicinity. In particular, the semi-leptonic decays B0 → π−µ+ν,
and B0 masses, estimated in the fit to the data by extrapolation from the sidebands of the invariant-mass distribution. In addition to the combinatorial background, certain specific b-hadron decays can mimic the signal or contribute to the background in its vicinity. In particular, the semi-leptonic decays B0 → π−µ+ν,  → K−µ+ν, and
→ K−µ+ν, and  can have reconstructed masses that are near the signal if one of the hadrons is misidentified as a muon and is combined with a genuine muon. Similarly the dimuon coming from the rare B0 → π0µ+µ− and B+ → π+µ+µ− decays can also fake the signal. All these background decays, when reconstructed as a dimuon final state, have invariant masses that are lower than the masses of the B0 and
can have reconstructed masses that are near the signal if one of the hadrons is misidentified as a muon and is combined with a genuine muon. Similarly the dimuon coming from the rare B0 → π0µ+µ− and B+ → π+µ+µ− decays can also fake the signal. All these background decays, when reconstructed as a dimuon final state, have invariant masses that are lower than the masses of the B0 and  mesons, because they are missing one of the original decay particles. An exception is the decay
mesons, because they are missing one of the original decay particles. An exception is the decay  , which can also populate, with a smooth mass distribution, higher-mass regions. Furthermore, background due to misidentified hadronic two-body decays
, which can also populate, with a smooth mass distribution, higher-mass regions. Furthermore, background due to misidentified hadronic two-body decays  , where
, where  or K, is present when both hadrons are misidentified as muons. These misidentified decays produce an apparent dimuon invariant-mass peak close to the B0 mass value. Such a peak can mimic a B0 → µ+µ− signal and is estimated from control channels and added to the fit.
or K, is present when both hadrons are misidentified as muons. These misidentified decays produce an apparent dimuon invariant-mass peak close to the B0 mass value. Such a peak can mimic a B0 → µ+µ− signal and is estimated from control channels and added to the fit.
The distributions of signal in the invariant mass and in the MVA discriminant are derived from simulations with a detailed description of the detector response for CMS and are calibrated using exclusive two-body hadronic decays in data for LHCb. The distributions for the backgrounds are obtained from simulation with the exception of the combinatorial background. The latter is obtained by interpolating from the data invariant-mass sidebands separately for each category, after the subtraction of the other background components.
To compute the signal branching fractions, the numbers of  and B0 mesons that are produced, as well as the numbers of those that have decayed into a dimuon pair, are needed. The latter numbers are the raw results of this analysis, whereas the former need to be determined from measurements of one or more ‘normalization’ decay channels, which are abundantly produced, have an absolute branching fraction that is already known with good precision, and that share characteristics with the signals, so that their trigger and selection efficiencies do not differ significantly. Both experiments use the B+ → J/ψK+ decay as a normalization channel with
and B0 mesons that are produced, as well as the numbers of those that have decayed into a dimuon pair, are needed. The latter numbers are the raw results of this analysis, whereas the former need to be determined from measurements of one or more ‘normalization’ decay channels, which are abundantly produced, have an absolute branching fraction that is already known with good precision, and that share characteristics with the signals, so that their trigger and selection efficiencies do not differ significantly. Both experiments use the B+ → J/ψK+ decay as a normalization channel with  (B+ → J/ψ (µ+µ−) K+) = (6.10 ± 0.19) × 10−5, and LHCb also uses the B0 → K+π− channel with
(B+ → J/ψ (µ+µ−) K+) = (6.10 ± 0.19) × 10−5, and LHCb also uses the B0 → K+π− channel with  (B0 → K+π−) = (1.96 ± 0.05) × 10−5. Both branching fraction values are taken from ref. 14. Hence, the
(B0 → K+π−) = (1.96 ± 0.05) × 10−5. Both branching fraction values are taken from ref. 14. Hence, the  → µ+µ− branching fraction is expressed as a function of the number of signal events
→ µ+µ− branching fraction is expressed as a function of the number of signal events  in the data normalized to the numbers of B+ → J/ψK+ and B0 → K+π− events:
in the data normalized to the numbers of B+ → J/ψK+ and B0 → K+π− events:

where the ‘norm.’ subscript refers to either of the normalization channels. The values of the normalization parameter αnorm. obtained by LHCb from the two normalization channels are found in good agreement and their weighted average is used. In this formula ε indicates the total event detection efficiency including geometrical acceptance, trigger selection, reconstruction, and analysis selection for the corresponding decay. The fd/fs factor is the ratio of the probabilities for a b quark to hadronize into a B0 as compared to a  meson; the probability to hadronize into a B+ (fu) is assumed to be equal to that into B0 (fd) on the basis of theoretical grounds, and this assumption is checked on data. The value of fd/fs = 3.86 ± 0.22 measured by LHCb27,28,61 is used in this analysis. As the value of fd/fs depends on the kinematic range of the considered particles, which differs between LHCb and CMS, CMS checked this observable with the decays
meson; the probability to hadronize into a B+ (fu) is assumed to be equal to that into B0 (fd) on the basis of theoretical grounds, and this assumption is checked on data. The value of fd/fs = 3.86 ± 0.22 measured by LHCb27,28,61 is used in this analysis. As the value of fd/fs depends on the kinematic range of the considered particles, which differs between LHCb and CMS, CMS checked this observable with the decays  and B+ → J/ψK+ within its acceptance, finding a consistent value. An additional systematic uncertainty of 5% was assigned to fd/fs to account for the extrapolation of the LHCb result to the CMS acceptance. An analogous formula to that in equation (1) holds for the normalization of the B0 → µ+µ− decay, with the notable difference that the fd/fs factor is replaced by fd/fu = 1.
and B+ → J/ψK+ within its acceptance, finding a consistent value. An additional systematic uncertainty of 5% was assigned to fd/fs to account for the extrapolation of the LHCb result to the CMS acceptance. An analogous formula to that in equation (1) holds for the normalization of the B0 → µ+µ− decay, with the notable difference that the fd/fs factor is replaced by fd/fu = 1.
The antiparticle  and the particle B0 (
and the particle B0 ( ) can both decay into two muons and no attempt is made in this analysis to determine whether the antiparticle or particle was produced (untagged method). However, the B0 and
) can both decay into two muons and no attempt is made in this analysis to determine whether the antiparticle or particle was produced (untagged method). However, the B0 and  particles are known to oscillate, that is to transform continuously into their antiparticles and vice versa. Therefore, a quantum superposition of particle and antiparticle states propagates in the laboratory before decaying. This superposition can be described by two ‘mass eigenstates’, which are symmetric and antisymmetric in the charge-parity (CP) quantum number, and have slightly different masses. In the SM, the heavy eigenstate can decay into two muons, whereas the light eigenstate cannot without violating the CP quantum number conservation. In BSM models, this is not necessarily the case. In addition to their masses, the two eigenstates of the
particles are known to oscillate, that is to transform continuously into their antiparticles and vice versa. Therefore, a quantum superposition of particle and antiparticle states propagates in the laboratory before decaying. This superposition can be described by two ‘mass eigenstates’, which are symmetric and antisymmetric in the charge-parity (CP) quantum number, and have slightly different masses. In the SM, the heavy eigenstate can decay into two muons, whereas the light eigenstate cannot without violating the CP quantum number conservation. In BSM models, this is not necessarily the case. In addition to their masses, the two eigenstates of the  system also differ in their lifetime values14. The lifetimes of the light and heavy eigenstates are also different from the average
system also differ in their lifetime values14. The lifetimes of the light and heavy eigenstates are also different from the average  lifetime, which is used by CMS and LHCb in the simulations of signal decays. Since the information on the displacement of the secondary decay with respect to the PV is used as a discriminant against combinatorial background in the analysis, the efficiency versus lifetime has a model-dependent bias62 that must be removed. This bias is estimated assuming SM dynamics. Owing to the smaller difference between the lifetime of its heavy and light mass eigenstates, no correction is required for the B0 decay mode.
lifetime, which is used by CMS and LHCb in the simulations of signal decays. Since the information on the displacement of the secondary decay with respect to the PV is used as a discriminant against combinatorial background in the analysis, the efficiency versus lifetime has a model-dependent bias62 that must be removed. This bias is estimated assuming SM dynamics. Owing to the smaller difference between the lifetime of its heavy and light mass eigenstates, no correction is required for the B0 decay mode.
Detector simulations are needed by both CMS and LHCb. CMS relies on simulated events to determine resolutions and trigger and reconstruction efficiencies, and to provide the signal sample for training the BDT. The dimuon mass resolution given by the simulation is validated using data on J/ψ, Υ, and Z-boson decays to two muons. The tracking and trigger efficiencies obtained from the simulation are checked using special control samples from data. The LHCb analysis is designed to minimize the impact of discrepancies between simulations and data. The mass resolution is measured with data. The distribution of the BDT for the signal and for the background is also calibrated with data using control channels and mass sidebands. The efficiency ratio for the trigger is also largely determined from data. The simulations are used to determine the efficiency ratios of selection and reconstruction processes between signal and normalization channels. As for the overall detector simulation, each experiment has a team dedicated to making the simulations as complete and realistic as possible. The simulated data are constantly being compared to the actual data. Agreement between simulation and data in both experiments is quite good, often extending well beyond the cores of distributions. Differences occur because, for example, of incomplete description of the material of the detectors, approximations made to keep the computer time manageable, residual uncertainties in calibration and alignment, and discrepancies or limitations in the underlying theory and experimental data used to model the relevant collisions and decays. Small differences between simulation and data that are known to have an impact on the result are treated either by reweighting the simulations to match the data or by assigning appropriate systematic uncertainties.
Small changes are made to the analysis procedure with respect to refs 18, 19 in order to achieve a consistent combination between the two experiments. In the LHCb analysis, the  background component, which was not included in the fit for the previous result but whose effect was accounted for as an additional systematic uncertainty, is now included in the standard fit. The following modifications are made to the CMS analysis: the
background component, which was not included in the fit for the previous result but whose effect was accounted for as an additional systematic uncertainty, is now included in the standard fit. The following modifications are made to the CMS analysis: the  branching fraction is updated to a more recent prediction63,64 of
branching fraction is updated to a more recent prediction63,64 of  ; the phase space model of the decay
; the phase space model of the decay  is changed to a more appropriate semi-leptonic decay model63; and the decay time bias correction for the
is changed to a more appropriate semi-leptonic decay model63; and the decay time bias correction for the  , previously absent from the analysis, is now calculated and applied with a different correction for each category of the multivariate discriminant.
, previously absent from the analysis, is now calculated and applied with a different correction for each category of the multivariate discriminant.
These modifications result in changes in the individual results of each experiment. The modified CMS analysis, applied on the CMS data, yields

while the LHCb results change to

These results are only slightly different from the published ones and are in agreement with each other.
Simultaneous fit
The goal of the analysis presented in this Letter is to combine the full data sets of the two experiments to reduce the uncertainties on the branching fractions of the signal decays obtained from the individual determinations. A simultaneous unbinned extended maximum likelihood fit is performed to the data of the two experiments, using the invariant-mass distributions of all 20 MVA discriminant categories of both experiments. The invariant-mass distributions are defined in the dimuon mass ranges  ∈[4.9, 5.9] GeV/c2 and [4.9, 6.0] GeV/c2 for the CMS and LHCb experiments, respectively. The branching fractions of the signal decays, the hadronization fraction ratio fd/fs, and the branching fraction of the normalization channel B+ → J/ψK+ are treated as common parameters. The value of the B+ → J/ψK+ branching fraction is the combination of results from five different experiments14, taking advantage of all their data to achieve the most precise input parameters for this analysis. The combined fit takes advantage of the larger data sample and proper treatment of the correlations between the individual measurements to increase the precision and reliability of the result, respectively.
∈[4.9, 5.9] GeV/c2 and [4.9, 6.0] GeV/c2 for the CMS and LHCb experiments, respectively. The branching fractions of the signal decays, the hadronization fraction ratio fd/fs, and the branching fraction of the normalization channel B+ → J/ψK+ are treated as common parameters. The value of the B+ → J/ψK+ branching fraction is the combination of results from five different experiments14, taking advantage of all their data to achieve the most precise input parameters for this analysis. The combined fit takes advantage of the larger data sample and proper treatment of the correlations between the individual measurements to increase the precision and reliability of the result, respectively.
Fit parameters, other than those of primary physics interest, whose limited knowledge affects the results, are called ‘nuisance parameters’. In particular, systematic uncertainties are modelled by introducing nuisance parameters into the statistical model and allowing them to vary in the fit; those for which additional knowledge is present are constrained using Gaussian distributions. The mean and standard deviation of these distributions are set to the central value and uncertainty obtained either from other measurements or from control channels. The statistical component of the final uncertainty on the branching fractions is obtained by repeating the fit after fixing all of the constrained nuisance parameters to their best fitted values. The systematic component is then calculated by subtracting in quadrature the statistical component from the total uncertainty. In addition to the free fit, a two-dimensional likelihood ratio scan in the plane  (B0 → µ+µ−) versus
(B0 → µ+µ−) versus  is performed.
is performed.
Feldman–Cousins confidence interval
The Feldman–Cousins likelihood ratio ordering procedure30 is a unified frequentist method to construct single- and double-sided confidence intervals for parameters of a given model adapted to the data. It provides a natural transition between single-sided confidence intervals, used to define upper or lower limits, and double-sided ones. Since the single-experiment results18,19 showed that the B0 → µ+µ− signal is at the edge of the probability region customarily used to assert statistically significant evidence for a result, a Feldman–Cousins procedure is performed. This allows a more reliable determination of the confidence interval and significance of this signal without the assumptions required for the use of Wilks’ theorem. In addition, a prescription for the treatment of nuisance parameters has to be chosen because scanning the whole parameter space in the presence of more than a few parameters is computationally too intensive. In this case the procedure described by the ATLAS and CMS Higgs combination group65 is adopted. For each point of the space of the relevant parameters, the nuisance parameters are fixed to their best value estimated by the mean of a maximum likelihood fit to the data with the value of  (B0 → µ+µ−) fixed and all nuisance parameters profiled with Gaussian penalties. Sampling distributions are constructed for each tested point of the parameter of interest by generating simulated experiments and performing maximum likelihood fits in which the Gaussian mean values of the external constraints on the nuisance parameters are randomized around the best-fit values for the nuisance parameters used to generate the simulated experiments. The sampling distribution is constructed from the distribution of the negative log-likelihood ratio evaluated on the simulated experiments by performing one likelihood fit in which the value of
(B0 → µ+µ−) fixed and all nuisance parameters profiled with Gaussian penalties. Sampling distributions are constructed for each tested point of the parameter of interest by generating simulated experiments and performing maximum likelihood fits in which the Gaussian mean values of the external constraints on the nuisance parameters are randomized around the best-fit values for the nuisance parameters used to generate the simulated experiments. The sampling distribution is constructed from the distribution of the negative log-likelihood ratio evaluated on the simulated experiments by performing one likelihood fit in which the value of  (B0 → µ+µ−) is free to float and another with the
(B0 → µ+µ−) is free to float and another with the  (B0 → µ+µ−) fixed to the tested point value. This sampling distribution is then converted to a confidence level by evaluating the fraction of simulated experiments entries with a value for the negative log-likelihood ratio greater than or equal to the value observed in the data for each tested point. The results of this procedure are shown in Extended Data Fig. 5.
(B0 → µ+µ−) fixed to the tested point value. This sampling distribution is then converted to a confidence level by evaluating the fraction of simulated experiments entries with a value for the negative log-likelihood ratio greater than or equal to the value observed in the data for each tested point. The results of this procedure are shown in Extended Data Fig. 5.
References
Bobeth, C. et al. B s,d → l+l− in the Standard Model with reduced theoretical uncertainty. Phys. Rev. Lett. 112, 101801 (2014)
Evans, L. & Bryant, P. LHC machine. J. Instrum. 3, S08001 (2008)
Planck Collaboration, P. A. R. et al. Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 571, A16 (2014)
Gavela, M., Lozano, M., Orloff, J. & Pène, O. Standard model CP-violation and baryon asymmetry (I). Zero temperature. Nucl. Phys. B 430, 345–381 (1994)
RBC–UKQCD Collaborations, Witzel, O. B-meson decay constants with domain-wall light quarks and nonperturbatively tuned relativistic b-quarks. Preprint at http://arXiv.org/abs/1311.0276 (2013)
HPQCD Collaboration, Na, H. et al. B and B s meson decay constants from lattice QCD. Phys. Rev. D 86, 034506 (2012)
Fermilab Lattice and MILC Collaborations, Bazavov, A. et al. B- and D-meson decay constants from three-flavor lattice QCD. Phys. Rev. D 85, 114506 (2012)
Huang, C.-S., Liao, W. & Yan, Q.-S. The promising process to distinguish super-symmetric models with large tanβ from the standard model: B → X s µ+µ−. Phys. Rev. D 59, 011701 (1998)
Rai Choudhury, S. & Gaur, N. Dileptonic decay of B s meson in SUSY models with large tan β. Phys. Lett. B 451, 86–92 (1999)
Babu, K. & Kolda, C. F. Higgs-mediated B0 → µ+µ− in minimal supersymmetry. Phys. Rev. Lett. 84, 228–231 (2000)
Bobeth, C., Ewerth, T., Kruger, F. & Urban, J. Analysis of neutral Higgs-boson contributions to the decays and . Phys. Rev. D 64, 074014 (2001)
Buras, A. J. Relations between ΔM s,d and B s,d → µ in models with minimal flavor violation. Phys. Lett. B 566, 115–119 (2003)
Aoki, S. et al. Review of lattice results concerning low-energy particle physics. Eur. Phys. J. C 74, 2890 (2014)
Particle Data Group, Beringer, J. et al. Review of particle physics. Phys. Rev. D 86, 010001 (2012); 2013 partial update for the 2014 edition at http://pdg.lbl.gov
Heavy Flavor Averaging Group, Amhis, Y. et al. Averages of b-hadron, c-hadron, and τ-lepton properties as of early 2012. Preprint at http://arXiv.org/abs/1207.1158 (2012)
D’Ambrosio, G., Giudice, G. F., Isidori, G. & Strumia, A. Minimal flavour violation: an effective field theory approach. Nucl. Phys. B 645, 155–187 (2002)
LHCb Collaboration, Aaij, R. et al. First evidence for the decay . Phys. Rev. Lett. 110, 021801 (2013)
CMS Collaboration, Chatrchyan, S. et al. Measurement of the branching fraction and search for with the CMS experiment. Phys. Rev. Lett. 111, 101804 (2013)
LHCb Collaboration, Aaij, R. et al. Measurement of the branching fraction and search for decays at the LHCb experiment. Phys. Rev. Lett. 111, 101805 (2013)
CMS Collaboration, Chatrchyan, S. et al. The CMS experiment at the CERN LHC. J. Instrum. 3, S08004 (2008)
LHCb Collaboration, Alves, A. A. Jr et al. The LHCb detector at the LHC. J. Instrum. 3, S08005 (2008)
ATLAS Collaboration, Aad, G. et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 716, 1–29 (2012)
CMS Collaboration, Chatrchyan, S. et al. Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B 716, 30–61 (2012)
Breiman, L., Friedman, J. H., Olshen, R. A. & Stone, C. J. Classification and Regression Trees (Wadsworth International Group, 1984)
Freund, Y. & Schapire, R. E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 55, 119–139 (1997)
Hoecker, A. et al. TMVA: Toolkit for Multivariate Data Analysis. Proc. Sci. Adv. Comput. Anal. Techn. Phys. Res.. 040 http://pos.sissa.it/archive/conferences/050/040/ACAT_040.pdf (2007)
LHCb Collaboration, Aaij, R. et al. Measurement of b hadron production fractions in 7 TeV pp collisions. Phys. Rev. D 85, 032008 (2012)
LHCb Collaboration, Aaij, R. et al. Measurement of the fragmentation fraction ratio f s /f d and its dependence on B meson kinematics. J. High Energy Phys. 4, 1 (2013); updated in https://cds.cern.ch/record/1559262/files/LHCb-CONF-2013-011.pdf
Wilks, S. S. The large-sample distribution of the likelihood ratio for testing composite hypotheses. Ann. Math. Stat. 9, 60–62 (1938)
Feldman, G. J. & Cousins, R. D. Unified approach to the classical statistical analysis of small signals. Phys. Rev. D 57, 3873–3889 (1998)
CLEO Collaboration, Giles, R. et al. Two-body decays of B mesons. Phys. Rev. D 30, 2279–2294 (1984)
CLEO Collaboration, Avery, P. et al. Limits on rare exclusive decays of B mesons. Phys. Lett. B 183, 429–433 (1987)
CLEO Collaboration, Avery, P. et al. A search for exclusive penguin decays of B mesons. Phys. Lett. B 223, 470–475 (1989)
CLEO Collaboration, Ammar, R. et al. Search for B0 decays to two charged leptons. Phys. Rev. D 49, 5701–5704 (1994)
CLEO Collaboration, Bergfeld, T. et al. Search for decays of B0 mesons into pairs of leptons: B0 → e+e−, B0 → µ+µ− and B0 → e±µ∓. Phys. Rev. D 62, 091102 (2000)
ARGUS Collaboration, Albrecht, H. et al. B meson decays into charmonium states. Phys. Lett. B 199, 451–456 (1987)
UA1 Collaboration, Albajar, C. et al. Low mass dimuon production at the CERN proton-antiproton collider. Phys. Lett. B 209, 397–406 (1988)
UA1 Collaboration, Albajar C. et al. A search for rare B meson decays at the CERN Sp S collider. Phys. Lett. B 262, 163–170 (1991)
CDF Collaboration, Abe, F. et al. Search for flavor-changing neutral current B meson decays in p collisions at = 1.8 TeV. Phys. Rev. Lett. 76, 4675–4680 (1996)
CDF Collaboration, Abe, F. et al. Search for the decays and in p collisions at = 1.8 TeV. Phys. Rev. D 57, 3811–3816 (1998)
CDF Collaboration, Acousta, D. et al. Search for and decays in p collisions at = 1.96 TeV. Phys. Rev. Lett. 93, 032001 (2004)
CDF Collaboration, Abulencia, A. et al. Search for B s → µ+µ− and B d → µ+µ− decays in p collisions with CDF II. Phys. Rev. Lett. 95, 221805 (2005)
CDF Collaboration, Aaltonen, T. et al. Search for B s → µ+µ− and B d → µ+µ– decays with CDF II. Phys. Rev. Lett. 107, 191801 (2011)
CDF Collaboration, Aaltonen, T. et al. Search for B s → µ+µ− and B d → µ+µ− decays with the full CDF Run II data set. Phys. Rev. D 87, 072003 (2013)
L3 Collaboration, Acciarri, M. et al. Search for neutral B meson decays to two charged leptons. Phys. Lett. B 391, 474–480 (1997)
DØ Collaboration, Abbott, B. et al. Search for the decay b → X s µ+µ−. Phys. Lett. B 423, 419–426 (1998)
DØ Collaboration, Abazov, V. et al. A search for the flavor-changing neutral current decay in collisions at = 1.96 TeV with the DØ detector. Phys. Rev. Lett. 94, 071802 (2005)
DØ Collaboration, Abazov, V. M. et al. Search for at DØ. Phys. Rev. D 76, 092001 (2007)
DØ Collaboration, Abazov, V. M. et al. Search for the rare decay . Phys. Lett. B 693, 539–544 (2010)
DØ Collaboration, Abazov, V. M. et al. Search for the rare decay . Phys. Rev. D 87, 072006 (2013)
BELLE Collaboration, Chang, M. et al. Search for B0 → ℓ+ℓ− at BELLE. Phys. Rev. D 68, 111101 (2003)
BaBar Collaboration, Aubert, B. et al. Search for decays of B0 mesons into pairs of charged leptons: B0 → e+e−, B0 → µ+µ−, B0 → e±µ∓. Phys. Rev. Lett. 94, 221803 (2005)
BaBar Collaboration, Aubert, B. et al. Search for decays of B0 mesons into e+e−, µ+µ−, and e±µ∓ final states. Phys. Rev. D 77, 032007 (2008)
LHCb Collaboration, Aaij, R. et al. Search for the rare decays and B0 → µ+µ−. Phys. Lett. B 699, 330–340 (2011)
LHCb Collaboration, Aaij, R. et al. Strong constraints on the rare decays →µ+µ− and B0 → µ+µ−. Phys. Rev. Lett. 108, 231801 (2012)
LHCb Collaboration, Aaij, R. et al. Search for the rare decays and B0 → µ+µ−. Phys. Lett. B 708, 55–67 (2012)
LHCb Collaboration, Aaij, R. et al. Measurement of the branching fraction and search for B0 → µ+µ− decays at the LHCb experiment. Phys. Rev. Lett. 111, 101805 (2013)
CMS Collaboration, Chatrchyan, S. et al. Search for and B0 → µ+µ− decays in pp collisions at 7 TeV. Phys. Rev. Lett. 107, 191802 (2011)
CMS Collaboration, Chatrchyan, S. et al. Search for and B0 → µ+µ− decays. J. High Energy Phys. 04, 033 (2012)
ATLAS Collaboration, Aad, G. et al. Search for the decay with the ATLAS detector. Phys. Lett. B 713, 387–407 (2012)
LHCb Collaboration, Aaij, R. et al. Updated average f s /f d b-hadron production fraction ratio for 7 TeV pp collisions. http://cds.cern.ch/record/1559262 (LHCb-CONF-2013-011, 2013)
De Bruyn, K. et al. Probing new physics via the effective lifetime. Phys. Rev. Lett. 109, 041801 (2012)
Khodjamirian, A., Klein, C., Mannel, T. & Wang, Y.-M. Form factors and strong couplings of heavy baryons from QCD light-cone sum rules. J. High Energy Phys. 09, 106 (2011)
LHCb Collaboration, Aaij R. et al. Precision measurement of the ratio of the to lifetimes. Phys. Lett. B 734, 122–130 (2014)
ATLAS and CMS Collaborations. Procedure for the LHC Higgs boson search combination in summer 2011. http://cds.cern.ch/record/1379837 (ATL-PHYS-PUB-2011-011, CMS NOTE 2011/005, 2011)
Acknowledgements
We express our gratitude to colleagues in the CERN accelerator departments for the excellent performance of the LHC. We thank the technical and administrative staff at CERN, at the CMS institutes and at the LHCb institutes. In addition, we gratefully acknowledge the computing centres and personnel of the Worldwide LHC Computing Grid for delivering so effectively the computing infrastructure essential to our analyses. Finally, we acknowledge the enduring support for the construction and operation of the LHC, the CMS and the LHCb detectors provided by CERN and by many funding agencies. The following agencies provide support for both CMS and LHCb: CAPES, CNPq, FAPERJ and FINEP (Brazil); NSFC (China); CNRS/IN2P3 (France); BMBF, DFG and HGF (Germany); SFI (Ireland); INFN (Italy); NASU (Ukraine); STFC (UK); and NSF (USA). Agencies that provide support for CMS only are BMWFW and FWF (Austria); FNRS and FWO (Belgium); FAPESP (Brazil); MES (Bulgaria); CAS and MoST (China); COLCIENCIAS (Colombia); MSES and CSF (Croatia); RPF (Cyprus); MoER, ERC IUT and ERDF (Estonia); Academy of Finland, MEC, and HIP (Finland); CEA (France); GSRT (Greece); OTKA and NIH (Hungary); DAE and DST (India); IPM (Iran); NRF and WCU (Republic of Korea); LAS (Lithuania); MOE and UM (Malaysia); CINVESTAV, CONACYT, SEP, and UASLP-FAI (Mexico); MBIE (New Zealand); PAEC (Pakistan); MSHE and NSC (Poland); FCT (Portugal); JINR (Dubna); MON, RosAtom, RAS and RFBR (Russia); MESTD (Serbia); SEIDI and CPAN (Spain); Swiss Funding Agencies (Switzerland); MST (Taipei); ThEPCenter, IPST, STAR and NSTDA (Thailand); TUBITAK and TAEK (Turkey); SFFR (Ukraine); and DOE (USA). Agencies that provide support for only LHCb are: FINEP (Brazil); MPG (Germany); FOM and NWO (The Netherlands); MNiSW and NCN (Poland); MEN/IFA (Romania); MinES and FANO (Russia); MinECo (Spain); SNSF and SER (Switzerland). Individuals from the CMS collaboration have received support from the Marie-Curie programme and the European Research Council and EPLANET (European Union); the Leventis Foundation; the A. P. Sloan Foundation; the Alexander von Humboldt Foundation; the Belgian Federal Science Policy Office; the Fonds pour la Formation à la Recherche dans l’Industrie et dans l’Agriculture (FRIABelgium); the Agentschap voor Innovatie door Wetenschap en Technologie (IWT-Belgium); the Ministry of Education, Youth and Sports (MEYS) of the Czech Republic; the Council of Science and Industrial Research, India; the HOMING PLUS programme of Foundation for Polish Science, cofinanced from European Union, Regional Development Fund; the Compagnia di San Paolo (Torino); the Consorzio per la Fisica (Trieste); MIUR project 20108T4XTM (Italy); the Thalis and Aristeia programmes cofinanced by EU-ESF and the Greek NSRF; and the National Priorities Research Program by Qatar National Research Fund. Individual groups or members of the LHCb collaboration have received support from EPLANET, Marie Skłodowska-Curie Actions and ERC (European Union), Conseil général de Haute-Savoie, Labex ENIGMASS and OCEVU, Région Auvergne (France), RFBR (Russia), XuntaGal and GENCAT (Spain), Royal Society and Royal Commission for the Exhibition of 1851 (UK). LHCb is also thankful for the computing resources and the access to software R&D tools provided by Yandex LLC (Russia). The CMS and LHCb collaborations are indebted to the communities behind the multiple open source software packages on which they depend.
Author information
Authors and Affiliations
Consortia
Contributions
All authors have contributed to the publication, being variously involved in the design and the construction of the detectors, in writing software, calibrating sub-systems, operating the detectors and acquiring data and finally analysing the processed data.
Ethics declarations
Competing interests
The author declare no competing financial interests.
Extended data figures and tables
Extended Data Figure 1 Distribution of the dimuon invariant mass in each of the 20 categories.
Superimposed on the data points in black are the combined fit (solid blue) and its components: the Bs0 (yellow shaded) and B0 (light-blue shaded) signal components; the combinatorial background (dash-dotted green); the sum of the semi-leptonic backgrounds (dotted salmon); and the peaking backgrounds (dashed violet). The categories are defined by the range of BDT values for LHCb, and for CMS, by centre-of-mass energy, by the region of the detector in which the muons are detected, and by the range of BDT values. Categories for which both muons are detected in the central region of the CMS detector are denoted with CR, those for which at least one muon was detected into the forward region with FR.
Extended Data Figure 2 Distribution of the dimuon invariant mass for the best six categories.
Categories are ranked according to values of S/(S + B) where S and B are the numbers of signal events expected assuming the SM rates and background events under the Bs0 peak for a given category, respectively. The mass distribution for the six highest-ranking categories, three per experiment, is shown. Superimposed on the data points in black are the combined full fit (solid blue) and its components: the Bs0 (yellow shaded) and B0 (light-blue shaded) signal components; the combinatorial background (dash-dotted green); the sum of the semi-leptonic backgrounds (dotted salmon); and the peaking backgrounds (dashed violet).
Extended Data Figure 3 Schematic of the CMS detector and event display for a candidate Bs0 →μ+μ− decay at CMS.
a, The CMS detector and its components; see ref. 20 for details. b, A candidate Bs0 →μ+μ− decay produced in proton–proton collisions at 8 TeV in 2012 and recorded in the CMS detector. The red arched curves represent the trajectories of the muons from the Bs0 decay candidate.
Extended Data Figure 4 Schematic of the LHCb detector and event display for a candidate Bs0 →μ+μ− decay at LHCb.
a, The LHCb detector and its components; see ref. 21 for details. b, A candidate Bs0 →μ+μ− decay produced in proton–proton collisions at 7 TeV in 2011 and recorded in the LHCb detector. The proton–proton collision occurs on the left-hand side, at the origin of the trajectories depicted with the orange curves. The red curves represent the trajectories of the muons from the Bs0 candidate decay.
Extended Data Figure 5 Confidence level as a function of the B(B0→μ+μ−) hypothesis.
The value of 1 − CL, where CL is the confidence level obtained with the Feldman–Cousins procedure, as a function of B(B0 → µ+µ−) is shown in logarithmic scale. The points mark the computed 1 − CL values and the curve is their spline interpolation. The dark and light (cyan) areas define the two-sided ±1σ and ±2σ confidence intervals for the branching fraction, while the dashed horizontal line defines the confidence level for the 3σ one-sided interval. The dashed (grey) curve shows the 1 − CL values computed from the one-dimensional −2ΔlnL test statistic using Wilks’ theorem. Deviations between these confidence level values and those from the Feldman–Cousins procedure30 illustrate the degree of approximation implied by the asymptotic assumptions inherent to Wilks’ theorem29.
Extended Data Figure 6 Likelihood contours for the ratios of the branching fractions with respect to their SM prediction, in the  versus
versus 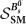 plane.
plane.
a, The (black) cross marks the central value returned by the fit. The SM point is shown as the (red) square located, by construction, at  . Each contour encloses a region approximately corresponding to the reported confidence level. The SM branching fractions are assumed uncorrelated to each other, and their uncertainties are accounted for in the likelihood contours. b, c, Variations of the test statistic −2ΔlnL for
. Each contour encloses a region approximately corresponding to the reported confidence level. The SM branching fractions are assumed uncorrelated to each other, and their uncertainties are accounted for in the likelihood contours. b, c, Variations of the test statistic −2ΔlnL for  and
and  are shown in b and c, respectively. The SM is represented by the (red) vertical lines. The dark and light (cyan) areas define the ±1σ and ±2σ confidence intervals, respectively.
are shown in b and c, respectively. The SM is represented by the (red) vertical lines. The dark and light (cyan) areas define the ±1σ and ±2σ confidence intervals, respectively.
Extended Data Figure 7 Search for the Bs0 →μ+μ− and B0→μ+μ−decays, reported by 11 experiments spanning more than three decades, and by the present results.
Markers without error bars denote upper limits on the branching fractions at 90% confidence level, while measurements are denoted with error bars delimiting 68% confidence intervals. The solid horizontal lines represent the SM predictions for the Bs0 and B0 → µ+µ− branching fractions1; the blue (red) lines and markers relate to the Bs0 (B0 → µ+µ−) decay. Data (see key) are from refs 17, 18, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60; for details see Methods. Inset, magnified view of the last period in time.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported licence. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons licence, users will need to obtain permission from the licence holder to reproduce the material. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-sa/3.0/.
About this article
Cite this article
CMS Collaboration., LHCb Collaboration. Observation of the rare Bs0 →µ+µ− decay from the combined analysis of CMS and LHCb data. Nature 522, 68–72 (2015). https://doi.org/10.1038/nature14474
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature14474
This article is cited by
-
\( \overline{B}\to \overline{D}D \) decays and the extraction of fd/fu at hadron colliders
Journal of High Energy Physics (2024)
-
Spectroscopic properties of \( B \) and \( B_s \) meson using screened potential
Indian Journal of Physics (2024)
-
Heavy flavour physics and CP violation at LHCb: A ten-year review
Frontiers of Physics (2023)
-
Recent progress in decays of b and c hadrons
Indian Journal of Physics (2023)
-
Electroweak baryogenesis in aligned two Higgs doublet models
Journal of High Energy Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.



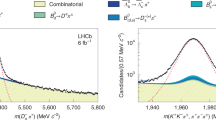




 versus
versus 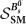 plane.
plane.