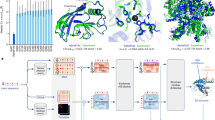
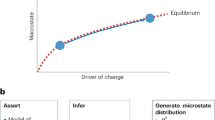
Abstract
Classical crystallography can determine structures as complicated as multi-component ribosomal assemblies with atomic resolution, but is inadequate for disordered systems—even those as simple as water ice—that occupy the complex middle ground between liquid-like randomness and crystalline periodic order. Correlated disorder nevertheless has clear crystallographic signatures that map to the type of disorder, irrespective of the underlying physical or chemical interactions and material involved. This mapping hints at a common language for disordered states that will help us to understand, control and exploit the disorder responsible for many interesting physical properties.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Kuhs, W. F. & Lehmann, M. S. The structure of ice-Ih. Water Sci. Rev. 2, 1–66 (1986).
Cartwright, J. H. E. & Mackay, A. L. Beyond crystals: the dialectic of materials and information. Phil. Trans. R. Soc. Lond. A 370, 2807–2822 (2012).
Bernal, J. D. & Carlisle, C. H. The range of generalised crystallography. Sov. Phys. Crystallogr. 13, 811–831 (1969).
Damasceno, P. F., Engel, M. & Glotzer, S. C. Predictive self-assembly of polyhedra into complex structures. Science 337, 453–457 (2012).
Lonsdale, K. & Smith, H. An experimental study of diffuse X-ray reflexion by single crystals. Proc. R. Soc. A 179, 8–50 (1941).
Lonsdale, K. X-ray study of crystal dynamics: an historical and critical survey of experiment and theory. Proc. Phys. Soc. 54, 314–353 (1942).
Maisel, S. B., Schindzielorz, N., Müller, S., Reichert, H. & Bosak, A. An accidental visualization of the Brillouin zone in an Ni-W alloy via diffuse scattering. J. Appl. Cryst. 46, 1211–1215 (2013).
Welberry, T. R., Heerdegen, A. P., Goldstone, D. C. & Taylor, I. A. Diffuse scattering resulting from macromolecular frustration. Acta Crystallogr. B 67, 516–524 (2011).This elegantly describes how a complicated diffuse scattering pattern might be explained in terms of simple disordering rules.
Welberry, T. R. et al. Diffuse neutron scattering in benzil, C14D10O2, using the time-of-flight Laue technique. J. Appl. Cryst. 36, 1440–1447 (2003).
Keen, D. A., Gutmann, M. J. & Wilson, C. C. SXD—the single crystal diffractometer at the ISIS Spallation Neutron Source. J. Appl. Cryst. 39, 714–722 (2006).
Withers, R. L. Disorder, structured diffuse scattering and the transmission electron microscope. Z. Kristallogr. 220, 1027–1034 (2005).
Soper, A. K. & Barney, E. R. Extracting the pair distribution function (PDF) from white beam X-ray total scattering data. J. Appl. Cryst. 44, 714–726 (2011).
Keen, D. A. A comparison of various commonly used correlation functions for describing total scattering. J. Appl. Cryst. 34, 172–177 (2001).
Chupas, P. J. et al. Rapid-acquisition pair distribution function (RA-PDF) analysis. J. Appl. Cryst. 36, 1342–1347 (2003).
Skinner, L. B., Benmore, C. J. & Parise, J. B. Area detector corrections for high quality synchrotron X-ray structure factor measurements Nucl. Instrum. Meth. A 662, 61–70 (2012).
Bennett, T. D. et al. Structure and properties of an amorphous metal-organic framework. Phys. Rev. Lett. 104, 115503 (2010).
Farrow, C. L. et al. PDFfit2 and PDFgui: computer programs for studying nanostructure in crystals. J. Phys. Condens. Matter 19, 335219 (2007).
Butler, B. D. & Welberry, T. R. Calculation of diffuse scattering from simulated disordered crystals: a comparison with optical transforms. J. Appl. Cryst. 25, 391–399 (1992).
Neder, R. B. & Proffen, T. Diffuse Scattering and Defect Structure Simulations: A Cook Book using the Program DISCUS (Oxford Univ. Press, 2008).
Goossens, D. J., Heerdegen, A. P., Chan, E. J. & Welberry, T. R. Monte Carlo modeling of diffuse scattering from single crystals: the program ZMC. Metall. Mater. Trans. A 42, 23–31 (2011).
Welberry, T. R., Chan, E. J., Goossens, D. J. & Heerdegen, A. P. Use of Monte Carlo simulation for the interpretation and analysis of diffuse scattering. Phase Transit. 83, 80–98 (2010).
Chan, E. J. et al. Single-crystal diffuse scattering studies on polymorphs of molecular crystals. I. The room-temperature polymorphs of the drug benzocaine. Acta Crystallogr. B 65, 382–392 (2009).
Welberry, T. R. & Paściak, M. Monte Carlo and molecular dynamics simulation of disorder in the Ag+ fast ion conductors pearceite and polybasite. Metall. Mater. Trans. A 42, 6–13 (2011).
Eggeman, A. S., Illig, S., Troisi, A., Sirringhaus, H. & Midgley, P. A. Measurement of molecular motion in organic semiconductors by thermal diffuse electron scattering. Nature Mater. 12, 1045–1049 (2013).
Xu, R. & Chiang, T. C. Determination of phonon dispersion relations by X-ray thermal diffuse scattering. Z. Kristallogr. 220, 1009–1016 (2005).
Gutmann, M. J. et al. Room temperature single-crystal diffuse scattering and ab initio lattice dynamics in CaTiSiO5 . J. Phys. Condens. Matter 25, 315402 (2013).
Paddison, J. A. M. et al. Emergent frustration in Co-doped β-Mn. Phys. Rev. Lett. 110, 267207 (2013).Reverse Monte Carlo analysis of an experiment uncovers an unexpected magnetic structure with a simple underlying basis.
McGreevy, R. L. Reverse Monte Carlo modelling. J. Phys. Condens. Matter 13, R877–R913 (2001).
Tucker, M. G., Keen, D. A., Dove, M. T., Goodwin, A. L. & Hui, Q. RMCProfile: reverse Monte Carlo for polycrystalline materials. J. Phys. Condens. Matter 19, 335218 (2007).
Wannier, G. H. Antiferromagnetism. The triangular Ising net. Phys. Rev. 79, 357–364 (1950).
Paddison, J. A. M., Stewart, J. R. & Goodwin, A. L. SPINVERT: a program for refinement of paramagnetic diffuse scattering data. J. Phys. Condens. Matter 25, 454220 (2013).
Nakatsuji, S. et al. Spin-orbital short-range order on a honeycomb-based lattice. Science 336, 559–563 (2012).
Rasche, B. et al. Stacked topological insulator built from bismuth-based graphene sheet analogues. Nature Mater. 12, 422–425 (2013).
Paddison, J. A. M. et al. Spin correlations in Ca3Co2O6: polarized-neutron diffraction and Monte Carlo study. Phys. Rev. B 90, 014411 (2014).
Lacroix, C., Mendels, P. & Mila, F. Introduction to Frustrated Magnetism: Materials, Experiments, Theory (Springer, 2011).
Lynn, J. W. et al. Order and dynamics of intrinsic nanoscale inhomogeneities in manganites. Phys. Rev. B 76, 014437 (2007).
Shintani, H. & Tanaka, H. Frustration on the way to crystallization in glass. Nature Phys. 2, 200–206 (2006).
Wood, B. C. & Marzari, N. Dynamical structure and thermodynamics of the superionic sublattice in α-AgI. Phys. Rev. Lett. 97, 166401 (2006).
Ogitsu, T., Schwegler, E. & Galli, G. β-rhombohedral boron: at the crossroads of the chemistry of boron and the physics of frustration. Chem. Rev. 113, 3425–3449 (2013).
Pauling, L. The structure and entropy of ice and of other crystals with some randomness of atomic arrangement. J. Am. Chem. Soc. 57, 2680–2684 (1935).
Fairbank, V. E., Thompson, A. L., Cooper, R. I. & Goodwin, A. L. Charge-ice dynamics in the negative thermal expansion material Cd(CN)2 . Phys. Rev. B 86, 104113 (2012).
Bramwell, S. T. et al. Spin correlations in Ho2Ti2O7: a dipolar spin ice system. Phys. Rev. Lett. 87, 047205 (2001).One of the first experimental papers that initiated the studies of spin ices and subsequent searches for magnetic monopoles.
Fennell, T. et al. Magnetoelastic excitations in the pyrochlore spin liquid Tb2Ti2O7 . Phys. Rev. Lett. 112, 017203 (2014).
Madden, P. A., O'Sullivan, K. F. & Chiarotti, G. Ordering of the silver ions in α-AgI: a mechanism for the α-β phase transition. Phys. Rev. B 45, 10206–10212 (1992).
Tucker, M. T., Squires, M. P., Dove, M. T. & Keen, D. A. Dynamic structural disorder in cristobalite: neutron total scattering measurement and reverse Monte Carlo modelling. J. Phys. Condens. Matter 13, 403–423 (2001).
Levin, I., Krayzman, V. & Woicik, J. C. Local structure in perovskite (Ba,Sr)TiO3: Reverse Monte Carlo refinements from multiple measurement techniques. Phys. Rev. B 89, 024106 (2014).
Comès, R., Lambert, M. & Guinier, A. Désordre linéaire dans les cristaux (cas du silicium, du quartz, et des pérovskites ferroélectriques). Acta Crystallogr. A 26, 244–254 (1970).
Božin, E. S. et al. Entropically stabilized local dipole formation in lead chalcogenides. Science 330, 1660–1663 (2010).
Hull, S. et al. Neutron total scattering study of the delta and beta phases of Bi2O3 . Dalton Trans. 2009, 8737–8745 (2009).
Keeble, D. S. et al. Bifurcated polarization rotation in bismuth-based piezoelectrics. Adv. Funct. Mater. 23, 185–190 (2013).‘Big-box’ modelling of total scattering shows how the local polarization changes within a higher-symmetry average lattice.
Zhang, W., Cai, Y., Xiong, R.-G., Yoshikawa, H. & Awaga, K. Exceptional dielectric phase transitions in a perovskite-type cage compound. Angew. Chem. Int. Ed. 49, 6608–6610 (2010).
Berret, J.-F., Bostoen, C. & Hennion, B. Phase diagram of the dipolar glass K1−x(NH4)xI. Phys. Rev. B 46, 13747–13750 (1992).
David, W. I. F., Ibberson, R. M., Dennis, T. J. S., Hare, J. P. & Prassides, K. Structural phase transitions in the fullerene C60 . Europhys. Lett. 18, 219–225 (1992).
Liu, X. et al. Structural changes in a marine podovirus associated with release of its genome into Prochlorococcus. Nature Struct. Mol. Biol. 17, 830–836 (2010).
Xu, G., Wen, J., Stock, C. & Gehring, P. M. Phase instability induced by polar nanoregions in a relaxor ferroelectric system. Nature Mater. 7, 562–566 (2008).
Billinge, S. J. L., Proffen, Petkov, V., Sarrao, J. L. & Kycia, S. Evidence for charge localization in the ferromagnetic phase of La1−xCaxMnO3 from high real-space-resolution x-ray diffraction. Phys. Rev. B 62, 1203–1211 (2000).
Bennemann, K. H., Ketterson, J. B., eds. Superconductivity: Conventional and Unconventional Superconductors Vol. 1 (Springer, 2008).
Mühlbauer, S. et al. Skyrmion lattice in a chiral magnet. Science 323, 915–919 (2009).
Bramwell, S. T. et al. Measurement of the charge and current of magnetic monopoles in spin ice. Nature 461, 956–959 (2009).
Christensen, M. et al. Avoided crossing of rattler modes in thermoelectric materials. Nature Mater. 7, 811–815 (2008).
Bowron, D. T. et al. NIMROD: The Near and InterMediate Range Order Diffractometer of the ISIS second target station. Rev. Sci. Instrum. 81, 033905 (2010).
Cliffe, M. J. et al. Correlated defect nanoregions in a metal–organic framework. Nature Commun. 5, 4176 (2014).
Rademacher, N., Daemen, L. L., Chronister, E. L. & Proffen, T. Pair distribution function analysis of molecular compounds: significance and modeling approach discussed using the example of p-terphenyl. J. Appl. Cryst. 45, 482–488 (2012).
Goossens, D. J. & Whitfield, R. E. Distinguishing types of disorder in diffuse scattering: a numerical simulation study. Metall. Mater. Trans. A 45, 152–161 (2014).
Krayzman, V. & Levin, I. Reverse Monte Carlo refinements of nanoscale atomic correlations using powder and single-crystal diffraction data. J. Appl. Cryst. 45, 106–112 (2012).
Weber, T. & Simonov, A. The three-dimensional pair distribution function analysis of disordered single crystals: basic concepts. Z. Kristallogr. 227, 238–247 (2012).
Danilkin, S. A. Diffuse scattering and lattice dynamics of superionic copper chalcogenides. Solid State Ionics 180, 483–487 (2009).
Chang, L.-J. et al. Higgs transition from a magnetic Coulomb liquid to a ferromagnet in Yb2Ti2O7 . Nature Commun. 3, 992 (2012).
Wehinger, B. et al. Diffuse scattering in Ih ice. J. Phys. Condens. Matter 26, 265401 (2014).High-quality X-ray diffuse and inelastic scattering and computer simulations are combined to show how the molecules in water ice disorder.
Kwei, G. H., Lawson, A. C., Billinge, S. J. L. & Cheong, S.-W. Structures of the ferroelectric phases of barium titanate. J. Phys. Chem. 97, 2368–2377 (1993).
Algara-Siller, G. et al. Square ice in graphene nanocapillaries. Nature 519, 443–445 (2015).
Bernal, J. D. & Fowler, R. H. A theory of water and ionic solution, with particular reference to hydrogen and hydroxyl ions. J. Chem. Phys. 1, 515–548 (1933).
Lieb, E. H. Residual entropy of square ice. Phys. Rev. 162, 162–172 (1967).
Acknowledgements
We are grateful for discussions with J. A. M. Paddison, M. J. Cliffe and A. B. Cairns. A.L.G. acknowledges financial support from the ERC (grant number 279705).
Author information
Authors and Affiliations
Contributions
D.A.K. and A.L.G. contributed equally to this work.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Keen, D., Goodwin, A. The crystallography of correlated disorder. Nature 521, 303–309 (2015). https://doi.org/10.1038/nature14453
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature14453
This article is cited by
-
Tuning electronic and phononic states with hidden order in disordered crystals
Nature Communications (2023)
-
Quantitative three-dimensional local order analysis of nanomaterials through electron diffraction
Nature Communications (2023)
-
Hidden chemical order in disordered Ba7Nb4MoO20 revealed by resonant X-ray diffraction and solid-state NMR
Nature Communications (2023)
-
Machine learning in scanning transmission electron microscopy
Nature Reviews Methods Primers (2022)
-
From atomically resolved imaging to generative and causal models
Nature Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.