Abstract
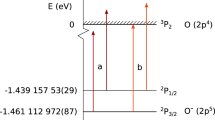
The chemical properties of an element are primarily governed by the configuration of electrons in the valence shell. Relativistic effects influence the electronic structure of heavy elements in the sixth row of the periodic table, and these effects increase dramatically in the seventh row—including the actinides—even affecting ground-state configurations1,2. Atomic s and p1/2 orbitals are stabilized by relativistic effects, whereas p3/2, d and f orbitals are destabilized, so that ground-state configurations of heavy elements may differ from those of lighter elements in the same group. The first ionization potential (IP1) is a measure of the energy required to remove one valence electron from a neutral atom, and is an atomic property that reflects the outermost electronic configuration. Precise and accurate experimental determination of IP1 gives information on the binding energy of valence electrons, and also, therefore, on the degree of relativistic stabilization. However, such measurements are hampered by the difficulty in obtaining the heaviest elements on scales of more than one atom at a time3,4,5. Here we report that the experimentally obtained IP1 of the heaviest actinide, lawrencium (Lr, atomic number 103), is  electronvolts. The IP1 of Lr was measured with 256Lr (half-life 27 seconds) using an efficient surface ion-source and a radioisotope detection system coupled to a mass separator. The measured IP1 is in excellent agreement with the value of 4.963(15) electronvolts predicted here by state-of-the-art relativistic calculations. The present work provides a reliable benchmark for theoretical calculations and also opens the way for IP1 measurements of superheavy elements (that is, transactinides) on an atom-at-a-time scale.
electronvolts. The IP1 of Lr was measured with 256Lr (half-life 27 seconds) using an efficient surface ion-source and a radioisotope detection system coupled to a mass separator. The measured IP1 is in excellent agreement with the value of 4.963(15) electronvolts predicted here by state-of-the-art relativistic calculations. The present work provides a reliable benchmark for theoretical calculations and also opens the way for IP1 measurements of superheavy elements (that is, transactinides) on an atom-at-a-time scale.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout


Similar content being viewed by others
References
Pyykkö, P. Relativistic effects in structural chemistry. Chem. Rev. 88, 563–594 (1988)
Pershina, V. in Relativistic Methods for Chemists (eds Barysz, M. & Ishikawa, Y.) 451–520 (Challenges and Advances in Computational Chemistry and Physics 10, Springer, 2010)
Oganessian Heaviest nuclei from 48Ca-induced reactions. J. Phys. G 34, R165–R242 (2007)
Schädel M., Shaughnessy D., eds. The Chemistry of Superheavy Elements 2nd edn (Springer, 2014)
Türler, A. & Pershina, V. Advances in the production and chemistry of the heaviest elements. Chem. Rev. 113, 1237–1312 (2013)
Schädel, M. et al. Chemical properties of element 106 (seaborgium). Nature 388, 55–57 (1997)
Eichler, R. et al. Chemical characterization of bohrium (element 107). Nature 407, 63–65 (2000)
Düllmann, E. et al. Chemical investigation of hassium (element 108). Nature 418, 859–862 (2002)
Eichler, R. et al. Chemical characterization of element 112. Nature 447, 72–75 (2007)
Even, J. et al. Synthesis and detection of a seaborgium carbonyl complex. Science 345, 1491–1493 (2014)
Köhler, S. et al. First experimental determination of the ionization potentials of berkelium and californium. Angew. Chem. Int. Edn Engl. 35, 2856–2858 (1996)
Peterson, J. et al. Determination of the first ionization potential of einsteinium by resonance ionization mass spectroscopy (RIMS). J. Alloy. Comp. 271–273, 876–878 (1998)
Sewtz, M. et al. First observation of atomic levels for the element fermium (Z = 100). Phys. Rev. Lett. 90, 163002 (2003)
Rothe, S. et al. Measurement of the first ionization potential of astatine by laser ionization spectroscopy. Nature Commun. 4, 1835 (2013)
Desclaux, J.-P. & Fricke, B. Relativistic prediction of the ground state of atomic lawrencium. J. Phys. 41, 943–946 (1980)
Eliav, E., Kaldor, U. & Ishikawa, Y. Transition energies of ytterbium, lutetium, and lawrencium by the relativistic coupled-cluster method. Phys. Rev. A 52, 291–296 (1995)
Zou, Y. & Fischer, C. F. Resonance transition energies and oscillator strengths in lutetium and lawrencium. Phys. Rev. Lett. 88, 183001 (2002)
Borschevsky, A. et al. Transition energies of atomic lawrencium. Eur. Phys. J. D 45, 115–119 (2007)
Dzuba, V. A., Safronova, M. S. & Safronova, U. I. Atomic properties of superheavy elements No, Lr, and Rf. Phys. Rev. A 90, 012504 (2014)
Sato, T. K. et al. First successful ionization of Lr (Z = 103) by a surface-ionization technique. Rev. Sci. Instrum. 84, 023304(5) (2013)
Stora, T. Radioactive Ion Sources. CERN-2013-007, 331–349 http://cds.cern.ch/record/1693046 (accessed, November 2014)
Zandberg, É. Y. & Ionov, N. I. Surface ionization. Sov. Phys. Usp. 2, 255–281 (1959)
Kirchner, R. On the thermoionization in hot cavities. Nucl. Instrum. Methods A 292, 203–208 (1990)
Kramida, A., Ralchenko, Y., Reader, J. & Team, N. A. NIST Atomic Spectra Database version 5.1 (2013); http://physics.nist.gov/asd (accessed, July 2014)
Shabaev, V. M., Tupitsyn, I. I. & Yerokhin, V. A. QEDMOD: Fortran program for calculating the model Lamb-shift operator. Comput. Phys. Commun. 189, 175–181 (2015)
Maeda, H., Mizugai, Y., Matsumoto, Y., Suzuki, A. & Takami, M. Highly excited even Rydberg series of Lu I studied by two-step laser photoionization spectroscopy. J. Phys. B 22, L511–L516 (1989)
Liu, W., Küchle, W. & Dolg, M. Ab initio pseudopotential and density-functional all-electron study of ionization and excitation energies of actinide atoms. Phys. Rev. A 58, 1103–1110 (1998)
Cao, X., Dolg, M. & Stoll, H. Valence basis sets for relativistic energy-consistent small-core actinide pseudopotentials. J. Chem. Phys. 118, 487–496 (2003)
Sato, N. et al. Production of 256Lr in the 249,250,251Cf + 11B, 243Am + 18O, and 248Cm + 14N reactions. Radiochim. Acta 102, 211–219 (2014)
Sato, T. K. et al. Development of a He/CdI2 gas-jet system coupled to a surface-ionization type ion-source in JAEA-ISOL: towards determination of the first ionization potential of Lr (Z = 103). J. Radioanal. Nucl. Chem. 303, 1253–1257 (2015)
Visscher, L. et al. DIRAC, a relativistic ab initio electronic structure program. Release DIRAC13 http://www.diracprogram.org (2013)
Faegri, K. Relativistic Gaussian basis sets for the elements K-Uuo. Theor. Chem. Acc. 105, 252–258 (2001)
Visscher, L. & Dyall, K. G. Dirac–Fock atomic electronic structure calculations using different nuclear charge distributions. At. Data Nucl. Data Tables 67, 207–224 (1997)
Eliav, E., Kaldor, U. & Ishikawa, Y. Open-shell relativistic coupled-cluster method with Dirac-Fock-Breit wave functions: energies of the gold atom and its cation. Phys. Rev. A 49, 1724–1729 (1994)
Acknowledgements
We thank the JAEA tandem accelerator crew for supplying intense and stable beams for the experiments. The 249Cf was made available by H. Nitsche (Univ. California, Berkeley); it was produced in the form of 249Bk through the former Transplutonium Element Production Program at Oak Ridge National Laboratory (ORNL) under the auspices of the Director, Office of Science, Office of Basic Energy Sciences, Chemical Sciences, Geosciences, and Biosciences Division of the US Department of Energy. Financial support by the Helmholtz-Institut Mainz is acknowledged. This work has been partly supported by the Grant-in-Aid for Scientific Research (C) no. 26390119 of the Ministry of Education, Science, Sports and Culture (MEXT).
Author information
Authors and Affiliations
Contributions
T.K.S., M.A., Y.N. and M.S. prepared the main part of the manuscript, A.B., E. E. and U.K. contributed to the theory part, and T.S. to the experimental part. C.E.D. and J.V.K. commented on the manuscript. T.K.S, M.A., T.S., N.S., K.T. and S.I. developed the surface ion-source in the ISOL setup at the JAEA tandem accelerator facility. T.K.S. and M.A. were responsible for data acquisition and analysis. T.S. commented on ion-source optimizations and the data analysis procedure. K.T. prepared the 249Cf target. K.E., J.R., P.T.-P., C.E.D. and N.T. separated and provided the 249Cf for the target. The on-line experiments were performed by T.K.S., M.A., N.S., Y.K., K.T., S. I., S.M., Y.N., K.O., A.O., D.R., M.S. and A.T., while theoretical calculations were carried out by A.B., E.E. and U.K. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
PowerPoint slides
Source data
Rights and permissions
About this article
Cite this article
Sato, T., Asai, M., Borschevsky, A. et al. Measurement of the first ionization potential of lawrencium, element 103. Nature 520, 209–211 (2015). https://doi.org/10.1038/nature14342
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature14342
This article is cited by
-
Recent progress in experiments on the heaviest nuclides at SHIP
La Rivista del Nuovo Cimento (2022)
-
Filament studies for laser spectroscopy on lawrencium
Hyperfine Interactions (2020)
-
The Periodic Table
Journal of Astrophysics and Astronomy (2020)
-
Scaling of the Mutual Screening Parameter of the Charge of the Nucleus for Valence ns2-Electrons in Atoms of Intermediate and Heavy Elements
Russian Physics Journal (2020)
-
Extreme chemistry: experiments at the edge of the periodic table
Nature (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.