Abstract
Nearly a century ago it was recognized1 that radiation absorption by stellar matter controls the internal temperature profiles within stars. Laboratory opacity measurements, however, have never been performed at stellar interior conditions, introducing uncertainties in stellar models2,3,4,5. A particular problem arose2,3,6,7,8 when refined photosphere spectral analysis9,10 led to reductions of 30–50 per cent in the inferred amounts of carbon, nitrogen and oxygen in the Sun. Standard solar models11 using the revised element abundances disagree with helioseismic observations that determine the internal solar structure using acoustic oscillations. This could be resolved if the true mean opacity for the solar interior matter were roughly 15 per cent higher than predicted2,3,6,7,8, because increased opacity compensates for the decreased element abundances. Iron accounts for a quarter of the total opacity2,12 at the solar radiation/convection zone boundary. Here we report measurements of wavelength-resolved iron opacity at electron temperatures of 1.9–2.3 million kelvin and electron densities of (0.7–4.0) × 1022 per cubic centimetre, conditions very similar to those in the solar region that affects the discrepancy the most: the radiation/convection zone boundary. The measured wavelength-dependent opacity is 30–400 per cent higher than predicted. This represents roughly half the change in the mean opacity needed to resolve the solar discrepancy, even though iron is only one of many elements that contribute to opacity.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Eddington, A. S. The Internal Constitution of the Stars (Cambridge Univ. Press, 1926)
Basu, S. & Antia, H. M. Helioseismology and solar abundances. Phys. Rep. 457, 217–283 (2008)
Basu, S., Grevesse, N., Mathis, S. & Turck-Chièze, S. Understanding the internal chemical composition and physical processes of the solar interior. Space Sci. Rev. http://dx.doi.org/10.1007/s11214-014-0035-9 (2014)
Christensen-Dalsgaard, J. in Proc. IAU Symp. No. 258, The Ages of Stars (2008) (eds Mamajek, E. E., Soderblom, D. R. & Wyse, R. F. G. ) 431–442 (International Astronomical Union, 2009)
Delahaye, F. & Pinsonneault, M. Comparison of radiative accelerations obtained with atomic data from OP and OPAL. Astrophys. J. 625, 563–574 (2005)
Bahcall, J. N., Serenelli, A. M. & Pinsonneault, M. How accurately can we calculate the depth of the solar convective zone? Astrophys. J. 614, 464–471 (2004)
Turck-Chièze, S. et al. Surprising Sun: a new step towards a complete picture? Phys. Rev. Lett. 93, 211102 (2004)
Serenelli, A. M., Basu, S., Ferguson, J. W. & Asplund, M. New solar composition: the problem with solar models revisited. Astrophys. J. 705, L123–L127 (2009)
Asplund, M., Grevesse, N., Sauval, J. A. & Scott, P. The chemical composition of the Sun. Annu. Rev. Astron. Astrophys. 47, 481–522 (2009)
Caffau, E. et al. Solar chemical abundances determined with a CO5BOLD 3D model atmosphere. Sol. Phys. 268, 255–269 (2011)
Bahcall, J. N. et al. Standard solar models and the uncertainties in predicted capture rates of solar neutrinos. Rev. Mod. Phys. 54, 767–799 (1982)
Blancard, C., Cosse & Faussurier, G. Solar mixture opacity calculations using detailed configuration and level accounting treatments. Astrophys. J. 745, 10 (2012)
Nahar, S. N., Pradhan, A. K., Chen, G.-X. & Eissner, W. Highly excited core resonances in photoionization of Fe XVII: implications for plasma opacities. Phys. Rev. A 83, 053417 (2011)
Rosseland, S. Note on the absorption of radiation within a star. Mon. Not. R. Astron. Soc. 84, 525–528 (1924)
Perry, T. S. et al. Absorption experiments on x-ray-heated mid-Z constrained samples. Phys. Rev. E 54, 5617–5631 (1996)
Bailey, J. E. et al. Experimental investigation of opacity models for stellar interior, inertial fusion, and high energy density plasmas. Phys. Plasmas 16, 058101 (2009)
Bailey, J. E. et al. Iron-plasma transmission measurements at temperatures above 150 eV. Phys. Rev. Lett. 99, 265002 (2007)
Rochau, G. A. et al. ZAPP: the Z Astrophysical Plasma Properties collaboration. Phys. Plasmas 21, 056308 (2014)
Davidson, S. J. et al. Investigation of the opacity of hot, dense aluminum in the region of its K edge. Appl. Phys. Lett. 52, 847–849 (1988)
Foster, J. M. et al. L-shell absorption spectrum of an open-M-shell germanium plasma: comparison of experimental data with a detailed configuration-accounting calculation. Phys. Rev. Lett. 67, 3255–3258 (1991)
Nash, T. J., Rochau, G. A. & Bailey, J. E. Design of dynamic Hohlraum opacity samples to increase measured sample density on Z. Rev. Sci. Instrum. 81, 10E518 (2010)
Nagayama, T. et al. Control and diagnosis of temperature, density, and uniformity in x-ray heated iron/magnesium samples for opacity measurements. Phys. Plasmas 21, 056502 (2014)
Hansen, S., Bauche, J., Bauche-Arnoult, C. & Gu, M. Hybrid atomic models for spectroscopic plasma diagnostics. High Energy Density Phys. 3, 109–114 (2007)
Iglesias, C. A. & Rogers, F. J. Opacities for the solar radiative interior. Astrophys. J. 371, 408–417 (1991)
Seaton, M. J., Yu, Y., Mihalas, D. & Pradhan, A. K. Opacities for stellar envelopes. Mon. Not. R. Astron. Soc. 266, 805–828 (1994)
Badnell, N. R. et al. Updated opacities from the opacity project. Mon. Not. R. Astron. Soc. 360, 458–464 (2005)
Colgan, J. et al. Light element opacities from ATOMIC. High Energy Density Phys. 9, 369–374 (2013)
Porcherot, Q., Pain, J.-C., Gilleron, F. & Blenski, T. A consistent approach for mixed detailed and statistical calculation of opacities in hot plasmas. High Energy Density Phys. 7, 234–239 (2011)
Bailey, J. E. et al. Dynamic hohlraum radiation hydrodynamics. Phys. Plasmas 13, 056301 (2006)
Bailey, J. E. et al. Diagnosis of x-ray heated Mg/Fe opacity research plasmas. Rev. Sci. Instrum. 79, 113104 (2008)
Jeynes, C., Barradas, N. P. & Szilágyi, E. Accurate determination of quantity of material in thin films by Rutherford backscattering spectrometery. Anal. Chem. 84, 6061–6069 (2012)
Loisel, G. et al. A methodology for calibrating wavelength dependent spectral resolution for crystal spectrometers. Rev. Sci. Instrum. 83, 10E133 (2012)
Henke, B. L. et al. Low-energy x-ray response of photographic films. II. Experimental characterization. J. Opt. Soc. Am. B 1, 828–849 (1984)
Nagayama, T. et al. Parallax diagnostics of radiation source geometric dilution for iron opacity experiments. Rev. Sci. Instrum. 85, 11D603 (2014)
MacFarlane, J. J. et al. in Proc. Int. Symp. on Inertial Fusion Science and Applications (Monterey, California, 2003) 457–464 (American Nuclear Society, 2003)
Henke, B. L., Gullikson, G. M. & Davis, J. C. X-ray interactions: photoabsorption, scattering, transmission, and reflection at E = 50-30,000 eV, Z = 1-92. At. Data Nucl. Data Tables 54, 181–342 (1993)
del Grande, N. K. L Shell photoabsorption spectroscopy for solid metals: Ti, V, Cr, Fe, Ni, Cu. Phys. Scr. 41, 110–114 (1990)
Zheng, L., Cui, M.-Q., Zhu, J. & Zhao, Y.-D. Determination of the photoabsorption cross-sections of Al and Fe films in the soft x-ray region using synchrotron radiation. High Energy Phys. Nuclear Phys. 28, 1121–1125 (2004)
Cowan, R. D. The Theory of Atomic Structure and Spectra (Univ. California Press, 1981)
MacFarlane, J. J., Golovkin, I. E. & Woodruff, P. R. HELIOS-CR—a 1-D radiation-magnetohydrodynamics code with inline atomic kinetics modeling. J. Quant. Spectrosc. Radiat. Transf. 99, 381–397 (2006)
Nagayama, T. et al. Investigation of iron opacity experiment plasma gradients with synthetic data analyses. Rev. Sci. Instrum. 83, 10E128 (2012)
Acknowledgements
Sandia is a multiprogramme laboratory operated by Sandia Corporation, a Lockheed Martin Company, for the United States Department of Energy under contract DE-AC04-94AL85000. The Los Alamos National Laboratory is operated by Los Alamos National Security, LLC, for the NNSA of the US DOE under contract number DE-AC5206NA25396. J.E.B. acknowledges support from a DOE High Energy Density Laboratory Plasmas grant. A.K.P. and C.O. also acknowledge support from a DOE High Energy Density Laboratory Plasmas grant. We appreciate the efforts of the entire Z facility team. We thank S. Turck-Chièze, H. Morris, and M. Pinsonneault for discussions. We also thank R. W. Lee for critiquing the manuscript. We appreciate support for the experiments provided by R. J. Leeper, J. L. Porter, M. K. Matzen and M. Herrmann.
Author information
Authors and Affiliations
Contributions
These measurements were conceived and planned by J.E.B. and G.A.R. J.E.B. was the primary author of the manuscript, with important contributions from T.N. Experiments were conducted by J.E.B., G.A.R. and G.P.L. The Z-facility data were analysed by T.N., J.E.B. and G.P.L., with assistance from G.A.R., C.A.I., B.G.W., I.G., J.J. M. and R.C.M. OPAS calculations were performed by C.B., G.F. and Ph.C. ATOMIC calculations were performed by J.C., with assistance from C.F., D.P.K. and M.S. SCRAM calculations were provided by S.B.H. SCO calculations were performed by J.-C.P. and F.G. OP calculations were performed by C.O., with assistance from A.K.P. and S.N.N. All authors discussed the results, commented on the manuscript, and contributed to the interpretation.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
Extended Data Figure 1 Schematic diagram of four sample configurations used in Z opacity experiments.
The FeMg layer (red line) is completely encapsulated by the CH (blue) in order to avoid exposure to atmosphere during the experiment preparation. One sample type employed a Be tamper (yellow) to provide additional tamping while greatly reducing both the attenuation and emission in comparison with CH. Te and ne both increase as the tamper mass increases. The tamper thicknesses and the resulting average Te and ne values22 are listed below each sample type. Experiments were also conducted using the same tamper construction, but without the FeMg layer, to provide calibrations of the opacity measurement accuracy.
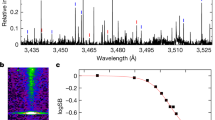
Extended Data Figure 2 Data illustrating the transmission determination method.
The five experiments shown here were conducted with a CH + Be tamper. a, The seven measurements of the unattenuated spectral intensity I from five experiments using the CCP4a and CCP10a spectrometers are denoted with black lines. The mean spectral intensity <I> (red) is used to determine transmission, [σ/I]abs represents the absolute percentage unattenuated spectrum 1σ uncertainty (green), and [σ/I]rel represents the relative percentage 1σ uncertainty as a function of wavelength (blue). A similar collection of data are obtained from the seven CCP4b and CCP10b spectrometer measurements. (arb, arbitrary units.) b, The attenuated (red) and unattenuated (blue) spectral intensities used to determine the transmission on experiment Z2624. These data were recorded with the CCP4a and CCP10a crystals and a similar data set (not shown) was recorded with the CCP4b and CCP10b crystals. c, The transmissions T measured on Z2624 agree within the 1σ uncertainties. d, The optical depth (τ, red) inferred by taking the natural log of the mean transmission measured on Z2624 includes contributions from both Fe and Mg. The optical depth corresponding to the iron contribution only (black) is inferred by subtracting the Mg contribution calculated with PrismSPECT35 (blue) from the FeMg mixture measurement. e, The mean opacities κ inferred from the three Be-tamped iron opacity measurements (solid), along with 1σ fractional absolute uncertainties (dashed). f, These measurements are combined to infer the overall mean opacity (<κ>, red) and associated 1σ fractional uncertainty (blue) for these conditions. The error bars in b, c, and e represent the 1σ uncertainty.
Extended Data Figure 3 The measured Z iron opacity exceeds the room-temperature value for wavelengths where models predict the opacity is dominated by photoionization.
a, The measured iron opacity from the Be-tamped result is larger than the room-temperature value36,37 for wavelengths shorter than approximately 9 Å. The error bars correspond to 1σ uncertainties. b, The SCRAM opacity model predicts that the ratio of the bound–free (BF) opacity contribution with the total opacity (blue) is larger than the ratio of the bound–bound (BB) opacity contribution with the total (red) for wavelengths less than approximately 9.5 Å.
Extended Data Figure 4 Beer–Lambert–Bouguer scaling test for Be-tamped iron opacity data.
The transmission should scale according to T2 = T1Nx2/Nx1, where Nx1 and Nx2 are areal densities associated with transmissions T1 and T2. The thick iron sample transmission Tthick (NX ≈ 1.91 × 1018 atoms per cm2) is shown in red (left axis). The average transmission for the two experiments using a thin iron sample (NX ≈ 0.98 × 1018 atoms per cm2) was scaled by the ratio of the areal densities (Tscaled; blue). The error bars represent 1σ uncertainties. A quantitative evaluation is provided by taking the ratio of the transmission difference with the summed 1σ uncertainties (black; right axis). Values below unity (dashed black) satisfy the scaling test.
Extended Data Figure 5 Evaluation of changes in the model–data comparisons at the error bounds determined for the plasma conditions.
The measured iron opacity at Te = 2.11 × 106 K and ne = 3.1 × 1022 cm−3 is denoted with a black line, with error bars corresponding to the 1σ uncertainty. SCRAM23 calculations are shown at the nominal conditions in blue, at the minimum Te, maximum ne in red and at the maximum Te, minimum ne in green. The minimum Te, maximum ne values lead to the lowest ionization and the maximum Te, minimum ne values lead to the highest ionization.
Rights and permissions
About this article
Cite this article
Bailey, J., Nagayama, T., Loisel, G. et al. A higher-than-predicted measurement of iron opacity at solar interior temperatures. Nature 517, 56–59 (2015). https://doi.org/10.1038/nature14048
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature14048
This article is cited by
-
Quantum simulation of exact electron dynamics can be more efficient than classical mean-field methods
Nature Communications (2023)
-
Probing atomic physics at ultrahigh pressure using laser-driven implosions
Nature Communications (2022)
-
Accurate temperature diagnostics for matter under extreme conditions
Nature Communications (2022)
-
Electron localization enhanced photon absorption for the missing opacity in solar interior
Science China Physics, Mechanics & Astronomy (2022)
-
Opacity enhanced by the localization of electrons
Science China Physics, Mechanics & Astronomy (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.