Abstract
Models derived from human pluripotent stem cells that accurately recapitulate neural development in vitro and allow for the generation of specific neuronal subtypes are of major interest to the stem cell and biomedical community. Notch signalling, particularly through the Notch effector HES5, is a major pathway critical for the onset and maintenance of neural progenitor cells in the embryonic and adult nervous system1,2,3. Here we report the transcriptional and epigenomic analysis of six consecutive neural progenitor cell stages derived from a HES5::eGFP reporter human embryonic stem cell line4. Using this system, we aimed to model cell-fate decisions including specification, expansion and patterning during the ontogeny of cortical neural stem and progenitor cells. In order to dissect regulatory mechanisms that orchestrate the stage-specific differentiation process, we developed a computational framework to infer key regulators of each cell-state transition based on the progressive remodelling of the epigenetic landscape and then validated these through a pooled short hairpin RNA screen. We were also able to refine our previous observations on epigenetic priming at transcription factor binding sites and suggest here that they are mediated by combinations of core and stage-specific factors. Taken together, we demonstrate the utility of our system and outline a general framework, not limited to the context of the neural lineage, to dissect regulatory circuits of differentiation.
Similar content being viewed by others
Main
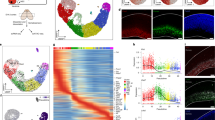
We used the human embryonic stem (ES) cell line WA9 (also known as H9) expressing GFP under the HES5 promoter4 to isolate defined neural progenitor populations of neuroepithelial (NE), early radial glial (ERG), mid radial glial (MRG) and late radial glial (LRG) cells based on their cell morphology and Notch activation state5, as well as long-term neural progenitors (LNP) based on their epidermal growth factor receptor (EGFR) expression5,6 (Fig. 1a and Extended Data Fig. 1a). We took these defined stages to create strand-specific RNA sequencing (RNA-seq) data, chromatin immunoprecipitation followed by sequencing (ChIP-seq) maps for histone H3 lysine 4 monomethylation (H3K4me1), trimethylation (H3K4me3), lysine 27 acetylation (H3K27ac) and H3K27me3 as well as DNA methylation (DNAme) data by whole-genome bisulphite sequencing (WGBS) for the first four stages, and reduced representation bisulphite sequencing (RRBS) for the last two (LRG and LNP) stages (Fig. 1a and Supplementary Table 1).
a, Left, schematic of the cell system. Middle, normalized read-count level for H3K27ac over a 1.4-megabase (Mb) region around the SOX2 locus (chromosome 3: 180,854,252–182,259,543) where SOX2-OS refers to the SOX2 overlapping transcript. ChIP-seq read counts were normalized to 1 million reads and scaled to the same level (1.5) for all tracks shown. Right, additional tracks for H3K4me3, H3K4me1 and H3K27me3 as well as DNAme (scale 0–100%), OTX2 binding and expression covering a 100 kilobase (kb) sub-region (chromosome 3: 181,389,523–181,490,148) of this locus. Histone and RNA-seq data were normalized to 1 million reads and are shown on distinct scales. b, Maximum gene set activity levels shown as z scores for genes expressed in defined brain structures (left) and developmental time points (right) based on the mouse Allen Brain Atlas. Gene set activity was defined as average expression level of all member genes followed by z score computation across all nine cell types. Different., differentiated; LRGdA, LRG-derived astrocyte-like cells; RSP, rostral secondary prosencephalone; Tel, telencephalon; PHy, peduncular (caudal) hypothalamus; p3, hypothalamus; p2, pre-thalamus; p1, pre-tectum; M, midbrain; PPH, prepontine hindbrain; PH, pontine hindbrain; PMH, pontomedullary hindbrain; MH, medullary hindbrain. Developmental times are embryonic days 11.5, 13.5, 15.5 and 18.5 and postnatal days 4, 14 and 28. c, Distribution of DNAme levels for differentially methylated regions (change in methylation ≥0.2, P ≤ 0.01) across state transitions; for instance, distributions for regions gaining methylation in the transition from ES cell to NE (top left) at all stages of differentiation. Distinct methylation level trace plots are shown for regions gaining methylation (left) during the specific transitions (indicated on the side) and loss of methylation (right). Black labelled samples are based on WGBS data and grey colour samples (LRG and LNP) were profiled by RRBS. d, Bar plot showing the number of regions that gain or lose selected modifications across the first four cell-state transitions.
Global transcriptional analysis of the undifferentiated ES cells and the first four neural progenitor cell (NPC) stages identified 3,396 differentially expressed genes (Extended Data Fig. 1b, c and Supplementary Table 2). Pluripotency-associated genes such as OCT4 (also known as POU5F1) and NANOG are, as expected, rapidly downregulated, and pan-neural genes are induced early and maintained throughout the remainder of the differentiation time course (Extended Data Fig. 1c). Using data from the mouse Allen Brain Atlas as an in vivo reference for genes expressed in different brain compartments and developmental stages, we observed a consecutive shift of expression signatures along the NPC differentiation trajectory (Fig. 1b). NE through LRG transcripts suggest anterior neural fates, while the MRG and LRG stages show in addition some posterior identities (Fig. 1b, left). Accordingly, differentiated progeny derived from these populations express deep cortical layer neuronal markers (NEdN and ERGdN) such as FEZF2 and BCL11B and superficial layer neuronal markers (MRGdN) such as POU3F2/POU3F3 and MEF2C (Extended Data Fig. 1d). Progression from early (NE) to late (LRG) stages was also accompanied by a transition from predominantly neurogenic to mainly gliogenic potential, although LRG cells still generate neurons (Extended Data Fig. 1d). This progressive change in NPC identity aligns well with the in vivo order of developmental events7.
In line with these observations, our WGBS data show changes in DNAme that can be separated into two overall patterns. The first is characterized by widespread loss of methylation and retention of the resulting hypomethylated state throughout subsequent differentiation stages (Fig. 1c, top right). This pattern coincides with major cell-fate decisions such as commitment from ES cells to the neural fate and the transition from ERG to MRG, the latter demarcating both peak of neurogenesis and onset of gliogenic potential (Fig. 1c, right middle). The second pattern is defined by a stage-specific loss with subsequent gain at the next stage, as observed during the transition from NE to ERG and also from MRG to LRG (Fig. 1c, right). Conversely, regions gaining DNAme during transition from one stage to another frequently reside in a hypomethylated state in all preceding stages, indicating the possible silencing of stem cell or pan-neural gene regulatory elements (Fig. 1c, left). At the histone modification level we also observed the most widespread changes during the initial neural induction (Fig. 1d); although it is worth noting that the biggest gain of the repressive mark H3K27me3 occurs at the MRG stage.
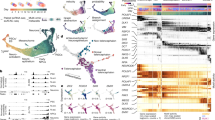
These coordinated epigenetic changes are probably the result of differential transcription factor activity8,9,10,11. We therefore developed a computational method to attribute the genome-wide changes in histone modifications and DNAme at regions termed footprints to particular transcription factors and quantified this remodelling potential (TERA, transcription factor epigenetic remodelling activity; Fig. 2a, Extended Data Fig. 2a and Methods). Notably, the H3K27ac peak set in our NPC model was significantly enriched for single nucleotide polymorphisms previously reported to be implicated in Alzheimer’s disease (P ≤ 0.01) and bipolar disorders (P ≤ 0.01) by genome-wide association studies, suggesting the possibility to utilize this differentiation system as a basis to study the genetic component of complex diseases in vitro12,13. Next, to identify potential key regulators of onset, maintenance and transition through distinct NPC populations, we ranked all motifs and their associated transcription factors based on their TERA scores between consecutive time points (Supplementary Table 3). We then retrieved the transcription factors associated with highest scoring 40 motifs for each cell-state transition (Fig. 2b). This analysis confirmed many well-known key regulators of in vivo neural development and forebrain specification that are induced at the NE stage such as PAX6, OTX2 and FOXG1 (refs 14, 15, 16) as well as various SOX proteins17. Notably, we also found predicted differential activity of distinct downstream components of signalling pathways such as a decrease of SMAD4 activity at the NE stage, consistent with inhibition of TGF-β signalling that promotes neural induction18. Another example that is predicted to be relevant but not limited to the MRG stage is POU3F2, known to be involved in sub-ventricular zone expansion and superficial layer neuronal specification, and TCF12, which is highly expressed in germinal zones during brain development19 (Fig. 2b and Supplementary Table 3).
a, Illustration of epigenomic footprinting across the PAX6 locus (chromosome 11: 31,780,014–31,842,503) for dips in H3K27ac regions (right). Black boxes highlight footprints determined for H3K27ac peaks that harbour various putative transcription factor binding sites based on motif matching. b, The 40 top ranked transcription factors predicted to be activated during the cell-state transition are indicated on the bottom. Colour-coding represents normalized transcription factor epigenetic remodelling scores, averaging over all TERAs based on H3K4me3, H3K4me1, H3K27ac and DNAme. In addition, predictions were filtered for factors expressed at the stage of predicted induction.
To obtain a higher-level overview of the processes and roles associated with the distinct putative regulators, we decomposed the H3K27ac data into seven distinct modules, each corresponding to a unique epigenetic dynamic, genomic region and upstream regulator set (Extended Data Fig. 2b, top). Gene set enrichment analysis20 on the genomic regions associated with each of the distinct modules revealed that the module activated upon neural induction and sustained throughout the MRG stage is strongly associated with stem cell maintenance and differentiation-related processes as well as Notch signalling (Extended Data Fig. 2b; module 2). Further analysis of upstream regulators of this module revealed a strong association with PAX6 and FOXG1, suggesting a role for these factors in the general establishment and maintenance of the telencephalic cortical identity of the NPC states (Extended Data Fig. 2c).
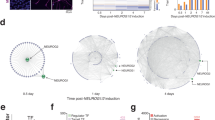
To explore the relevance of predicted factors for each cellular state, we carried out a pooled short hairpin RNA (shRNA) screen against 244 transcription factors and epigenetic modifiers selected based on our RNA-seq data (Fig. 3a, Extended Data Fig. 3a and Supplementary Table 4). In total, we recovered 110 factors whose knockdown had a significant (Fig. 3b, q value ≤ 0.05, mean empirical false discovery rate (FDR) = 0.045, see Methods) negative impact on the number of HES5+ cells in at least one differentiation stage (Supplementary Table 4), with high overlap between the distinct stages (Fig. 3c and Extended Data Fig. 3b). Despite the expected high false-negative rate21 our screen consistently validated more than 50% of the predicted transcription factors with a known motif for the top 20 motifs found at each stage (Fig. 3d and Extended Data Fig. 3c, d), while an expression-based identification yielded only ∼30% recovery (Extended Data Fig. 3c). Among the top factors recovered from the predictions at the early stage (NE and ERG) are the RFX proteins including RFX4, which has been implicated in cortical and brain development22,23, FOXG1, as well as NR2F2, whose paralogue NR2F1 has been shown to serve as an intrinsic factor for early regionalization of the neocortex24,25. Gene set enrichment analysis of putative genomic targets of NR2F2 (see Methods) in the NE cells further expands this role, suggesting involvement in telencephalon, diencephalon and posterior hindbrain development (Supplementary Table 5). At the MRG stage, we recover genes involved in extensive neurogenesis and in commencing early gliogenesis such as NFIA and NFIB, which are involved in both repressing the neuronal progenitor state through Notch signalling concomitantly with activating glial fates26, as well as REST—a major pleotropic epigenetic regulator of neural cell-fate decisions27.
a, Simplified schematic of the pooled shRNA screen (see Extended Data Fig. 3 for more details). Ctrl, control; gDNA, genomic DNA; KD, knockdown; Seq., sequencing. b, Depletion scores for all genes that are significantly reduced (q value ≤ 0.05 for at least two different shRNAs per gene) in at least one stage for fluorescence-activated cell sorting (FACS)-purified HES5+ cells 6 days after knockdown compared to FACS sorted HES5− obtained from the same infection or compared to cells collected 24 h after infection (see Extended Data Fig. 3a). Depletion score indicates the extent to which shRNAs targeting a particular gene were lost during the knockdown period relative to the control, indicating potential relevance of a particular gene for HES5+ maintenance, NPC state progression and proliferation or cell survival. Higher depletion scores (red) indicate stronger reduction in shRNA presence; scores were capped at 1 and computed based on at least three technical replicates per condition. c, Overlap of genes detected to be significantly depleted in the HES5+ population relative to at least one of the control conditions. d, Performance of combined regulator predictions based on TERA ranking averaged over H3K4me3, H3K4me1, H3K27ac and DNAme. Performance is measured as percentage of the top 20 predicted activating or repressing motifs for each stage mapping to transcription factors included in the shRNA library.
Next, we selected a set of 22 core factors with evidence to be functional at all stages as assessed by RNA-seq and the shRNA screening results (Extended Data Fig. 4a and Methods). In order to determine whether the subset of core factors with a DNA binding motif available (10 of 22) exerts the same function at each stage, we performed a co-binding analysis based on the predicted binding sites of 523 transcription factors in dynamically regulated distal H3K27ac footprints. This analysis uncovered highly stage-specific relationships that were also supported by the observed knockdown effect at each stage (Fig. 4a and Extended Data Fig. 4b). Notably, most of the identified co-binding partners are either expressed in a more stage-specific fashion or are only activated in more mature neuronal or glial cell types (Fig. 4b). To further validate some of these findings, we focused on OTX2 due to its high expression in all NPC populations (Fig. 4b) and performed ChIP-seq at the NE and MRG stages. OTX2 was enriched at more targets in NE cells, of which around 35% overlapped with MRG-bound sites (Fig. 4c and Extended Data Fig. 4c). The shared target set is highly enriched for genes involved in stem cell maintenance and differentiation as well as various pro-neural gene sets known to act during advanced stages of forebrain and midbrain progenitor cell maturation (Fig. 4d and Extended Data Fig. 4d). This binding pattern combined with the observation that the OTX2 target gene set reaches peak transcriptional activity in the NEdN and ERGdN populations implies a role for OTX2 in the preparation of pro-neural genes expressed at later stages (Fig. 4d, e). These findings further suggest a model where a core set of transcription factors helps sustain NPC identity throughout the differentiation time course and at the same time participates in the progression and modulation of NPC differentiation potential through cooperation with stage-specific regulators.
a, Predicted significant (P ≤ 0.01, enrichment ≥ 1.5) co-binding relationships in dynamically regulated H3K27ac footprints for a set of 10 transcription factors (bold, core network) required by HES5+ cells in at least two stages. Stage-specific predicted co-binding relationships are indicated in blue (NE), red (ERG) and grey (MRG). All predicted relations were filtered for support by a knockdown effect of each gene at the relevant stage. b, Gene expression patterns shown as z scores for the core network transcription factors as well as all predicted co-binding partners across ES cells, all NPCs and more mature cellular states. c, Venn diagram showing the overlap of OTX2 binding sites determined by ChIP-seq in early NE and MRG cells. d, Gene set enrichment analysis results for OTX2 binding sites in early NE and MRG cells. e, Median expression patterns for ES cells, all NPCs and more mature cell populations shown as z scores for putative downstream target genes of OTX2 binding sites.
To gain a better understanding of how factors that are active at distinct NPC stages contribute to their corresponding neuronal and glial cell propensities, we took advantage of the fact that many transcription factor binding sites exhibit a gain of H3K4me1 and loss of DNAme at the early NPC stages before increased expression of their associated genes in more differentiated cell types (hereafter referred to as epigenetic priming) (Fig. 5a and Extended Data Fig. 5a–c). For instance, we identified three pro-neural factors that show evidence of priming, are induced only at a later stage, and possess transcription factor binding sites that are also significantly (P ≤ 0.05 permutation test) associated with genes differentially expressed at a later stage (Fig. 5a, bold genes). Because these pro-neural genes are not expressed at the early NPC stages but in more mature cell types derived upon mitogen withdrawal, the identification of such priming events highlights that the epigenetic state is useful for predicting regulators relevant at later stages of differentiation. In order to pinpoint transcription factors potentially involved in facilitating these priming events at the respective NPC stages, we determined significant predicted co-binding relationships between the subset of pro-neural transcription factors and factors that in contrast are expressed at the stage of priming (Fig. 5a).
a, Characterization of transcription factors associated with motifs gaining H3K4me1 or losing DNAme at the NE stage before their expression at a later or more differentiated cell state as determined by high TERA scores (bold), termed priming. In addition, significant (P ≤ 0.01, enrichment ≥ 1.5) co-binding relationships with factors expressed at the NE stage are indicated by coloured lines. For each transcription factor (from outer to inner circles, see example to the right for NEUROD4) heat maps indicating the relative expression level as a z score in all cell types as well as normalized TERA scores for H3K27ac, H3K4me3, H3K4me1 and DNAme. b, Top, heat maps depicting the H3K4me1 (left) and H3K27ac (right) enrichment level for predicted NEUROD binding sites at each NPC stage for five distinct dynamic patterns. At the NE and ERG stages, none of the NEUROD family of proteins is expressed at high levels (<3.5 fragments per kilobase of transcript per million mapped reads). Bottom, heat map showing the z scores of the median gene expression levels for predicted NEUROD downstream target genes for each of the five dynamic patterns in the more mature neuron- and astrocyte-like populations.
To specifically investigate the hypothesis that a part of the pro-neural binding site landscape is epigenetically primed at the NPC stages, we focused on predicted NEUROD protein family binding sites within H3K27ac footprints and defined five patterns of H3K27ac and H3K4me1 enrichments across these sites (Fig. 5b). We found that genes associated with predicted NEUROD binding sites in regions gaining H3K27ac or H3K4me1 enrichment at distinct stages of NPC progression are upregulated in more mature populations derived from the respective NPC stage (Fig. 5b and Extended Data Fig. 5d). Consistent with the idea of a comprehensive preparation of the epigenetic landscape during lineage specification, NEUROD binding sites that retain high levels of H3K27ac and H3K4me1 throughout the entire differentiation time course are associated with various anterior and posterior cortical structures as well as early and late developmental time points (Extended Data Fig. 5e).
These results support a model where selected transcription factors at the NPC stage remodel the binding site repertoire for pro-neural factors by preparing the epigenetic landscape at their respective targets. First the general lineage landscape is established upon commitment to the neural fate, followed by the stage-specific modulation of primed pro-neural binding sites. This in turn might serve as a mechanism to restrict their binding space in order to ensure proper neuronal and glial differentiation capacity. In addition to these insights into the epigenetic dynamics during differentiation, we provide a general analysis strategy to interpret differences in epigenetic landscapes based on cell-fate regulatory transcription factors. This strategy can be readily applied to other data sets including the extensive collection of the NIH Roadmap Epigenomics Project (Supplementary Table 3).
Methods
Culturing undifferentiated human ES cells
HES5::eGFP bacterial artificial chromosome transgenic human ES cells (H9; WA9; Wicell) expressing GFP under the HES5 promoter were cultured on mitotically inactivated mouse embryonic fibroblasts (MEFs) (Globalstem). Undifferentiated ES cells were maintained as described previously5 in medium containing DMEM/F12, 20% KSR, 1 mM glutamine, 1% penicillin/streptomycin, non-essential amino acids and β-mercaptoethanol. Undifferentiated ES cells were purified with pluripotency markers Alexa 647-conjugated Tra-1-60 and phycoerythrin-conjugated SSEA-3 (BD Pharmingen).
Neural induction and long-term propagation of NPCs
Neural differentiation of ES cells was performed as described in refs 5,18. In brief, neuroepithelial cells were generated either by monolayer induction—with dissociated ES cells plated on Matrigel (BD biosciences)—or by co-culture on MS5 stromal cells. In both cases neural fate was directed by dual SMAD inhibition protocol18. Neural rosettes generated from both induction methods were harvested mechanically during all stages of differentiation and replated on culture dishes pre-coated with 15 μg ml−1 polyornithine (Sigma), 1 μg ml−1 laminin (BD Biosciences) and 1 μg ml−1 fibronectin (BD Biosciences) (Po/Lam/FN) in N2 medium composed of DMEM/F12 and N2 supplement (Invitrogen). N2 supplement contained insulin, apo-transferin, sodium selenite, putrecine and progesterone. This medium was supplemented with sonic hedgehog (30 ng ml−1), fibroblast growth factor 8 (FGF8; 100 ng ml−1) and brain-derived neurotrophic factor (BDNF) (20 ng ml−1) (all from R&D Systems) to induce and maintain early anterior regionalization of NE cells. These factors were gradually replaced by FGF2 (20 ng ml−1) and EGF (20 ng ml−1) in the following 2 weeks of differentiation in order to maintain a proliferative (FGF and EGF responsive) NPC state. NPCs from all stages were collected at indicated days and FACS purified for HES5::eGFP (NE to LRG) or EGFR for LNPs to purify for the highest NPC state for each stage. NE cells were collected at day 12 of differentiation, ERG cells were collected at day 14, mid-neurogenesis radial glial (MRG) cells were collected at day 35, late-gliogenic radial glial (LRG) cells were collected at day 80, and long-term NPCs (LNP) were collected at day 220. At each stage cells were either split for the next passage or subjected to FACS purification for HES5::eGFP as described. All replating was performed on Po/Lam/FN-coated dishes. For generating mature differentiated populations, HES5+ sorted NPCs were seeded at high density and subjected to mitogen withdrawal differentiation medium for 17 days which included N2 supplemented with ascorbic acid/BDNF (neuronal; NEdN, ERGdN, MRGdN) or 5% fetal bovine serum (FBS) (Invitrogen) (glial; LRGdA). Additional experimental details and in-depth characterization of these cell types are provided in Elkabetz and colleagues (manuscript in preparation).
Chromatin immunoprecipitation followed by sequencing (ChIP-seq)
For the histone ChIP experiments, we used similar approaches to ref. 28. Specifically, around 160,000 cells were crosslinked in 1% formaldehyde for 10 min at 37 °C, followed by quenching with 125 mM glycine for 5 min at 37 °C, washed with PBS containing protease inhibitor (Roche, 04693159001) and flash-frozen in liquid nitrogen. To lyse the cells, we used 1% SDS, 10 mM EDTA and 50 mM Tris-HCl, pH 8.1 complemented with a protease inhibitor. The chromatin was then fragmented with a Branson Sonifier (model S-450D) at 4 °C, and calibrated to a size range of 200 and 800 base pairs (bp). Chromatin was mixed with antibody and incubated at 4 °C overnight. Protein A and Protein G Dynabeads were added to chromatin/antibody mix (Invitrogen, 100-02D and100-07D, respectively) and incubated for 1–2 h at 4 °C. Samples were washed six times with RIPA buffer (10 mM Tris-HCl, pH 8.0, 1 mM EDTA, pH 8.0, 14 mM NaCl, 1% Triton X-100, 0.1% SDS, 0.1% DOC), twice with RIPA buffer containing 500 mM NaCl, twice with LiCl buffer (10 mM TE, 250 mM LiCl, 0.5% NP-40, 0.5% DOC), twice with TE (10 mM Tris-HCl, pH 8.0, 1 mM EDTA), and then eluted in elution buffer (10 mM Tris-Cl, pH 8.0, 5 mM EDTA, 300 mM NaCl, 0.1% SDS, pH 8.0) at 65 °C. Eluate was treated with RNaseA (Roche, 11119915001) and Proteinase K (NEB, P8102S) overnight at 65 °C.
For the OTX2 ChIP cells were collected and crosslinked in 1% formaldehyde for 15 min on ice, quenched with 125 mM glycine for 5 min at room temperature and pelleted. Nuclei were then isolated and chromatin was digested at 37 °C with MNase enzyme until the majority of the DNA was between 50 and 800 bp. Specifically, 25 U and 35 U of MNase enzyme were used to digest NE cells and RNS/RG cells, respectively. The chromatin was then incubated with the antibodies over night at 4 °C and co-immunoprecipitation of antibody–protein complexes was performed with Protein A or G beads for 1–2 h at 4 °C.
All antibody catalogue and lot numbers are listed next to the data set for which they were used in Supplementary Table 1.
ChIP-seq library preparation and sequencing
To extract DNA and create the Illumina libraries we used solid-phase reversible immobilization (SPRI) beads. The SPRI beads were added to the samples, mixed 15 times, and incubated for 2 min at room temperature. Supernatant was extracted from the beads on a magnet (4 min). 70% ethanol was used to wash the beads and then dried for another 4 min. Forty microlitres of EB buffer (10 mM Tris-HCl, pH 8.0) was used to elute the DNA. The next steps of Illumina library construction include end repair, addition of A-base, ligation of barcoded adaptors and PCR enrichment. To minimize the loss of ChIP material throughout this procedure, we used a general SPRI cleanup procedure after each reaction step reusing the same beads. PEG buffer (20% PEG and 2.5 M NaCl) was used to re-bind ChIP material to SPRI following each reaction, and washing and extraction occurred as stated above. The enzymatic reactions were carried as follows: (1) DNA end-repair: Epicentre End-IT Repair kit incubated at room temperature for 45 min; (2) A-base addition: Klenow (3′→5′ exonuclease; New England Biolabs) incubated at 37 °C for 30 min; (3) adaptor ligation: DNA ligase (New England Biolabs) and indexed oligo adaptors and incubated at 25 °C for 15 min, followed by 0.7× SPRI/reaction to remove non-ligated adaptors; (4) PCR enrichment: PCR mastermix (primer set, dNTP mix, Pfu Ultra Buffer (Agilent), Pfu Ultra-II Fusion (Agilent), water), for 20 cycles. The PCR amplified libraries we cleaned up using 0.7× SPRI/reaction (size selection mode) to remove excessive primers. Roughly 5 picomoles of DNA library was then applied to each lane of the flow cell and sequenced on Illumina HiSeq 2000 sequencers according to standard Illumina protocols.
For the OTX2 ChIP, DNA libraries were constructed using standard Illumina protocols for blunt-ending, poly(A) extension, and ligation. MyOne Silane beads (Life Technologies 37002D) were used to purify DNA fragments following each step of the library preparation. Adaptor ligation was performed overnight at 16 °C. Ligated DNA was then PCR amplified and gel size selected for fragments between 150 and 700 bp. Samples were sequenced using Illumina HiSeq at a target sequencing depth of 20 million uniquely aligned reads.
Strand-specific RNA-sequencing library construction
RNA was extracted using the miRNeasy kit (Qiagen, 217004). Poly(A) RNA was isolated using Oligo d (T25) beads (NEB, E7490L). The poly(A) fraction was then fragmented (Invitrogen, AM8740). Fragments smaller than 200 bp were eliminated (Zymo, R1016) and the remaining fraction was treated with FastAP Thermosensitive Alkaline Phosphatase (Thermo Scientific, EF0652) and T4 Polynucleotide Kinase (NEB, M0201L). RNA was then ligated to a RNA adaptor as reporter previously29 using T4 RNA Ligase 1 (NEB, M0204L), which was then used to facilitate complementary DNA synthesis using Affinity Script Multiple Temperature Reverse Transcriptase (Agilent, 600105). More specifically, we used the following adaptors reported in ref. 29: RNA sequencing, RiL-19 3′ RNA adaptor: prArGrArUrCrGrGrArArGrArGrCrGrUrCrGrUrG/ddC; RNA sequencing, AR17 reverse transcription primer: ACACGACGCTCTTCCGA; RNA sequencing, 3Tr3 5′ DNA adaptor: pAGATCGGAAGAGCACACGTCTG/ddC; RNA sequencing, PCR enrichment: AATGATACGGCGACCACCGAGATCTACACTCTTTCCCTACACGACGCTCTTCCGATCTCAAGCAGAAGACGGCATACGAGATNNNNNNNNGTGACTGGAGTTCAGACGTGTGCTCTTCCGATCT.
RNA was then degraded and the cDNA was ligated to a DNA adaptor using T4 RNA Ligase 1 as described previously29. Final library amplification was completed using NEB Next High Fidelity 2X PCT Master Mix (M054L). To clean up the final PCR and removed adaptor dimers, two subsequent 1× and 0.8× SPRI reactions were completed to prepare the final library for sequencing.
Pooled shRNA screen
We selected 244 transcription factors and epigenetic modifiers that were differentially or continuously highly expressed during our in vitro differentiation time course in an otherwise unbiased fashion (Supplementary Table 4). In addition, we included GFP, RFP, LacZ and luciferase as internal controls. We then obtained a sub-pool of the human 45K shRNA pool30 distributed by the Broad Institute Genomic Perturbations Platform and the RNAi Consortium (TRC) against these genes. For each gene, five distinct shRNAs were included as well as five scrambled and three empty control vectors, amounting to a total of 1,230 + 8 shRNAs. The plasmid for shRNA expression under the control of the constitutive U6 shRNA promoter was the lentiviral vector pLKO.1. shRNA pool production and infection conditions were performed as previously described30. Subsequently, we performed calibration experiments to determine to optimal combination of multiplicity of infection (MOI) and puromyocin concentration to ensure efficient selection. We identified MOI 0.4 and 1 μg ml−1 of puromycin as optimal parameters for all stages. We then infected 26 million cells at each stage of NE, ERG and MRG to ensure sufficient shRNA integration events to recover the complexity of the shRNA library. Twenty-four hours post infection and before full expression but after integration of the lentivirus into the genome we collected 3 million cells to determine our baseline shRNA library representation. Subsequently, we subjected the cells to 5 days of puromycin selection and then FACS sorted the resulting populations into HES5+ and HES5− compartments. Next, we assessed the representation of the shRNA library in each of the 9 populations by retrieving all shRNA integration events from genomic DNA isolated from each sample using PCR followed by next-generation sequencing as previously described31. More specifically, we performed two rounds of PCR using the following primers for the primary PCR: primary reverse: CTTTAGTTTGTATGTCTGTTGCTATTAT; primary forward: AATGGACTATCATATGCTTACCGTAAC. For the second, nested PCR we used: nested forward: GGCTTTATATATCTTGTGGAAAGGA; nested reverse: GGATGAATACTGCCATTTGTCTC.
Next, we performed standard Illumina sequencing library construction as outlined above for four technical replicates for NE and MRG and three technical replicates for ERG, each comprising HES5+, HES5− and 24-h control, amounting to a total of 33 libraries. We then sequenced these amplicon libraries on a HiSeq2500 with a PhiX spike-in of 25%.
Individual shRNA validation for OTX2 and PAX6
RNA was extracted using miRNeasy kit (Qiagen) followed by Maxima reverse transcription reaction kit (Fermentas). One nanogram of cDNA was subjected to quantitative PCR (qPCR) using our custom-designed primers and the ABsolute QPCR SYBR Green ROX Mix (ABgene) on a ViiA-7 cycler (ABI). Threshold cycle values were determined in triplicates and presented as average compared to HPRT. Fold changes were calculated using the  method.
method.
WGBS and RRBS library production
WGBS libraries were generated as previously described in ref. 10. RRBS was carried out using the multiplexed, gel-free protocol described in ref. 32.
Data processing
For RNA-seq data processing, reads were trimmed to 80, 60 or 30 bp depending on their per-base quality distribution to achieve maximum alignment rates. Reads were mapped to the human genome (hg19) using TopHat v2.0 (ref. 33) (http://tophat.cbcb.umd.edu) employing the unfiltered gencode.v19.annotation.gtf annotation as the transcriptome reference. TopHat was run with default parameters except for the coverage search being turned off. Transcript expression was estimated with Cuffdiff 2 (ref. 34). The workflow used to analyse the data are described in detail in ref. 35 (alternate protocol B).
WGBS libraries were aligned using BSMap 2.7 (ref. 36) to the hg19/GRCh37 reference assembly. Subsequently, CpG methylation calls were made using custom software as previously described9, excluding duplicate, low-quality reads as well as reads with more than 10% mismatches. Only CpGs with more than 5× coverage were considered for further analysis.
ChIP-seq data were aligned to the hg19/GRCh37 reference genome using MAQ37 version 0.7.1 with default parameter settings or Bowtie 2 version 2.05 (ref. 38). Reads were filtered for duplicates and extended by 200 bp at the end of the read. Visualization of read count data was performed by converting raw BAM files to .tdf files using IGV tools39 and normalizing to 1 million reads. Fragment-length-extended, duplicate and quality-filtered reads were used for subsequent analysis.
shRNA screen data analysis
For the screen data analysis, we followed the protocol outlined in ref. 40 employing the R package limma41. First, we extracted and counted the number of times each shRNA was observed in each library using the shRNA sequence as barcode and the R function processHairpinReads(). Next, we normalized the shRNA counts to the total number of reads observed containing a shRNA to counts per million (cpm) and retained only those shRNAs with more than 0.5 cpm in more than 2 samples. After further quality control showing excellent reproducibility (Extended Data Fig. 3f), we performed differential shRNA count analysis between the HES5+ and 24-h control and the HES5+ and HES5− populations for each stage. To that end we first estimated the dispersion for each condition and then fitted a negative binomial generalized linear model using the R package edgeR. We then conducted a likelihood ratio test for each contrast and only retain those shRNAs as differentially enriched at a FDR ≤ 0.05. To determine genes with significant positive or negative impact on HES5+ maintenance or cell survival, we determined all genes that were targeted by at least two independent shRNAs which showed a significant effect (FDR ≤ 0.05) in the same direction. We then computed a mean effect score in order to rank genes by computing the weighted mean of the log fold change between the two conditions weighted by the log cpm across all significant shRNAs and targeting a particular gene with an effect in the same direction. If an equal number of shRNAs showed a significant effect in positive or negative direction, we classified the gene as not significantly affected. Otherwise we chose the effect direction based on the majority of the shRNAs. We then combined the results from the HES5+ to 24-h control and HES5− comparison into one by taking the maximum mean effect score observed in either comparison. The resulting mean effect scores are then used for visualization and analysis purposes in main text and figures and are reported in Supplementary Table 3. In addition, we also calculated an empirical FDR by determining the fraction of shRNAs with a statistically significant effect based on the generalized linear model but were not expressed based on the RNA-seq data for the condition where the significant effect was observed.
For the TERA validation analysis, we ranked all motifs according to their TERA scores at each stage. Next, we filtered out motifs that were not associated with at least one transcription factor that was covered in our screen design. We then determined the fraction of top 20 motifs (by absolute TERA values) that were linked to transcription factors which showed a significant effect in the corresponding stage-specific shRNA screen. We report this number as the percentage of motifs recovered. Only motif-knockdown results that have a straightforward interpretation were considered as hits. These include: (1) positive TERA score and positive depletion score (gene is involved HES5+ maintenance, progression or cell survival); (2) negative TERA score and negative depletion score (impedes HES5+ maintenance, progression or apoptosis); (3) negative TERA score and positive depletion score (gene is involved HES5+ maintenance, progression or cell survival but most likely acts as a repressor by causing H3K27ac or H3K4me3/1 loss). For the comparison with the expression-based analysis, we ranked all significantly differentially expressed genes by their absolute fold change and determined the fraction of top 20 transcription factors observed among the differentially enriched shRNAs in the screen.
Differential expression analysis
Differential expression analysis was carried out using Cuffidff 2 (ref. 34) and genes differentially expressed at a FDR ≤0.1 for each comparison and a minimal expression level of 1 FPKM in at least one of the conditions were considered. Clustering analysis was performed using the csCluster() function in the cummeRbund42 package version 2.6.1 (http://compbio.mit.edu/cummeRbund/) with the Jensen–Shannon distance as metric. The number of clusters for the NPC set (ESC, NE, ERG, MRG, LRG) and the differentiated populations (NEdN, ERGdN, MRGdN, LRGdA) was determined as the number of clusters between 10 and 20 with the minimum average silhouette width across all clusters. Subsequently, a pseudocount of 1 was added to all FPKM counts followed by a log2 transformation. The resulting values were used for all further expression analysis.
ChIP-seq data analysis and normalization
For H3K27ac and H3K4me3 histone marks, the irreproducible discovery rate (IDR) framework43 with a cutoff of 0.1 in combination with the MACS2 (ref. 44) peak caller version 2.1 was used to identify peaks taking advantage of both replicates for each condition. For MACS2 peak calling, we used an initial P value cutoff of 0.01 and the corresponding whole-cell extract (WCE) control library as background. All IDR peak sets can be obtained from GEO under GSE62193.
For the broad histone marks H3K27me3 and H3K4me1, we first determined all 1-kilobase (kb) tiles of the human genome (hg19) that were significantly enriched over background in at least one of the replicates. To that end we used a Poisson model45 with the WCE as background to model the fragment count distribution in each genomic To that end we defined a nominal P value for enrichment within a given region i in sample k harbouring rik ChIP fragments compared to the WCE control sample l with ril ChIP fragments as P(C ≥ rik) where45:

and eil = ril / λl, λk = (region size) × (total number of ChIP fragments in sample k)/(corrected genome size), λl = (region size) × (total number of ChIP fragments in sample l)/(corrected genome size). In order to account for regions with no or minimal WCE read counts due to sampling, we chose eil = max(eil,1). Resulting P values were adjusted for multiple testing using the Benjamini–Hochberg46 correction and the q value R package47. Only regions significant at a q value ≤0.05 and with an enrichment level over background ≥1.5 were considered to be enriched.
For differential enrichment analysis of histone marks between consecutive conditions, we used the R package diffBind48. To normalize read counts, we used the effective library size, counting only reads in peak regions (either the IDR peaks for H3K27ac, H3K4me3 or the enriched 1-kb tiles for H3K27me3 or H3K4me1). The differential analysis was then conducted using the DBA_DESEQ2 method, taking full advantage of both replicates per condition with the bTagwise parameter set to true. Only regions that were differentially enriched between consecutive conditions at a P value of 0.05 were reported.
In addition, we created a union peak set for each mark separately by joining overlapping peaks/enriched regions in preparation for the TERA analysis. For H3K4me1, we computed the enrichment over the union of all H3K27ac regions since we wanted to focus on much more sharply defined putative enhancer regions for this mark. For H3K27ac, we focused on distal regions only (≥1 kb from nearest TSS) since we were specifically interested in putative enhancer regions for this mark. For H3K4me3, we used the union of all H3K4me3 IDR based peaks regardless of distance, accounting for most promoters and CpG islands. We then determined the enrichment level for all regions in the union set in each replicate across all marks separately. Region enrichment was computed as follows: first, the number of tag counts in each region was determined and normalized to reads per kilobase per million reads (RPKM) sequenced using the full library size of non-duplicate reads. Next, RPKM read counts were divided by the mean RPKM counts across all WCE libraries. Subsequently, the resulting enrichment levels were log2 transformed. Finally, the resulting enrichment values were quantile normalized across the entire data set for each mark separately. The resulting values were then average across replicates to obtain a region × condition normalized enrichment matrix. The resulting matrix was used as input for the TERA analysis. We tested several ChIP normalization strategies by assessing between-replicate correlation and between-condition discriminative power on a large data set of 70 REMC H3K27ac samples and identified this strategy as the best performing one.
Footprinting detection
To determine small regions depleted of histone modifications but surrounded by regions of much greater enrichment, termed footprints, we extended an approach used for the analysis of DNase I hypersensitivity (HS) data49. Our footprints identification algorithm consisted of three main phases. In the first phase, we identify peaks using the IDR framework (see previous section) for H3K27ac and H3K4me3 and use these as baseline regions in which footprints could be detected. In the second phase, we identified footprints located within/around peak regions in the following manner. (1) For each peak, extend by 400 bp from apex in either direction. (2) Split entire resulting region into bins of size 20 bp. (3) Compute number of RPKM counts for a central sliding window across the entire region (shifting by increments of one bin) for different window sizes ranging from two bins to ten bins in increments of one. (4) For each position of the central window and for each window size, compute the following three quantities: Cij − RPKM count for central window at current position i and window size j, Rij − RPKM count for a 200-bp stretch directly to the right of the central window and Lij − RPKM count for a 200-bp stretch directly to the left of the central window. (5) For each resulting position i and window size j compute the depletion score:

With the footprint size normalization factor f = s/b, with s the size of the central window and b the size of the border regions. (6) Identify non-overlapping, non-adjacent footprint candidates starting from small to larger central window sizes and recording footprint candidate if eij > 0 and eij < 1 and Lij > Cij and Rij > Cij, followed by removing all other potential footprints (central window + borders) of larger size overlapping the current candidate. (7) Finally, all resulting candidate footprints with a footprinting score eij ≤ 0.9 were reported.
The latter procedure was carried out for H3K27ac and H3K4me3 independently for each sample. Subsequently, we merged all footprints from individual samples into consensus footprints set for each epigenetic mark separately, collapsing overlapping footprints by taking the union of all regions with non-zero overlap.
Differentially methylated region detection
Differentially methylated region (DMR) detection was carried out as previously described with slight modifications10. Pairwise comparisons of consecutive samples (hESC, NE, ERG, MRG, LRG, LNP) were carried out on a single CpG level using a β-binomial model and the β difference distribution requiring a maximum q value below 0.05 and an absolute methylation difference greater than 0.1. q values were computed based on β-binomial model P values using the Benjamini–Hochberg46 method. Only CpGs covered by at least 5 reads in either sample were considered. Subsequently, differentially methylated CpGs within 500 bp were merged into discrete regions. Differential CpGs without neighbours were embedded into a 100-bp region surrounding each CpG. Next, differential methylation analysis was repeated on the region level using a random effects model. Only regions significant at a P value below 0.01, an absolute methylation difference above 0.2 and containing at least 2 differentially methylated CpGs were considered differentially methylated. These regions were defined as DMRs and used for subsequent analysis. For the DNA methylation analysis in the context of the TERA framework, we restricted our analysis to DMRs consistently covered across all conditions, including those only assessed by RRBS. This left us with 7,929 regions.
Association of genomic regions with genes
We used the R package ChIPpeakAnno50 to associate each region with its nearest ENSEMBL transcription start site and used this mapping for all downstream analysis.
Gene set enrichment analysis
Gene set enrichment analysis for genomic regions was carried out using the GREAT toolbox20 and only categories with q values ≤0.05 for both the hypergeometric and the binomial test as well as a minimal region enrichment level greater than 2 were considered, following the GREAT recommendations. Due to the large number of enriched gene sets, a selected subset of the results is shown in the different figures. In addition, we used the Allen Brain Atlas51 to determine enrichment for distinct brain structures and developmental time points. To that end we derived gene sets from the brain atlas data in the following fashion.
We obtained in situ hybridization counts for the developing mouse brain at 7 distinct fetal time points and 11 different brain substructures through direct correspondence with http://www.alleninstitute.org. Specifically, we investigated the following structures: rostral secondary prosencephalone (RSP), telencephalon (Tel), peduncular (caudal) hypothalamus (PHy), hypothalamus (p3), pre-thalamus (p2), pre-tectum (p1), midbrain (M), prepontine hindbrain (PPH), pontine hindbrain (PH), pontomedullary hindbrain (PMH), medullary hindbrain (MH); and time points: embryonic (E) day 11.5, E13.5, E15.5 and E18.5 as well postnatal (P) P4, P14 and P28. In total, we had 14,585 measurements for 2,105 different genes across these different regions and time points. In order to define sets of genes characteristic for each combination of time point and structure, we computed the z scores as well as the maximum observed variation for each gene across the entire matrix of structure and developmental time point combinations. Only genes that exhibited a maximum observed variation (maximum activity − minimum activity) ≥1 were considered for gene set definition. Next, we mapped all mouse genes to their human orthologues using the biomaRt database. Finally, we defined gene sets for each region–time-point combination using genes that exhibited a z score ≥2 in that particular combination. Since the Allen Brain Atlas gene sets are defined for each developmental time point and regional identity, we next simplified the visualization by focusing either exclusively on structures or developmental time points. Therefore, we determined the gene set with the maximum gene set activity at each differentiation stage across all gene sets associated with distinct developmental time points for each structure separately. Similarly, we determined the gene set with maximum activity for each developmental time point now taking the maximum across all structures at each stage. The gene set activity was determined as the mean log2-transformed expression level of all gene set members in for each condition.
Motif library construction and mapping to transcription factors
We combined the position weight matrices (PWM) from Transfac professional database52 (2011) with the PWM collection reported in ref. 53, only retaining motifs annotated for Homo sapiens or mouse. To eliminate redundant motifs, we determined pairwise motif similarities for all resulting 1,886 PWMs using the TOMTOM54 program which is part of the MEME55 suite with default parameters. Next, we compiled a pseudo-distance matrix based on the resulting pairwise motif similarities. As a proxy for motif similarity, we used the log10-transformed TOMTOM q value which was capped at ten. To convert the resulting motif similarities into a distance matrix, we inverted the scale by subtracting the transformed q values from ten. We then used the resulting matrix to perform hierarchical clustering with Euclidean distance and Ward’s method. Finally, we employed the cutree() function with a threshold of seven to partition the resulting clustering dendrogram into discrete clusters of motifs. For each cluster, we then determined the motif with the highest complexity based on the relative entropy compared to a genome background model with the following base frequencies: A = 0.2725, C = 0.189, G = 0.189 and T = 0.2728. Only motifs with a relative entropy greater than or equal to eight were retained for subsequent analysis. After identification of the candidate with the highest complexity for each motif cluster, we assigned all genes mapping to any motif in each corresponding cluster to the cluster representative motif. This lead to a final motif list of 557 motifs. To obtain a more quantitative association of each motif with its linked genes, we computed the epigenetic transcription factor activity (ETFA) scores across 70 REMC H3K27ac or H3K4me3 cell types and correlated the results with RNA-seq expression data across 40 cell types. This analysis gave rise to a correlation matrix containing the Pearson correlation coefficient of each motif with its linked genes. This matrix was used in combination with the plain gene mapping reported in primary motif sources. For Fig. 2b, we uniquely map each motif to a corresponding linked gene by computing an association score as the product of the absolute Pearson correlation coefficient and the average gene expression level of the corresponding gene. We then chose the gene with the highest association score. For motifs without an entry in the H3K27ac correlation matrix (due to the inability to determine suitable GEV parameters on the REMC data set), we chose the gene with the highest gene expression level. In Fig. 2b, only genes expressed with at least 10 FKPM in the respective condition are considered. We then report the genes mapping to the 40 motifs for each condition, where TERA scores of motifs mapping the same gene were averaged.
In Figs 4 and 5, we incorporated the results of the shRNA screen to uniquely map motifs applying the aforementioned mapping strategy only on the genes identified as hits. If it did not map to any gene hit by the screen, we used the standard assignment strategy outlined above.
Identification of putative transcription factor binding sites
To determine putative binding sites in a given genomic region, we used a biophysical model of transcription factor affinities to DNA56,57 to determine putative binding to our footprint sets. This biophysical model requires the training of generalized extreme value (GEV) distributions of binding affinities based on a PWM matrix for each transcription factor and each set of genomic regions in order to generate a suitable background model. In order to take the distinct properties of footprints determined from different epigenetic marks into account, we determined the GEV parameters for footprints arising from H3K27ac, H3K4me3 and DNAme using the framework outlined in refs 56, 57. The resulting three binding matrices were then filtered for minimal significant binding affinity at P values below 0.05. All other entries with higher P values were set to one. Next, we took the negative log10 of the entire matrix as a quantitative measure of binding affinity in subsequent analysis.
Inference of transcription factor activities based on epigenetic data
To infer transcription factor epigenetic remodelling activities (TERA), we first computed ETFA from our epigenetic data. To that end, we first focused on motif activity analysis and associated each motif in a second step with its corresponding transcription factor. For each epigenetic mark, we used the normalized epigenetic enrichment scores as well as DMRs with a minimal DNA methylation difference of at least 0.2 and covered consistently in all data sets. For the DNA methylation data, we inverted the scale to obtain demethylation scores (1 = fully demethylated, 0 = fully methylated) since usually the demethylated states coincides with gene regulatory element activity. To determine the unobserved activity of a transcription factor binding motif, we took advantage of recent developments in the microarray field58,59 and adapted this approach to epigenetic data. To that end we modelled the enrichment level yit of a particular epigenetic mark at genomic region i and time point t as a linear function of the unknown transcription factor activities. Considering p predictor variables (epigenetic motif/transcription factor activities) and k time points we describe the unknown transcription factor activities X as a p × k matrix. Incorporating all regions n meeting the above listed criteria, we employ the linear model  with the observed matrix of epigenetic enrichment scores Y (n × k), a constant offset matrix A (n × k), the connectivity matrix B (n × p), describing the filtered binding affinities for all transcription factor motifs to all regions and an error term matrix E. Subsequently, we followed the approach outlined in ref. 58 and applied partial least square (PLS) regression and specifically the SIMPLs algorithm60 to determine the unknown transcription factor motif activities. The idea in PLS is to employ a linear dimensionality reduction
with the observed matrix of epigenetic enrichment scores Y (n × k), a constant offset matrix A (n × k), the connectivity matrix B (n × p), describing the filtered binding affinities for all transcription factor motifs to all regions and an error term matrix E. Subsequently, we followed the approach outlined in ref. 58 and applied partial least square (PLS) regression and specifically the SIMPLs algorithm60 to determine the unknown transcription factor motif activities. The idea in PLS is to employ a linear dimensionality reduction  , where the p predictors in X are mapped onto c ≤ rank(X) ≤ min(p,n) latent components T (n × c matrix), and to compute the weight matrix R not only based on the data matrix B but explicitly taking into account the response matrix Y. The latter strategy maximizes predictive power even for a small number of latent components.
, where the p predictors in X are mapped onto c ≤ rank(X) ≤ min(p,n) latent components T (n × c matrix), and to compute the weight matrix R not only based on the data matrix B but explicitly taking into account the response matrix Y. The latter strategy maximizes predictive power even for a small number of latent components.
In order to determine the number of latent components for each epigenetic mark and genomic context, we performed cross validation by randomly partitioning the data set 20 times into two-thirds training and one-third test sets. We then chose the number of components such that it minimized the prediction error. The corresponding analysis methodology was implemented in the statistical programming language R adapting the implementation provided in ref. 58. To assess the significance of the resulting ETFA scores, we performed a permutation test by randomly permuting the epigenetic enrichment scores for each gene regulatory element and recomputed the ETFA values on the permuted values. This process is repeated 100 times. Positive ETFA scores are considered to be insignificant and set to 0 if a greater ETFA score is observed more than once on the randomly permuted set and vice versa for negative ETFA scores.
Finally, we determined the TERA scores by computing the differential ETFA scores between consecutive conditions. These scores were determined by subtracting ETFA scores of consecutive time points from each other. Subsequently, we assessed the significance of this difference using a permutation test by randomly permuting the epigenetic enrichment scores across all regions, re-computing the ETFA scores for each conditions and assessing the TERA score between consecutive conditions for each motif. Positive TERA scores are considered to be insignificant and set to 0 if a greater TERA score is observed more than once on the randomly permuted set and vice versa for negative TERA scores.
Co-binding analysis
Co-binding relationships were evaluated using an empirical approach with the entire set of footprints for each epigenetic mark as background. For a given factor i, we determined the footprints set Fi relevant for the current comparison (for example, changing their epigenetic state in particular cell state transition) that were predicted to contain a transcription factor binding site based on the binding model outlined above. Next, we computed the frequency of motif co-occurrence  across Fi for all other motifs j in our database. To generate a proper null distribution, we randomly sampled K = 100 standardized footprint sets Gk each of size |Fi| from the entire footprint collection for the epigenetic mark under study and computed the same test statistic
across Fi for all other motifs j in our database. To generate a proper null distribution, we randomly sampled K = 100 standardized footprint sets Gk each of size |Fi| from the entire footprint collection for the epigenetic mark under study and computed the same test statistic  on these sets. Finally, we determined an empirical P value and enrichment over the control based on these quantities by counting the number of instances for which
on these sets. Finally, we determined an empirical P value and enrichment over the control based on these quantities by counting the number of instances for which  :
:

Only co-binding relationships significant at P values ≤0.01, a median enrichment over the control ≥1.5 and an expression level ≥2 FPKM in at least one condition were retained. For the core factor co-binding analysis, the predicted co-binding relationships were additionally filtered for support by the knockdown data at the stage of predicted co-binding
Validation analysis on ENCODE data
To validate the outlined strategy in silico we took advantage of publically available transcription factor ChIP-seq data in four cell lines from the ENCODE61 project as well as H3K27ac and RNA-seq data for 70 cell types from the REMC project. We downloaded H3K27ac data as well as processed transcription factor binding data from the ENCODE project for the cell line K562 since abundant transcription factor binding data based on ChIP-seq was available. In addition, this data set has been successfully used in several studies to benchmark transcription factor binding predictions62,63. We then applied our TERA pipeline to the H3K27ac data sets and computed the transcription factor binding affinities for a set of 557 distinct motifs. With these data sets at hand, we computed the true-positive rate (TPR), the false-positive rate (FPR) and the positive predictive values (PPV) for all transcription factors that could be matched to at least one motif with available binding affinities (46 out of 117). In the event that one factor matched multiple motifs, we chose the motif with the highest area under the curve.
GWAS analysis
The GWAS analysis was conducted using 11,027 GWAS SNPs from the GWAS catalogue (August 2013). We sought to determine whether the H3K27ac-positive regions identified in the NPC populations were enriched for any GWAS SNP class with respect to a H3K27ac peak compendium across many different tissues. To determine a proper background distribution we randomly sampled K = 1000 equally sized peak sets from H3K27ac-based footprints identified across 70 epigenome roadmap data sets. Prior to further analysis, we normalized the size of each peak all sets by extending it by 250 bp in each direction from the center coordinate. Next, we determined the overlap with GWAS SNPs for control and neural H3K27ac footprint sets. Subsequently, we computed an empirical P value for each trait/disease i in the catalogue by determining the number of trait associated SNPs  overlapping with each control region set Cj and the number overlapping with the corresponding footprint set si according to
overlapping with each control region set Cj and the number overlapping with the corresponding footprint set si according to

Determination of core network
The core network was defined as those transcription factors that were differentially expressed during neural induction from ES cell to NE and not differentially expressed between consecutive stages of NE, ERG and MRG. We did not consider the LRG stage. Furthermore, we required that each factor was expressed at least 10 FPKM or more in NE, ERG and MRG and that its mean normalized, maximum difference in expression levels between any of the stages did not exceed one standard deviation computed across the entire data set of 9 cell types. In addition, we also considered genes that were not differentially expressed between any consecutive stages including the ESC stage but fulfilled all other criteria. This identification procedure gave rise to the candidate list of core factors. We then intersected this list with the results of our shRNA screen and retained only those factors that were significantly depleted in the HES5+ population relative to the respective HES5− or control population in at least two stages. Since the literature supported a role for PAX6 and OTX2 for which our shRNAs showed no effect due to the pooled setup or absent knockdown (Fig. 3f and Extended Data Fig. 3g), we included these genes as well. Finally, we merged this list will all transcription factors that were depleted in our shRNA screen at all three stages in the HES5+ population relative to the controls and were expressed at least at 10 FPKM or more in NE, ERG and MRG. This algorithm yielded a list of 22 transcription factors or epigenetic modifiers (Fig. 4a). We then carried out co-binding analysis in H3K27ac footprints dynamically regulated at each stage in order to obtain putative stage-specific co-binding relationships. To determine significant co-binding events, we used the permutation procedure outlined above and retained all co-binding partners with an enrichment over the control ≥1.5 that were significant at P ≤ 0.01 that were also identified as a significant hit in the shRNA screen at the particular stage under investigation.
Transcription factor binding site priming analysis
To determine transcription factors associated with transcription factor binding site priming before factor activation, we determined all transcription factors at each stage that were significantly upregulated at the consecutive NPC time point or induced in the corresponding more differentiated cell type (q value ≤ 0.1) and showed an increase in H3K4me1- or DNAme-derived TERA activity at the current stage under investigation. In addition, we required that the corresponding motif did not map to any transcription factor that was expressed more than 3.5 FPKM at the current stage under investigation. From this list, we picked the pro-neural genes NEUROD4, ASCL2 and NFIX for further investigation due to their literature support for their pro-neural functions. Finally, we required that the potential downstream target genes were significantly enriched for differentially regulated genes at the next NPC stage or in the corresponding more differentiated cell types. To that end, we determined all putative transcription factor binding sites for a particular factor in dynamically regulated H3K27ac or H3K4me1 footprints at the stage of potential priming. We then associated each of these putative binding sites with the nearest TSS and determined the number of differentially expressed genes for each factor. To assess significance, we randomly drew 100 sets of equally sized H3K27ac footprints with no motif of the factor under investigation and determined the number of differentially expressed genes for the subsequent stages. Only factors that exhibited more differentially expressed genes compared to the control sets in more than 99% of the cases were retained.
Next, we performed co-binding analysis in H3K27ac peaks differentially regulated between the ES cell and NE stage as outlined above and display the top 10 co-binding relationships per factor with an odds-ratio ≥1.5 that were significant at a permutation-test-based P ≤ 0.01 in Fig. 5a.
Accession codes
Primary accessions
Gene Expression Omnibus
Data deposits
All data are available from the GEO database under accession number GSE62193, the NIH Roadmap (http://www.roadmapepigenomics.org/data) and NCBI Epigenomics portal (http://www.ncbi.nlm.nih.gov/epigenomics).
References
Imayoshi, I., Sakamoto, M., Yamaguchi, M., Mori, K. & Kageyama, R. Essential roles of Notch signaling in maintenance of neural stem cells in developing and adult brains. J. Neurosci. 30, 3489–3498 (2010)
Shimojo, H., Ohtsuka, T. & Kageyama, R. Dynamic expression of notch signaling genes in neural stem/progenitor cells. Front. Neurosci. 5, 78 (2011)
Carlén, M. et al. Forebrain ependymal cells are Notch-dependent and generate neuroblasts and astrocytes after stroke. Nature Neurosci. 12, 259–267 (2009)
Placantonakis, D. G. et al. BAC transgenesis in human embryonic stem cells as a novel tool to define the human neural lineage. Stem Cells 27, 521–532 (2009)
Elkabetz, Y. et al. Human ES cell-derived neural rosettes reveal a functionally distinct early neural stem cell stage. Genes Dev. 22, 152–165 (2008)
Lafaille, F. G. et al. Impaired intrinsic immunity to HSV-1 in human iPSC-derived TLR3-deficient CNS cells. Nature 491, 769–773 (2012)
Lui, J. H. et al. Development and evolution of the human neocortex. Cell 46, 18–36 (2011)
Voss, T. C. & Hager, G. L. Dynamic regulation of transcriptional states by chromatin and transcription factors. Nature Rev. Genet. 15, 69–81 (2014)
Ziller, M. J. et al. Charting a dynamic DNA methylation landscape of the human genome. Nature 500, 477–481 (2013)
Gifford, C. A. et al. Transcriptional and epigenetic dynamics during specification of human embryonic stem cells. Cell 153, 1149–1163 (2013)
Arnold, P. et al. Modeling of epigenome dynamics identifies transcription factors that mediate Polycomb targeting. Genome Res. 23, 60–73 (2012)
Maurano, M. T. et al. Systematic localization of common disease-associated variation in regulatory DNA. Science 337, 1190–1195 (2012)
Claussnitzer, M. et al. Leveraging cross-species transcription factor binding site patterns: from diabetes risk loci to disease mechanisms. Cell 156, 343–358 (2014)
Götz, M., Stoykova, A. & Gruss, P. Pax6 controls radial glia differentiation in the cerebral cortex. Neuron 21, 1031–1044 (1998)
Hanashima, C., Li, S. C., Shen, L., Lai, E. & Fishell, G. Foxg1 suppresses early cortical cell fate. Science 303, 56–59 (2004)
Martinez-Barbera, J. P. et al. Regionalisation of anterior neuroectoderm and its competence in responding to forebrain and midbrain inducing activities depend on mutual antagonism between OTX2 and GBX2. Development 128, 4789–4800 (2001)
Pevny, L. H., Sockanathan, S., Placzek, M. & Lovell-Badge, R. A role for SOX1 in neural determination. Development 125, 1967–1978 (1998)
Chambers, S. M. et al. Highly efficient neural conversion of human ES and iPS cells by dual inhibition of SMAD signaling. Nature Biotechnol. 27, 275–280 (2009)
Uittenbogaard, M. & Chiaramello, A. Expression of the bHLH transcription factor Tcf12 (ME1) gene is linked to the expansion of precursor cell populations during neurogenesis. Gene Expr. Patterns 1, 115–121 (2002)
McLean, C. Y. et al. GREAT improves functional interpretation of cis-regulatory regions. Nature Biotechnol. 28, 495–501 (2010)
Sims, D. et al. High-throughput RNA interference screening using pooled shRNA libraries and next generation sequencing. Genome Biol. 12, R104 (2011)
Blackshear, P. J. et al. Graded phenotypic response to partial and complete deficiency of a brain-specific transcript variant of the winged helix transcription factor RFX4. Development 130, 4539–4552 (2003)
Zarbalis, K. et al. A focused and efficient genetic screening strategy in the mouse: identification of mutations that disrupt cortical development. PLoS Biol. 2, e219 (2004)
Zhou, C., Tsai, S. Y. & Tsai, M. J. COUP-TFI: an intrinsic factor for early regionalization of the neocortex. Genes Dev. 15, 2054–2059 (2001)
Faedo, A. et al. COUP-TFI coordinates cortical patterning, neurogenesis, and laminar fate and modulates MAPK/ERK, AKT, and β-catenin signaling. Cereb. Cortex 18, 2117–2131 (2008)
Piper, M. et al. NFIA controls telencephalic progenitor cell differentiation through repression of the Notch effector Hes1. J. Neurosci. 30, 9127–9139 (2010)
Qureshi, I. A., Gokhan, S. & Mehler, M. F. REST and CoREST are transcriptional and epigenetic regulators of seminal neural fate decisions. Cell Cycle 9, 4477–4486 (2010)
Garber, M. et al. A high-throughput chromatin immunoprecipitation approach reveals principles of dynamic gene regulation in mammals. Mol. Cell 47, 810–822 (2012)
Engreitz, J. M. et al. The Xist lncRNA exploits three-dimensional genome architecture to spread across the X chromosome. Science 341, 1237973 (2013)
Luo, B. et al. Highly parallel identification of essential genes in cancer cells. Proc. Natl Acad. Sci. USA 105, 20380–20385 (2008)
Strezoska, Ž. et al. Optimized PCR conditions and increased shRNA fold representation improve reproducibility of pooled shRNA screens. PLoS ONE 7, e42341 (2012)
Boyle, P. et al. Gel-free multiplexed reduced representation bisulfite sequencing for large-scale DNA methylation profiling. Genome Biol. 13, R92 (2012)
Trapnell, C., Pachter, L. & Salzberg, S. L. TopHat: discovering splice junctions with RNA-seq. Bioinformatics 25, 1105–1111 (2009)
Trapnell, C. et al. Differential analysis of gene regulation at transcript resolution with RNA-seq. Nature Biotechnol. 31, 46–53 (2013)
Trapnell, C. et al. Differential gene and transcript expression analysis of RNA-seq experiments with TopHat and Cufflinks. Nature Protocols 7, 562–578 (2012)
Xi, Y. & Li, W. BSMAP: whole genome bisulfite sequence MAPping program. BMC Bioinformatics 10, 232 (2009)
Li, H., Ruan, J. & Durbin, R. Mapping short DNA sequencing reads and calling variants using mapping quality scores. Genome Res. 18, 1851–1858 (2008)
Langmead, B. & Salzberg, S. L. Fast gapped-read alignment with Bowtie 2. Nature Methods 9, 357–359 (2012)
Thorvaldsdóttir, H., Robinson, J. T. & Mesirov, J. P. Integrative Genomics Viewer (IGV): high-performance genomics data visualization and exploration. Brief. Bioinform. 14, 178–192 (2013)
Dai, Z. et al. shRNA-seq data analysis with edgeR. F1000Res. 3, 95 (2014)
Smyth, G. K. in Bioinformatics and Computational Biology Solutions Using R and Bioconductor Statistics for Biology and Health (ed. Gentleman, R. ) (Springer, 2005)
Goff, L., Trapnell, C. & Kelley, D. cummeRbund: Analysis, Exploration, Manipulation, and Visualization of Cufflinks High-Throughput Sequencing Data. http://compbio.mit.edu/cummeRbund/ (2012)
Li, Q. H., Brown, J. B., Huang, H. Y. & Bickel, P. J. Measuring reproducibility of high-throughput experiments. Ann. App. Stat. 5, 1752–1779 (2011)
Zhang, Y. et al. Model-based analysis of ChIP-seq (MACS). Genome Biol. 9, R137 (2008)
Mikkelsen, T. S. et al. Comparative epigenomic analysis of murine and human adipogenesis. Cell 143, 156–169 (2010)
Benjamini, Y. & Hochberg, Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. B 57, 289–300 (1995)
Dabney, A. & Storey, J. D. qvalue: Q-value estimation for false discovery rate control. R package version 1.40.0. (2013)
Ross-Innes, C. S. et al. Differential oestrogen receptor binding is associated with clinical outcome in breast cancer. Nature 481, 389–393 (2012)
Neph, S. et al. An expansive human regulatory lexicon encoded in transcription factor footprints. Nature 489, 83–90 (2012)
Zhu, L. J. et al. ChIPpeakAnno: a Bioconductor package to annotate ChIP-seq and ChIP-chip data. BMC Bioinformatics 11, 237 (2010)
Thompson, C. L. et al. A high-resolution spatiotemporal atlas of gene expression of the developing mouse brain. Neuron 83, 309–323 (2014)
Fogel, G. B. et al. A statistical analysis of the TRANSFAC database. Biosystems 81, 137–154 (2005)
Jolma, A. et al. DNA-binding specificities of human transcription factors. Cell 152, 327–339 (2013)
Gupta, S., Stamatoyannopoulos, J. A., Bailey, T. L. & Noble, W. S. Quantifying similarity between motifs. Genome Biol. 8, R24 (2007)
Bailey, T. L., Williams, N., Misleh, C. & Li, W. W. MEME: discovering and analyzing DNA and protein sequence motifs. Nucleic Acids Res. 34, W369–W373 (2006)
Manke, T., Roider, H. G. & Vingron, M. Statistical modeling of transcription factor binding affinities predicts regulatory interactions. PLOS Comput. Biol. 4, e1000039 (2008)
Manke, T., Heinig, M. & Vingron, M. Quantifying the effect of sequence variation on regulatory interactions. Hum. Mutat. 31, 477–483 (2010)
Boulesteix, A. L. & Strimmer, K. Predicting transcription factor activities from combined analysis of microarray and ChIP data: a partial least squares approach. Theor. Biol. Med. Model. 2, 23 (2005)
Boulesteix, A. L. & Strimmer, K. Partial least squares: a versatile tool for the analysis of high-dimensional genomic data. Brief. Bioinform. 8, 32–44 (2007)
de Jong, S. Simpls: an alternative approach to partial least-squares regression. Chemometr. Intell. Lab. 18, 251–263 (1993)
The ENCODE Project Consortium An integrated encyclopedia of DNA elements in the human genome. Nature 489, 57–74 (2012)
Sherwood, R. I. et al. Discovery of directional and nondirectional pioneer transcription factors by modeling DNase profile magnitude and shape. Nature Biotechnol. 32, 171–178 (2014)
Thurman, R. E. et al. The accessible chromatin landscape of the human genome. Nature 489, 75–82 (2012)
Acknowledgements
We would like to thank all members of the Meissner and Elkabetz laboratories; we thank L. Studer (Sloan-Kettering Institute) for the HES5::eGFP reporter line; we also thank F. Kelley and other members of the Broad Sequencing Platform, J. Doench and members of the Genome Perturbation Platform at the Broad Institute, D.-A. Landau for critical reading of the manuscript, as well as to I. Shur and O. Sagi-Assif at Tel Aviv University for their extensive FACS operation. We also thank L. Gaffney for graphical support. This work was funded by the NIH Common Fund (U01ES017155), NHGRI (HG006911), NIGMS (P01GM099117), the New York Stem Cell Foundation, the Israel Science Foundation (ISF) (1126/10, 1710/10) and a Marie Curie International Reintegration Grant (IRG277151). A.Go. is supported by the Charles H. Hood Foundation and A.M. is a New York Stem Cell Foundation Robertson Investigator.
Author information
Authors and Affiliations
Contributions
The study was designed by M.J.Z., Y.E. and A.M. R.E. and Y.E. developed the NPC system, R.E. and Y.Y. performed consecutive cell isolation, propagation and differentiation and conducted the shRNA screen with Y.E.. M.J.Z. performed the analysis and designed the shRNA screen. W.M. and J.L.R. helped with RNA-seq data processing and analysis. J.D. performed transcription factor ChIP-seq experiments. R.P. and C.A.G. performed RNA-seq library construction. R.P. and D.C. performed shRNA library construction. T.S.M. provided experimental advice. R.I., J.X. and A.Go. conducted histone ChIP-seq experiments. H.G. performed WGBS and RRBS library construction, A.Gn. and A.M. supervised the DNA methylation profiling, C.E. and B.E.B. provided experimental input and advice for the ChIP-seq experiments. A.M.T. provided the transcription factor ChIP-seq protocol. O.K. assisted in the design of analytical methods. M.J.Z, Y.E. and A.M. interpreted the data and wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
Extended Data Figure 1 Isolation and characterization of ES-cell-derived neural progenitor cells.
This figure relates to Fig. 1 in the main text. a, Schematic of our differentiation model including the specific days of sample collection. Human ES cells were differentiated into NE cells using dual inhibition of TGF-β and bone morphogenetic protein followed by the transition to neural base media. Subsequently, sonic hedgehog and FGF8 are used to transition to the ERG stage. For the rest of the differentiation experiment the cells were constantly maintained in FGF2 and EGF2 neural base media to reach the MRG stage after 35 days (D35), the LRG stage after 80 and the LNP stage after about 200 days of in vitro culture. Cell type names indicated in red were profiled for gene expression, histone modifications as well as DNAme by WGBS, while names shown in grey for gene expression only and names in black for DNAme by RRBS only. NSB, noggin/SB-431542; SHH, sonic hedgehog; FGF, fibroblast growth factor; EGF, epidermal growth factor. b, Hierarchical clustering for all RNA-seq data sets collapsing replicates using the Jensen–Shannon (JS) divergence as a metric c, Gene expression patterns shown as z scores for all differentially expressed genes (q value ≤ 0.1) across ES cells and four neural precursor differentiation stages for genes expressed at ≥ 1 FPKM in at least one stage (n = 20,306). Genes were grouped into 18 clusters based on minimal average silhouette width using partitioning around medoids (PAM) clustering and Jensen–Shannon divergence as a metric. Pie charts below indicate the fraction of up- (red) and downregulated (green) genes during each transition. d, Gene expression patterns shown as z scores for all significantly differentially expressed genes (q value ≤ 0.1) across four more mature cell populations obtained through differentiation of NE, ERG or MRG cells to neuronal-like cells (NE/ERG/MRGdN) and astrocyte-like cells (LRGdA) derived from the LRG stage. Genes were grouped into 12 clusters based on minimal average silhouette width using PAM clustering and the Jensen–Shannon divergence as a metric.
Extended Data Figure 2 Epigenetic dynamics and transcription factor footprints.
This figure relates to Fig. 2 in the main text. a, Median TPR (red), FPR (blue) and PPV (black) for n = 46 transcription factors with matching motif for H3K27ac footprints (n = 27,292) in K562 cells as a function of confidence in predicted binding (−log10 P value). True positives were defined as predicted binding events overlapping with peaks determined by ChIP-seq and false positives accordingly. The entire set of positives was defined as all transcription factor ChIP-seq peaks for a particular factor that overlapped with any H3K27ac footprint. b, Top, decomposition of H3K27ac dynamics into 7 distinct modules based on PLS regression. Colours indicate median epigenetic enrichment level of gene regulatory elements assigned to each module for each cellular state for H3K27ac. Bottom, selected gene set enrichment analysis results for gene regulatory elements associated with each module. c, Connectivity matrix showing the association strength of each of the factors listed in Fig. 2b with each of the 7 modules identified by the partial least square (PLS) regression.
Extended Data Figure 3 Functional validation using a pooled shRNA screen.
This figure relates to Fig. 3 in the main text. a, Detailed outline of the pooled shRNA screen. Each stage (NE, ERG and MRG) was infected with an optimized virus titre aiming for an average of one shRNA integration per cell. Immediately after infection, cells were subjected to puromycin (puro) selection and bulk population material was collected 24 h after infection and before efficient shRNA knockdown. Five days after infection and selection, cells were FACS-sorted for HES5–GFP and both GFP+ and GFP− cells were collected for analysis. Subsequently, gDNA was extracted and all integrated shRNAs were amplified by PCR for each population separately. The resulting material was then used to construct libraries for next-generation sequencing to count the number of shRNA integrations for each shRNA in each cell population. b, Overlap of genes identified to facilitate HES5+ cell maintenance, progression or proliferation determined by genes with at least two shRNAs significantly (q ≤ 0.05) over-represented in the HES5+ population with respect to the 24-h or HES5− control. c, Regulator predictions based on differential gene expression. Performance is measured as percentage of the top 20 differentially expressed factors for each stage for those the transcription factors included in the shRNA library. d, Regulator predictions based on TERA ranking for H3K4me3, H3K4me1, H3K27ac or DNAme. Performance is measured as percentage of the top 20 predicted activating or repressive motifs for each stage mapping to a transcription factor included in the shRNA library. e, Detailed heat map showing the top 30 predicted motifs and corresponding transcription factors differentially active between consecutive differentiation stages based on the combined TERA scores for H3K27ac, H3K4me3, H3K4me1 and DNAme. In addition, knockdown results as depletion scores (green/red heat map) obtained at each stage are shown on the right. f, Heat map showing the pairwise Pearson correlation coefficient (PCC) of the log2 read-count normalized shRNA libraries across all conditions and technical replicates. g, Individual validation for shRNAs against OTX2 and PAX6 at the NE stage, which showed no effect in our pooled screening approach at any stage. Shown are qPCR levels for OTX2 or PAX6, HES5 and puromycin relative to HPRT. Each gene was measured in an independent knockdown experiment for a pool of the five shRNAs against PAX6 (blue), OTX2 (green), lacZ (orange) as well as the uninfected control (red).
Extended Data Figure 4 Co-binding analysis.
This figure relates to Fig. 4 in the main text. a, Gene expression levels reported as z scores for core network transcription factors and epigenetic modifiers with and without a known DNA binding motif. b, Illustration of predicted significant co-binding relationships (P ≤ 0.01, enrichment ≥ 1.5) of core factors (rows) with more stage-specific or pro-neuronal/glial factors (columns). Colour coding indicates whether binding is stage specific or occurs at multiple stages. c, Overlap of predicted binding sites in dynamic putative enhancer regions based on H3K27ac for OTX2 in NE and ERG. d, Gene set enrichment analysis results for predicted OTX2 binding sites in dynamic putative enhancer regions at the NE and MRG stage.
Extended Data Figure 5 Epigenetic priming.
This figure relates to Fig. 5 in the main text. a, TERA scores for H3K27ac, H3K4me3, H3K4me1 and DNAme for transcription factors showing evidence of priming (top, bold) and transcription factors predicted to significantly co-occur in these primed binding sites. b, Gene expression levels shown as z scores for primed and co-binding transcription factors from panel a. c, Detailed predicted co-binding relationship (P ≤ 0.01, enrichment ≥ 1.5) of primed transcription factors (columns) with significantly associated co-binding factors (rows). d, Illustration of a potential priming event and the associated predicted target gene at the ATOH1 locus (chromosome 4: 94,740–94,800). For each stage, H3K27ac, H3K27me3 and DNAme patterns are shown along with predicted NEUROD binding sites (black boxes) in putative gene regulatory elements marked by a loss of DNAme (highlighted by the grey bars). e, Gene set enrichment analysis results for predicted NEUROD binding sites split up by dynamic patterns defined in the top of Fig. 5b. Binding sites in patterns 3 and 4 showed no significant enrichment.
Supplementary information
Supplementary Table 1
Summary statistics and overview of all datasets generated for this study. (XLSX 18 kb)
Supplementary Table 2
Gene expression levels in FPKM for all RNA-Seq datasets used in this study based GENCODE annotations. (XLSX 6280 kb)
Supplementary Table 3
TERA scores for all epigenetic marks individually as well as averaged for all NPC stages as well as H3K27ac and H3K4me3 based scores for most REMC cell types. (XLSX 2026 kb)
Supplementary Table 4
shRNA screen raw data and evaluation. (XLSX 309 kb)
Supplementary Table 5
Gene set enrichment analysis for predicted individual TF binding in dynamically regulated H3K27ac regions at each stage. (XLSX 31362 kb)
Rights and permissions
About this article
Cite this article
Ziller, M., Edri, R., Yaffe, Y. et al. Dissecting neural differentiation regulatory networks through epigenetic footprinting. Nature 518, 355–359 (2015). https://doi.org/10.1038/nature13990
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature13990
This article is cited by
-
BAF45D-binding to HOX genes was differentially targeted in H9-derived spinal cord neural stem cells
Scientific Reports (2024)
-
Epigenetic and transcriptional regulations prime cell fate before division during human pluripotent stem cell differentiation
Nature Communications (2023)
-
Ectoderm-derived frontal bone mesenchymal stem cells promote traumatic brain injury recovery by alleviating neuroinflammation and glutamate excitotoxicity partially via FGF1
Stem Cell Research & Therapy (2022)
-
Massively parallel reporter perturbation assays uncover temporal regulatory architecture during neural differentiation
Nature Communications (2022)
-
Astroblastomas exhibit radial glia stem cell lineages and differential expression of imprinted and X-inactivation escape genes
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.