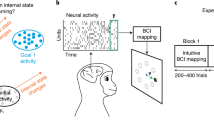
Abstract
Learning, whether motor, sensory or cognitive, requires networks of neurons to generate new activity patterns. As some behaviours are easier to learn than others1,2, we asked if some neural activity patterns are easier to generate than others. Here we investigate whether an existing network constrains the patterns that a subset of its neurons is capable of exhibiting, and if so, what principles define this constraint. We employed a closed-loop intracortical brain–computer interface learning paradigm in which Rhesus macaques (Macaca mulatta) controlled a computer cursor by modulating neural activity patterns in the primary motor cortex. Using the brain–computer interface paradigm, we could specify and alter how neural activity mapped to cursor velocity. At the start of each session, we observed the characteristic activity patterns of the recorded neural population. The activity of a neural population can be represented in a high-dimensional space (termed the neural space), wherein each dimension corresponds to the activity of one neuron. These characteristic activity patterns comprise a low-dimensional subspace (termed the intrinsic manifold) within the neural space. The intrinsic manifold presumably reflects constraints imposed by the underlying neural circuitry. Here we show that the animals could readily learn to proficiently control the cursor using neural activity patterns that were within the intrinsic manifold. However, animals were less able to learn to proficiently control the cursor using activity patterns that were outside of the intrinsic manifold. These results suggest that the existing structure of a network can shape learning. On a timescale of hours, it seems to be difficult to learn to generate neural activity patterns that are not consistent with the existing network structure. These findings offer a network-level explanation for the observation that we are more readily able to learn new skills when they are related to the skills that we already possess3,4.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Krakauer, J. W. & Mazzoni, P. Human sensorimotor learning: adaptation, skill, and beyond. Curr. Opin. Neurobiol. 21, 636–644 (2011)
Ranganathan, R., Wieser, J., Mosier, K. M., Mussa-Ivaldi, F. A. & Scheidt, R. A. Learning redundant motor tasks with and without overlapping dimensions: facilitation and interference effects. J. Neurosci. 34, 8289–8299 (2014)
Thoroughman, K. & Taylor, J. Rapid reshaping of human motor generalization. J. Neurosci. 25, 8948–8953 (2005)
Braun, D., Mehring, C. & Wolpert, D. Structure learning in action. Behav. Brain Res. 206, 157–165 (2010)
Ganguly, K. & Carmena, J. M. Emergence of a stable cortical map for neuroprosthetic control. PLoS Biol. 7, e1000153 (2009)
Fetz, E. E. Operant conditioning of cortical unit activity. Science 163, 955–958 (1969)
Jarosiewicz, B. et al. Functional network reorganization during learning in a brain-computer interface paradigm. Proc. Natl Acad. Sci. USA 105, 19486–19491 (2008)
Hwang, E. J., Bailey, P. M. & Andersen, R. A. Volitional control of neural activity relies on the natural motor repertoire. Curr. Biol. 23, 353–361 (2013)
Rouse, A. G., Williams, J. J., Wheeler, J. J. & Moran, D. W. Cortical adaptation to a chronic micro-electrocorticographic brain computer interface. J. Neurosci. 33, 1326–1330 (2013)
Engelhard, B., Ozeri, N., Israel, Z., Bergman, H. & Vaadia, E. Inducing γ oscillations and precise spike synchrony by operant conditioning via brain-machine interface. Neuron 77, 361–375 (2013)
Cunningham, J. P. & Yu, B. M. Dimensionality reduction for large-scale neural recordings. Nature Neurosci http://dx.doi.org/10.1038/nn.3776
Mazor, O. & Laurent, G. Transient dynamics versus fixed points in odor representations by locust antennal lobe projection neurons. Neuron 48, 661–673 (2005)
Mante, V., Sussillo, D., Shenoy, K. V. & Newsome, W. T. Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature 503, 78–84 (2013)
Rigotti, M. et al. The importance of mixed selectivity in complex cognitive tasks. Nature 497, 585–590 (2013)
Churchland, M. M. et al. Neural population dynamics during reaching. Nature 487, 51–56 (2012)
Luczak, A., Barthó, P. & Harris, K. D. Spontaneous events outline the realm of possible sensory responses in neocortical populations. Neuron 62, 413–425 (2009)
Shadmehr, R., Smith, M. & Krakauer, J. Error correction, sensory prediction, and adaptation in motor control. Annu. Rev. Neurosci. 33, 89–108 (2010)
Li, C. S., Padoa-Schioppa, C. & Bizzi, E. Neuronal correlates of motor performance and motor learning in the primary motor cortex of monkeys adapting to an external force field. Neuron 30, 593–607 (2001)
Salinas, E. Fast remapping of sensory stimuli onto motor actions on the basis of contextual modulation. J. Neurosci. 24, 1113–1118 (2004)
Picard, N., Matsuzaka, Y. & Strick, P. L. Extended practice of a motor skill is associated with reduced metabolic activity in M1. Nature Neurosci. 16, 1340–1347 (2013)
Rioult-Pedotti, M.-S., Friedman, D. & Donoghue, J. P. Learning-induced LTP in neocortex. Science 290, 533–536 (2000)
Peters, A. J., Chen, S. X. & Komiyama, T. Emergence of reproducible spatiotemporal activity during motor learning. Nature 510, 263–267 (2014)
Paz, R., Natan, C., Boraud, T., Bergman, H. & Vaadia, E. Emerging patterns of neuronal responses in supplementary and primary motor areas during sensorimotor adaptation. J. Neurosci. 25, 10941–10951 (2005)
Durstewitz, D., Vittoz, N. M., Floresco, S. B. & Seamans, J. K. Abrupt transitions between prefrontal neural ensemble states accompany behavioral transitions during rule learning. Neuron 66, 438–448 (2010)
Jeanne, J. M., Sharpee, T. O. & Gentner, T. Q. Associative learning enhances population coding by inverting interneuronal correlation patterns. Neuron 78, 352–363 (2013)
Gu, Y. et al. Perceptual learning reduces interneuronal correlations in macaque visual cortex. Neuron 71, 750–761 (2011)
Ingvalson, E. M., Holt, L. L. & McClelland, J. L. Can native Japanese listeners learn to differentiate /r–l/ on the basis of F3 onset frequency? Biling. Lang. Cogn. 15, 255–274 (2012)
Park, D. C. et al. The impact of sustained engagement on cognitive function in older adults: the Synapse Project. Psychol. Sci. 25, 103–112 (2014)
Boden, M. A. Creativity and artificial intelligence. Artif. Intell. 103, 347–356 (1998)
Ajemian, R., D’Ausilio, A., Moorman, H. & Bizzi, E. A theory for how sensorimotor skills are learned and retained in noisy and nonstationary neural circuits. Proc. Natl Acad. Sci. USA 110, E5078–E5087 (2013)
Tkach, D. C., Reimer, J. & Hatsopoulos, N. G. Observation-based learning for brain-machine Interfaces. Curr. Opin. Neurobiol. 18, 589–594 (2008)
Velliste, M., Perel, S., Spalding, M. C., Whitford, A. S. & Schwartz, A. B. Cortical control of a prosthetic arm for self-feeding. Nature 453, 1098–1101 (2008)
Santhanam, G. et al. Factor-analysis methods for higher-performance neural prostheses. J. Neurophysiol. 102, 1315–1330 (2009)
Yu, B. M. et al. Gaussian-process factor analysis for low-dimensional single-trial analysis of neural population activity. J. Neurophysiol. 102, 614–635 (2009)
Dempster, A. P., Laird, N. M. & Rubin, D. B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. [Ser A] 39, 1–38 (1977)
Wu, W., Gao, Y., Bienenstock, E., Donoghue, J. P. & Black, M. J. Bayesian population decoding of motor cortical activity using a Kalman filter. Neural Comput. 18, 80–118 (2006)
Gilja, V. et al. A high-performance neural prosthesis enabled by control algorithm design. Nature Neurosci. 15, 1752–1757 (2012)
Björck, Å. & Golub, G. H. Numerical methods for computing angles between linear subspaces. Math. Comput. 27, 579–594 (1973)
Fitts, P. M. The information capacity of the human motor system in controlling the amplitude of movement. J. Exp. Psychol. Gen. 47, 381–391 (1954)
Acknowledgements
We thank A. Barth, C. Olson, D. Sussillo, R. J. Tibshirani and N. Urban for discussions; S. Flesher for help with data collection and R. Dum for advice on array placement. This work was funded by NIH NICHD CRCNS R01-HD071686 (A.P.B. and B.M.Y.), NIH NINDS R01-NS065065 (A.P.B.), Burroughs Wellcome Fund (A.P.B.), NSF DGE-0549352 (P.T.S.) and NIH P30-NS076405 (Systems Neuroscience Institute).
Author information
Authors and Affiliations
Contributions
P.T.S., K.M.Q., M.D.G., S.M.C., B.M.Y. and A.P.B. designed the experiments. S.I.R. and E.C.T.-K. implanted the arrays. P.T.S. collected and analysed the data. P.T.S., B.M.Y. and A.P.B. wrote the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
Extended Data Figure 1 Performance during baseline blocks.
a, Histograms of success rate during the baseline blocks on days when the perturbation would later be within-manifold (red) and outside-manifold (blue) for monkey J (top) and monkey L (bottom). For days with multiple perturbation sessions, the data are coloured according to the first perturbation type. Dashed lines, means of distributions; solid lines, mean ± s.e.m. b, Histograms of target acquisition time during baseline blocks. Number of days for panels a and b: within-manifold perturbations, n = 27 (monkey J), 14 (monkey L); outside-manifold perturbations, n = 31 (monkey J), 14 (monkey L). c, Sample cursor trajectories to all eight targets. At the beginning of each day, the monkeys used the intuitive mapping for 250–400 trials. The monkeys were able to use these mappings to control the cursor proficiently from the outset (as measured by success rate and acquisition time). On all sessions, the success rates were near 100%, and the acquisition times were between 800 and 1,000 ms. No performance metrics during the baseline blocks were significantly different between within-manifold perturbation sessions and outside-manifold perturbation sessions (P > 0.05; success rate, Wilcoxon rank-sum test; acquisition time, two-tailed Student's t-test).
Extended Data Figure 2 Changes in success rate and acquisition time during perturbation blocks.
In Fig. 2d, we quantified the amount of learning in each session using a single metric that combined improvements in success rate and acquisition time. Here, we consider each metric separately. In each comparison, better performance is to the right. a, Change in success rate from the first 50-trial bin in the perturbation block to the bin with the best performance. The change in success rate was significantly greater for within-manifold perturbations than for outside-manifold perturbations for monkey J (top, P < 10−3, t-test). For monkey L (bottom), the change in success rate was greater for within-manifold perturbations than for outside-manifold perturbations, and the difference approached significance (P = 0.088, t-test). b, Change in acquisition time from the first 50-trial bin in the perturbation block to the bin with the best performance. For both monkeys, the change in acquisition time for within-manifold perturbations was significantly greater than for outside-manifold perturbations (monkey J (top), P < 10−4, t-test; monkey L (bottom), P = 0.0014, t-test). Note that a negative acquisition time change indicates performance improvement (that is, targets were acquired faster). Number of within-manifold perturbations, n = 28 (monkey J), 14 (monkey L); outside-manifold perturbations, n = 39 (monkey J), 15 (monkey L).
Extended Data Figure 3 After-effects during washout blocks.
After 600 (monkey J) or 400 (monkey L) trials using the perturbed mapping, we re-introduced the intuitive mapping to observe any after-effects of learning. We measured the after-effect as the size of the performance impairment at the beginning of the washout block in the same way that we measured the performance impairment at the beginning of the perturbation block. A larger after-effect indicates more learning had occurred in response to the perturbation. For monkey J (left), the after-effect was significantly larger for within-manifold perturbations (red) than for outside-manifold perturbations (blue) (Wilcoxon rank-sum test, P < 10−3). For monkey L (right), the trend is in the same direction as monkey J, but the effect did not achieve significance (Wilcoxon rank-sum test, P > 0.05). These data are consistent with the hypothesis that relatively little learning occurred during the outside-manifold perturbations in comparison to the within-manifold perturbations. Number of within-manifold perturbations, n = 27 (monkey J), 14 (monkey L); outside-manifold perturbations, n = 33 (monkey J), 15 (monkey L).
Extended Data Figure 4 Learning did not improve over sessions.
It might have been that, over the course of weeks and months, the animals improved at learning to use perturbed mappings, either one type or both types together. This did not occur. Within-manifold perturbations showed more learning than outside-manifold perturbations across the duration of experiments. Animals did not get better at learning to use either type of perturbation separately (red and blue regression lines, F-test, P > 0.05 for all relationships) nor when considering all sessions together (black regression line, F-test for linear regression, P > 0.05). Same number of sessions as in Extended Data Fig. 2. Each point corresponds to one session.
Extended Data Figure 5 Hand speeds during BCI control and hand control.
We loosely restrained the monkeys’ arms to the chair’s armrests during experiments. The monkeys minimally moved their hands, but the movements did not approach the limits of the restraints. a, Average hand speeds across all trials in all sessions for the baseline blocks (left column), within-manifold perturbation blocks (middle column), and outside-manifold perturbation blocks (right column) for monkey J (top row) and monkey L (bottom row). b, Average hand speed during a typical point-to-point reaching task (monkey L). Thus, the hand movements for the BCI tasks are substantially smaller than for the reaching task.
Extended Data Figure 6 Accounting for within-class differences in learning.
a, Relation between amount of learning and initial impairment in performance for monkey J (top) and monkey L (bottom). Each point corresponds to one session. Lines are linear regressions for the within-manifold perturbations and outside-manifold perturbations. *Slope significantly different than 0 (F-test for linear regression, P < 0.05). b, Relation between amount of learning and mean principal angles between control spaces for perturbed and intuitive mappings. c, Relation between amount of learning and mean required preferred direction (PD) change. Same number of sessions as in Extended Data Fig. 2. Figure 3 showed that the properties of the perturbed mappings (other than whether their control spaces were within or outside the intrinsic manifold) could not account for differences in learning between the two types of perturbation. However, as is evident in Fig. 2d, within each type of perturbation, there was a range in the amount of learning, including some outside-manifold perturbations that were learnable5,7. In this figure, we examined whether learning within each perturbation type could be accounted for by considering other properties of the perturbed mapping. We regressed the amount of learning within each perturbation type against the various properties we considered in Fig. 3. Panel a shows the initial performance impairment could explain a portion of the variability of learning within both classes of perturbation for monkey J. That monkey showed more learning on sessions when the initial performance impairment was larger. For monkey L, the initial performance impairment could account for a portion of the within-class variation in learning only for outside-manifold perturbations; this monkey showed less learning when the initial performance impairment was larger. We speculate that monkey J was motivated by more difficult perturbations while monkey L could be frustrated by more difficult perturbations. Panel b shows that the mean principal angles between control planes were related to learning within each class of perturbation for monkey L only. Larger mean principal angles between the control planes led to less learning. Panel c shows that the required PD changes were not related to learning for either type of perturbation for both monkeys. This makes the important point that we were unable to account for the amount of learning by studying each neural unit individually.
Extended Data Figure 7 Offline analyses of intrinsic manifold properties.
a, The intrinsic dimensionalities for all sessions for monkey J (left) and monkey L (right). For both monkeys, the intrinsic dimensionalities were not significantly different between days when we performed within-manifold perturbations and days when we performed outside-manifold perturbations (t-test, P > 0.05). Dashed lines, means of distributions; solid lines, mean ± s.e.m. Same number of days as in Extended Data Fig. 1. b, Relation between intrinsic dimensionality and the number of data points used to compute intrinsic dimensionality. For each of 5 days (one curve per day), we computed the intrinsic dimensionality using 25%, 50%, 75% and 100% of the total number of data points recorded during the calibration block. As the number of data points increased, our estimate of the intrinsic dimensionality increased in a saturating manner. c, Tuning of the raw factors. These plots exhibit the factors that were shuffled during within-manifold perturbations. We show for one typical day the average factors ( ) corresponding to the ten dimensions of the intrinsic manifold over a time interval of 700 ms beginning 300 ms after the start of every trial. Within each row, the coloured bars indicate the mean ± standard deviation of the factors for each target. The line in each circular inset indicates the axis of ‘preferred’ and ‘null’ directions of the factor. The length of the axis indicates the relative depth of modulation. The tuning is along an axis (rather than in a single direction) because the sign of a given factor is arbitrary. d, Tuning of the orthonormalized factors. Same session and plotting format as c. The orthonormalized dimensions are ordered by the amount of shared variance explained, which can be seen by the variance of the factors across all targets. Note that the axes of greatest variation are separated by approximately 90° for orthonormalized dimensions 1 and 2. This property was typical across days. The retrospective estimate of intrinsic dimensionality (Fig. 4 and Extended Data Fig. 7a) may depend on the richness of the behavioural task, the size of the training set (Extended Data Fig. 7b), the number of neurons, the dimensionality reduction method and the criterion for assessing dimensionality. Thus, the estimated intrinsic dimensionality should only be interpreted in the context of these choices, rather than in absolute terms. The key to the success of this experiment was capturing the prominent patterns by which the neural units co-modulate. As shown in Fig. 4d, the top several dimensions capture the majority of the shared variance. Thus, we believe that our main results are robust to the precise number of dimensions used during the experiment. Namely, the effects would have been similar as long as we had identified at least a small handful of dimensions. Given the relative simplicity of the BCI and observation tasks, our estimated intrinsic dimensionality is probably an underestimate (that is, a richer task may have revealed a larger set of co-modulation patterns that the circuit is capable of expressing). Even so, our results suggest that the intrinsic manifold estimated in the present study already captures some of the key constraints imposed by the underlying neural circuitry. The probable underestimate of the ‘true’ intrinsic dimensionality may explain why a few nominal outside-manifold perturbations were readily learnable (Fig. 2d). It is worth noting that improperly estimating the intrinsic dimensionality would only have weakened the main result. If we had overestimated the dimensionality, then some of the ostensible within-manifold perturbations would actually have been outside-manifold perturbations. In this case, the amount of learning would tend to be erroneously low for nominal within-manifold perturbations. If we had underestimated the dimensionality, then some of the ostensible outside-manifold perturbations would actually have been within-manifold perturbations. In this case, the amount of learning would tend to be erroneously high for outside-manifold perturbations. Both types of estimation error would have decreased the measured difference in the amount of learning between within-manifold perturbation and outside-manifold perturbations.
) corresponding to the ten dimensions of the intrinsic manifold over a time interval of 700 ms beginning 300 ms after the start of every trial. Within each row, the coloured bars indicate the mean ± standard deviation of the factors for each target. The line in each circular inset indicates the axis of ‘preferred’ and ‘null’ directions of the factor. The length of the axis indicates the relative depth of modulation. The tuning is along an axis (rather than in a single direction) because the sign of a given factor is arbitrary. d, Tuning of the orthonormalized factors. Same session and plotting format as c. The orthonormalized dimensions are ordered by the amount of shared variance explained, which can be seen by the variance of the factors across all targets. Note that the axes of greatest variation are separated by approximately 90° for orthonormalized dimensions 1 and 2. This property was typical across days. The retrospective estimate of intrinsic dimensionality (Fig. 4 and Extended Data Fig. 7a) may depend on the richness of the behavioural task, the size of the training set (Extended Data Fig. 7b), the number of neurons, the dimensionality reduction method and the criterion for assessing dimensionality. Thus, the estimated intrinsic dimensionality should only be interpreted in the context of these choices, rather than in absolute terms. The key to the success of this experiment was capturing the prominent patterns by which the neural units co-modulate. As shown in Fig. 4d, the top several dimensions capture the majority of the shared variance. Thus, we believe that our main results are robust to the precise number of dimensions used during the experiment. Namely, the effects would have been similar as long as we had identified at least a small handful of dimensions. Given the relative simplicity of the BCI and observation tasks, our estimated intrinsic dimensionality is probably an underestimate (that is, a richer task may have revealed a larger set of co-modulation patterns that the circuit is capable of expressing). Even so, our results suggest that the intrinsic manifold estimated in the present study already captures some of the key constraints imposed by the underlying neural circuitry. The probable underestimate of the ‘true’ intrinsic dimensionality may explain why a few nominal outside-manifold perturbations were readily learnable (Fig. 2d). It is worth noting that improperly estimating the intrinsic dimensionality would only have weakened the main result. If we had overestimated the dimensionality, then some of the ostensible within-manifold perturbations would actually have been outside-manifold perturbations. In this case, the amount of learning would tend to be erroneously low for nominal within-manifold perturbations. If we had underestimated the dimensionality, then some of the ostensible outside-manifold perturbations would actually have been within-manifold perturbations. In this case, the amount of learning would tend to be erroneously high for outside-manifold perturbations. Both types of estimation error would have decreased the measured difference in the amount of learning between within-manifold perturbation and outside-manifold perturbations.
Source data
Rights and permissions
About this article
Cite this article
Sadtler, P., Quick, K., Golub, M. et al. Neural constraints on learning. Nature 512, 423–426 (2014). https://doi.org/10.1038/nature13665
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature13665
This article is cited by
-
3D spatiotemporally scalable in vivo neural probes based on fluorinated elastomers
Nature Nanotechnology (2024)
-
Neurobiologically realistic neural network enables cross-scale modeling of neural dynamics
Scientific Reports (2024)
-
Arithmetic value representation for hierarchical behavior composition
Nature Neuroscience (2023)
-
Residual dynamics resolves recurrent contributions to neural computation
Nature Neuroscience (2023)
-
Dynamical flexible inference of nonlinear latent factors and structures in neural population activity
Nature Biomedical Engineering (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.