Abstract
Laser cooling and trapping are central to modern atomic physics. The most used technique in cold-atom physics is the magneto-optical trap (MOT), which combines laser cooling with a restoring force from radiation pressure. For a variety of atomic species, MOTs can capture and cool large numbers of particles to ultracold temperatures (less than ∼1 millikelvin); this has enabled advances in areas that range from optical clocks to the study of ultracold collisions, while also serving as the ubiquitous starting point for further cooling into the regime of quantum degeneracy. Magneto-optical trapping of molecules could provide a similarly powerful starting point for the study and manipulation of ultracold molecular gases. The additional degrees of freedom associated with the vibration and rotation of molecules, particularly their permanent electric dipole moments, allow a broad array of applications not possible with ultracold atoms1. Spurred by these ideas, a variety of methods has been developed to create ultracold molecules. Temperatures below 1 microkelvin have been demonstrated for diatomic molecules assembled from pre-cooled alkali atoms2,3, but for the wider range of species amenable to direct cooling and trapping, only recently have temperatures below 100 millikelvin been achieved4,5. The complex internal structure of molecules complicates magneto-optical trapping. However, ideas and methods necessary for creating a molecular MOT have been developed6,7,8,9,10,11 recently. Here we demonstrate three-dimensional magneto-optical trapping of a diatomic molecule, strontium monofluoride (SrF), at a temperature of approximately 2.5 millikelvin, the lowest yet achieved by direct cooling of a molecule. This method is a straightforward extension of atomic techniques and is expected to be viable for a significant number of diatomic species6,7. With further development, we anticipate that this technique may be employed in any number of existing and proposed molecular experiments, in applications ranging from precision measurement12 to quantum simulation13 and quantum information14 to ultracold chemistry15.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Carr, L., DeMille, D., Krems, R. & Ye, J. Cold and ultracold molecules: science, technology and applications. New J. Phys. 11, 055049 (2009)
Ni, K.-K. et al. A high phase-space-density gas of polar molecules. Science 322, 231–235 (2008)
Danzl, J. G. et al. An ultracold high-density sample of rovibronic ground-state molecules in an optical lattice. Nature Phys. 6, 265–270 (2010)
Zeppenfeld, M. et al. Sisyphus cooling of electrically trapped polyatomic molecules. Nature 491, 570–573 (2012)
Stuhl, B. K. et al. Evaporative cooling of the dipolar hydroxyl radical. Nature 492, 396–400 (2012)
Di Rosa, M. D. Laser-cooling molecules. Eur. Phys. J. D 31, 395–402 (2004)
Stuhl, B. K., Sawyer, B. C., Wang, D. & Ye, J. Magneto-optical trap for polar molecules. Phys. Rev. Lett. 101, 243002 (2008)
Shuman, E. S., Barry, J. F., Glenn, D. R. & DeMille, D. Radiative force from optical cycling on a diatomic molecule. Phys. Rev. Lett. 103, 223001 (2009)
Shuman, E. S., Barry, J. F. & DeMille, D. Laser cooling of a diatomic molecule. Nature 467, 820–823 (2010)
Barry, J. F., Shuman, E. S., Norrgard, E. B. & DeMille, D. Laser radiation pressure slowing of a molecular beam. Phys. Rev. Lett. 108, 103002 (2012)
Hummon, M. T. et al. 2D magneto-optical trapping of diatomic molecules. Phys. Rev. Lett. 110, 143001 (2013)
The ACME Collaboration. Order of magnitude smaller limit on the electric dipole moment of the electron. Science 343, 269–272 (2014)
Micheli, A., Brennen, G. K. & Zoller, P. A toolbox for lattice-spin models with polar molecules. Nature Phys. 2, 341–347 (2006)
DeMille, D. Quantum computation with trapped polar molecules. Phys. Rev. Lett. 88, 067901 (2002)
Krems, R. V. Cold controlled chemistry. Phys. Chem. Chem. Phys. 10, 4079–4092 (2008)
Hutzler, N. R., Lu, H.-I. & Doyle, J. M. The buffer gas beam: an intense, cold, and slow source for atoms and molecules. Chem. Rev. 112, 4803–4827 (2012)
Prentiss, M. G., Bigelow, N. P., Shahriar, M. S. & Hemmer, P. R. Forces on three-level atoms including coherent population trapping. Opt. Lett. 16, 1695–1697 (1991)
Nasyrov, K. et al. Magneto-optical trap operating on a magnetically induced level-mixing effect. Phys. Rev. A 64, 023412 (2001)
Prentiss, M., Cable, A., Bjorkholm, J. E., Chu, S. & Raab, E. L. Atomic-density-dependent losses in an optical trap. Opt. Lett. 13, 452–454 (1988)
Flemming, J. et al. Magneto-optical trap for sodium atoms operating on the D1 line. Opt. Commun. 135, 269–272 (1997)
Tiwari, V. B., Singh, S., Rawat, H. S. & Mehendale, S. C. Cooling and trapping of 85Rb atoms in the ground hyperfine F = 2 state. Phys. Rev. A 78, 063421 (2008)
Berkeland, D. J. & Boshier, M. G. Destabilization of dark states and optical spectroscopy in Zeeman-degenerate atomic systems. Phys. Rev. A 65, 033413 (2002)
Rio Fernandes, D. et al. Sub-Doppler laser cooling of fermionic 40K atoms in three-dimensional gray optical molasses. Europhys. Lett. 100, 63001 (2012)
Metcalf, H. J. & van der Straten, P. Laser Cooling and Trapping (Springer, 1999)
Wallace, C. D. et al. Measurements of temperature and spring constant in a magneto-optical trap. J. Opt. Soc. Am. B 11, 703–711 (1994)
Chieda, M. A. & Eyler, E. E. Prospects for rapid deceleration of small molecules by optical bichromatic forces. Phys. Rev. A 84, 063401 (2011)
DeMille, D., Barry, J. F., Edwards, E. R., Norrgard, E. B. & Steinecker, M. H. On the transverse confinement of radiatively slowed molecular beams. Mol. Phys. 111, 1805–1813 (2013)
Hunter, L. R., Peck, S. K., Greenspon, A. S., Alam, S. S. & DeMille, D. Prospects for laser cooling TlF. Phys. Rev. A 85, 012511 (2012)
Tarbutt, M. R., Sauer, B. E., Hudson, J. J. & Hinds, E. A. Design for a fountain of YbF molecules to measure the electron's electric dipole moment. New J. Phys. 15, 053034 (2013)
Chin, C., Flambaum, V. V. & Kozlov, M. G. Ultracold molecules: new probes on the variation of fundamental constants. New J. Phys. 11, 055048 (2009)
Barry, J. F. Laser Cooling and Slowing of a Diatomic Molecule. PhD thesis (Yale Univ., 2013)
Barry, J. F., Shuman, E. S. & DeMille, D. A bright, slow cryogenic molecular beam source for free radicals. Phys. Chem. Chem. Phys. 13, 18936–18947 (2011)
Klöter, B., Weber, C., Haubrich, D., Meschede, D. & Metcalf, H. Laser cooling of an indium atomic beam enabled by magnetic fields. Phys. Rev. A 77, 033402 (2008)
Lett, P. D. et al. Observation of atoms laser cooled below the Doppler limit. Phys. Rev. Lett. 61, 169–172 (1988)
Chu, S., Hollberg, L., Bjorkholm, J. E., Cable, A. & Ashkin, A. Three-dimensional viscous confinement and cooling of atoms by resonance radiation pressure. Phys. Rev. Lett. 55, 48–51 (1985)
Lett, P. D. et al. Optical molasses. J. Opt. Soc. Am. B 6, 2084–2107 (1989)
Hänggi, P., Talkner, P. & Borkovec, M. Reaction-rate theory: fifty years after Kramers. Rev. Mod. Phys. 62, 251–341 (1990)
Acknowledgements
We thank E.R. Edwards for contributions towards the construction of the experiment. We acknowledge funding from AFOSR (MURI), ARO, and ARO (MURI). E.B.N. acknowledges funding from the NSF GRFP.
Author information
Authors and Affiliations
Contributions
All authors contributed to the experiment, the analysis of the results and the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
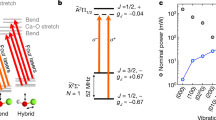
Extended Data Figure 1 Relevant energy levels and transitions in SrF.
a, Vibrational branching in SrF. Solid upward arrows denote transitions driven by the MOT lasers. Spontaneous decays from the A2Π1/2(v′ = 0) state (solid wavy arrows) and A2Π1/2(v′ = 1, 2) states (dashed wavy arrows) are governed by the vibrational branching fractions b0v, b1v and b2v, as shown. b, Optical addressing scheme for the SrF MOT. c, Energy levels of the X2Σ(v = 0, N = 1) state versus B. Energy levels are labelled by their mF value with mF = 2 (red lines), mF = 1 (orange lines), mF = 0 (green), mF = −1 (blue) and mF = −2 (purple).
Extended Data Figure 2 Slowing laser spectra.
a, Scale diagram showing the frequency extent of the  ,
,  and
and  slowing lasers (vertical red bars) relative to the four SR/HF manifolds of the X2Σ(v = 0, 1, 2; N = 1) states of SrF (horizontal black bars to right). The relative splittings of the four SR/HF levels in the X2Σ(N = 1) state are the same to within ∼1 MHz for v = 0, 1, 2 (ref. 31). The dashed lines mark the centres of the N = 1 SR/HF levels for the labelled velocity, and the level structure shown corresponds to v = 0 m s−1. b, Optimized spectral profiles of the three slowing lasers. The upper x axis shows velocity for a Doppler shift equivalent to the frequency labelled on the lower x axis. The
slowing lasers (vertical red bars) relative to the four SR/HF manifolds of the X2Σ(v = 0, 1, 2; N = 1) states of SrF (horizontal black bars to right). The relative splittings of the four SR/HF levels in the X2Σ(N = 1) state are the same to within ∼1 MHz for v = 0, 1, 2 (ref. 31). The dashed lines mark the centres of the N = 1 SR/HF levels for the labelled velocity, and the level structure shown corresponds to v = 0 m s−1. b, Optimized spectral profiles of the three slowing lasers. The upper x axis shows velocity for a Doppler shift equivalent to the frequency labelled on the lower x axis. The  light is modulated via a fibre EOM with fmod = 3.5 MHz. The
light is modulated via a fibre EOM with fmod = 3.5 MHz. The  and
and  lasers are each modulated by passing through two bulk EOMs with resonant frequencies at ∼40 MHz and ∼9 MHz.
lasers are each modulated by passing through two bulk EOMs with resonant frequencies at ∼40 MHz and ∼9 MHz.
Extended Data Figure 3 Molecular beam longitudinal velocity.
Shown are examples of slowed (grey circles) and unslowed (black squares) velocity profiles of the molecular beam detected upstream from the trapping region at  . These profiles are for the optimized slowing conditions that produce the largest MOT, as discussed in the main text.
. These profiles are for the optimized slowing conditions that produce the largest MOT, as discussed in the main text.
Extended Data Figure 4 MOT dependence on laser frequency.
Shown is LIF in the trapping region versus detuning when Δ00 and  are varied together (top), when
are varied together (top), when  is varied alone (middle) and when Δ10 is varied alone (bottom). As expected (and typically observed for atomic MOTs), the SrF MOT operates over a fairly narrow range of negative detuning values for the trapping lasers but requires only that the repump lasers be sufficiently near resonance. Error bars, standard error for multiple scans across each detuning range (14 scans for top and middle; 24 scans for bottom).
is varied alone (middle) and when Δ10 is varied alone (bottom). As expected (and typically observed for atomic MOTs), the SrF MOT operates over a fairly narrow range of negative detuning values for the trapping lasers but requires only that the repump lasers be sufficiently near resonance. Error bars, standard error for multiple scans across each detuning range (14 scans for top and middle; 24 scans for bottom).
Rights and permissions
About this article
Cite this article
Barry, J., McCarron, D., Norrgard, E. et al. Magneto-optical trapping of a diatomic molecule. Nature 512, 286–289 (2014). https://doi.org/10.1038/nature13634
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature13634
This article is cited by
-
Raman sideband cooling of molecules in an optical tweezer array
Nature Physics (2024)
-
Precision spectroscopy and laser-cooling scheme of a radium-containing molecule
Nature Physics (2024)
-
Probing site-resolved correlations in a spin system of ultracold molecules
Nature (2023)
-
Laser cooling of molecules
Journal of the Korean Physical Society (2023)
-
Evidence for the association of triatomic molecules in ultracold 23Na40K + 40K mixtures
Nature (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.