Abstract
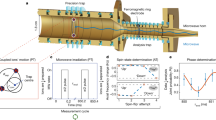
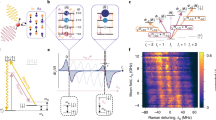
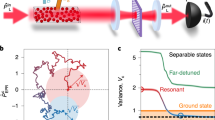
Electrons have an intrinsic, indivisible, magnetic dipole aligned with their internal angular momentum (spin). The magnetic interaction between two electronic spins can therefore impose a change in their orientation. Similar dipolar magnetic interactions exist between other spin systems and have been studied experimentally. Examples include the interaction between an electron and its nucleus and the interaction between several multi-electron spin complexes1,2,3,4,5. The challenge in observing such interactions for two electrons is twofold. First, at the atomic scale, where the coupling is relatively large, it is often dominated by the much larger Coulomb exchange counterpart1. Second, on scales that are substantially larger than the atomic, the magnetic coupling is very weak and can be well below the ambient magnetic noise. Here we report the measurement of the magnetic interaction between the two ground-state spin-1/2 valence electrons of two 88Sr+ ions, co-trapped in an electric Paul trap. We varied the ion separation, d, between 2.18 and 2.76 micrometres and measured the electrons’ weak, millihertz-scale, magnetic interaction as a function of distance, in the presence of magnetic noise that was six orders of magnitude larger than the magnetic fields the electrons apply on each other. The cooperative spin dynamics was kept coherent for 15 seconds, during which spin entanglement was generated, as verified by a negative measured value of −0.16 for the swap entanglement witness. The sensitivity necessary for this measurement was provided by restricting the spin evolution to a decoherence-free subspace that is immune to collective magnetic field noise. Our measurements show a d−3.0(4) distance dependence for the coupling, consistent with the inverse-cube law.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Budker D., Kimball D. F., DeMille D. P., eds. Atomic Physics: An Exploration through Problems and Solutions 1–50 (Oxford Univ. Press, 2004)
Stuhler, J. et al. Observation of dipole-dipole interaction in a degenerate quantum gas. Phys. Rev. Lett. 95, 150406 (2005)
Lu, M., Burdick, N. Q., Youn, S. H. & Lev, B. L. Strongly dipolar Bose-Einstein condensate of dysprosium. Phys. Rev. Lett. 107, 190401 (2011)
Dolde, F. et al. Room-temperature entanglement between single defect spins in diamond. Nature Phys. 9, 139–143 (2013)
Grinolds, M. S. et al. Nanoscale magnetic imaging of a single electron spin under ambient conditions. Nature Phys. 9, 215–219 (2013)
Rugar, D., Budakian, R., Mamin, H. & Chui, B. Single spin detection by magnetic resonance force microscopy. Nature 430, 329–332 (2004)
Hanneke, D., Fogwell, S. & Gabrielse, G. New measurement of the electron magnetic moment and the fine structure constant. Phys. Rev. Lett. 100, 120801 (2008)
Akerman, N., Glickman, Y., Kotler, S., Keselman, A. & Ozeri, R. Quantum control of 88Sr+ in a miniature linear Paul trap. Appl. Phys. B 107, 1167–1174 (2012)
Wineland, D. et al. Experimental issues in coherent quantum-state manipulation of trapped atomic ions. J. Res. Natl. Inst. Stand. Technol. 103, 259–328 (1998)
Roos, C. F., Chwalla, M., Kim, K., Riebe, M. & Blatt, R. ‘Designer atoms’ for quantum metrology. Nature 443, 316–319 (2006)
Turchette, Q. A. et al. Heating of trapped ions from the quantum ground state. Phys. Rev. A 61, 063418 (2000)
Biercuk, M. J., Uys, H., Britton, J. W., VanDevender, A. P. & Bollinger, J. J. Ultrasensitive detection of force and displacement using trapped ions. Nature Nanotechnol. 5, 646–650 (2010)
Roos, C. F. et al. Bell states of atoms with ultralong lifetimes and their tomographic state analysis. Phys. Rev. Lett. 92, 220402 (2004)
Langer, C. et al. Long-lived qubit memory using atomic ions. Phys. Rev. Lett. 95, 060502 (2005)
Kotler, S., Akerman, N., Glickman, Y., Keselman, A. & Ozeri, R. Single-ion quantum lock-in amplifier. Nature 473, 61–65 (2011)
Schmidt-Kaler, F. & Gerritsma, R. Entangled states of trapped ions allow measuring the magnetic field gradient produced by a single atomic spin. Europhys. Lett. 99, 53001 (2012)
Kotler, S., Akerman, N., Glickman, Y. & Ozeri, R. Nonlinear single-spin spectrum analyzer. Phys. Rev. Lett. 110, 110503 (2013)
Chou, C. W., Hume, D. B., Rosenband, T. & Wineland, D. J. Optical clocks and relativity. Science 329, 1630–1633 (2010)
Breit, G. The magnetic moment of the electron. Nature 122, 649 (1928)
Sackett, C. A. et al. Experimental entanglement of four particles. Nature 404, 256–259 (2000)
Navon, N. et al. Quantum process tomography of a Mølmer-Sørensen interaction. Preprint at http://arxiv.org/abs/1309.4502 (2013)
Horodecki, M., Horodecki, P. & Horodecki, R. Separability of mixed states: necessary and sufficient conditions. Phys. Lett. A 223, 1–8 (1996)
Moody, J. E. & Wilczek, F. New macroscopic forces? Phys. Rev. D 30, 130–138 (1984)
Ozeri, R. Heisenberg limited metrology using quantum error-correction codes. Preprint at http://arxiv.org/abs/1310.3432 (2013)
Arrad, G., Vinkler, Y., Aharonov, D. & Retzker, A. Increasing sensing resolution with error correction. Phys. Rev. Lett. 112, 150801 (2014)
Kessler, E. M. et al. Quantum error correction for metrology. Phys. Rev. Lett. 112, 150802 (2014)
Dür, W., Skotiniotis, M., Fröwis, F. & Kraus, B. Improved quantum metrology using quantum error correction. Phys. Rev. Lett. 112, 080801 (2014)
Keselman, A., Glickman, Y., Akerman, N., Kotler, S. & Ozeri, R. High-fidelity state detection and tomography of a single-ion Zeeman qubit. New J. Phys. 13, 073027 (2011)
Warring, U. et al. Individual-ion addressing with microwave field gradients. Phys. Rev. Lett. 110, 173002 (2013)
Navon, N. et al. Addressing two-level systems variably coupled to an oscillating field. Phys. Rev. Lett. 111, 073001 (2013)
Acknowledgements
We thank J. Avron for discussions on the entanglement witness. We acknowledge support by the Israeli Science Foundation, the Crown Photonics Center, the German-Israeli Science Foundation and M. Kushner Schnur, Mexico.
Author information
Authors and Affiliations
Contributions
S.K. designed the scheme for measuring spin–spin coupling. S.K. and N.A. performed the measurements. S.K. analysed the results. S.K., N.A., N.N. and Y.G. developed the techniques necessary to experimentally implement the measurement scheme. S.K. and R.O. wrote the paper. R.O. supervised the work. All authors discussed the results and contributed to the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
This file contains Supplementary Text and Data: (1) Details of the experimental setup, state preparation, detection and manipulation and also a discussion of motion heating;(2) Analytic derivation of magnetic spin-spin Hamiltonian evolution; (3) Analytic derivation of the parity and swap observables, taking preparation and detection fidelities into account, Allan deviation analysis of swap data and details of the Monte-Carlo swap error estimation; (4) Error analysis of adversary effects including motion heating, micromotion, quantization axis direction fluctuation, trap magnetic fields, spin-orbit coupling and mutually induced magnetic fields. (PDF 417 kb)
Rights and permissions
About this article
Cite this article
Kotler, S., Akerman, N., Navon, N. et al. Measurement of the magnetic interaction between two bound electrons of two separate ions. Nature 510, 376–380 (2014). https://doi.org/10.1038/nature13403
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature13403
This article is cited by
-
Breaking Landauer's bound in a spin-encoded quantum computer
Quantum Information Processing (2022)
-
Addressing Single Nuclear Spins Quantum Memories by a Central Electron Spin
Applied Magnetic Resonance (2022)
-
Single ion qubit with estimated coherence time exceeding one hour
Nature Communications (2021)
-
Double Electron–Electron Resonance Between Trapped Electron and Hole in a Semiconductor
Applied Magnetic Resonance (2018)
-
Atomic-scale sensing of the magnetic dipolar field from single atoms
Nature Nanotechnology (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.