Abstract
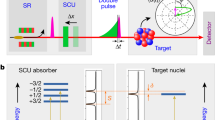
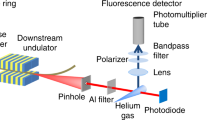
The concepts and ideas of coherent, nonlinear and quantum optics have been extended to photon energies in the range of 10–100 kiloelectronvolts, corresponding to soft γ-ray radiation (the term used when the radiation is produced in nuclear transitions) or, equivalently, hard X-ray radiation (the term used when the radiation is produced by electron motion). The recent experimental achievements in this energy range include the demonstration of parametric down-conversion in the Langevin regime1, electromagnetically induced transparency in a cavity2, the collective Lamb shift3, vacuum-assisted generation of atomic coherences4 and single-photon revival in nuclear absorbing multilayer structures5. Also, realization of single-photon coherent storage6 and stimulated Raman adiabatic passage7 were recently proposed in this regime. More related work is discussed in a recent review8. However, the number of tools for the coherent manipulation of interactions between γ-ray photons and nuclear ensembles remains limited. Here we suggest and implement an efficient method to control the waveforms of γ-ray photons coherently. In particular, we demonstrate the conversion of individual recoilless γ-ray photons into a coherent, ultrashort pulse train and into a double pulse. Our method is based on the resonant interaction of γ-ray photons with an ensemble of nuclei with a resonant transition frequency that is periodically modulated in time. The frequency modulation, which is achieved by a uniform vibration of the resonant absorber, owing to the Doppler effect, renders resonant absorption and dispersion both time dependent, allowing us to shape the waveforms of the incident γ-ray photons. We expect that this technique will lead to advances in the emerging fields of coherent and quantum γ-ray photon optics, providing a basis for the realization of γ-ray-photon/nuclear-ensemble interfaces and quantum interference effects at nuclear γ-ray transitions.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Shwartz, S. et al. X-ray parametric down-conversion in the Langevin regime. Phys. Rev. Lett. 109, 013602 (2012)
Röhlsberger, R., Wille, H.-C., Schlage, K. & Sahoo, B. Electromagnetically induced transparency with resonant nuclei in a cavity. Nature 482, 199–203 (2012)
Röhlsberger, R., Schlage, K., Sahoo, B., Couet, S. & Rüffer, R. Collective Lamb shift in single-photon superradiance. Science 328, 1248–1251 (2010)
Heeg, K. P. et al. Vacuum-assisted generation and control of atomic coherences at x-ray energies. Phys. Rev. Lett. 111, 073601 (2013)
Shakhmuratov, R., Vagizov, F. & Kocharovskaya, O. Single γ-photon revival and radiation burst in a sandwich absorber. Phys. Rev. A 87, 013807 (2013)
Liao, W.-T., Pálffy, A. & Keitel, C. H. Coherent storage and phase modulation of single hard-X-ray photons using nuclear excitons. Phys. Rev. Lett. 109, 197403 (2012)
Liao, W.-T., Pálffy, A. & Keitel, C. H. Nuclear coherent population transfer with X-ray laser pulses. Phys. Lett. B 705, 134–138 (2011)
Adams, B. W. et al. X-ray quantum optics. J. Mod. Opt. 60, 2–21 (2013)
Ma, X.-S. et al. Quantum teleportation over 143 kilometres using active feed-forward. Nature 489, 269–273 (2012)
Döring, F. et al. Sub-5 nm hard X-ray point focusing by a combined Kirkpatrick-Baez mirror and multilayer zone plate. Opt. Express 21, 19311–19323 (2013)
Hammerer, K., Sørensen, A. S. & Polzik, E. S. Quantum interface between light and atomic ensembles. Rev. Mod. Phys. 82, 1041–1093 (2010)
Hoy, G. R., Hamill, D. W. & Wintersteiner, P. P. in Mössbauer Effect Methodology Vol. 6 (ed. Gruverman, I. J. ) 109–121 (Plenum, 1970)
Amann, J. et al. Demonstration of self-seeding in a hard-X-ray free-electron laser. Nature Photon. 6, 693–698 (2012)
Shvyd’ko, Stoupin, S., Blank, V. & Terentyev, S. Near-100% Bragg reflectivity of X-rays. Nature Photon. 5, 539–542 (2011)
Antonov, V. A., Radeonychev, Y. V. & Kocharovskaya, O. Formation of a single attosecond pulse via interaction of resonant radiation with a strongly perturbed atomic transition. Phys. Rev. Lett. 110, 213903 (2013)
Helistö, P., Tittonen, I. & Katila, T. Enhanced transient effects due to saturated absorption of recoilless γ-radiation. Phys. Rev. B 34, 3458–3461 (1986)
Smirnov, G. V. & Potzel, W. Perturbation of nuclear excitons by ultrasound. Hyperfine Interact. 123/124, 633–663 (1999)
Kuznetsova, E., Kolesov, R. & Kocharovskaya, O. Compression of γ-ray photons into ultrashort pulses. Phys. Rev. A 68, 043825 (2003)
Smirnov, G. V. General properties of nuclear resonant scattering. Hyperfine Interact. 123/124, 31–77 (1999)
Kagan Theory of coherent phenomena and fundamentals in nuclear resonant scattering. Hyperfine Interact. 123/124, 83–126 (1999)
Hannon, J. P. & Trammell, G. T. Coherent gamma-ray optics. Hyperfine Interact. 123/124, 127–274 (1999)
Kolchin, P., Belthangady, C., Du, S., Yin, G. Y. & Harris, S. E. Electro-optic modulation of single photons. Phys. Rev. Lett. 101, 103601 (2008)
Pittman, T. It’s a good time for time-bin qubits. Physics 6, 110 (2013)
Röhlsberger, R. Nuclear Condensed Matter Physics using Synchrotron Radiation (Springer Tracts Mod. Phys. 208, Springer, 2005)
Radeonychev, Y. V., Tokman, M. D., Litvak, A. G. & Kocharovskaya, O. Acoustically induced transparency in optically dense resonance medium. Phys. Rev. Lett. 96, 093602 (2006)
Kocharovskaya, O. A. & Khanin, Ya. I. Population trapping and coherent bleaching of a three-level medium by a periodic train of ultrashort pulses. Sov. Phys. JETP 63, 945–949 (1986)
Harris, S. E. Electromagnetically induced transparency. Phys. Today 50, 36–42 (1997)
Fleischhauer, M., Imamoğlu, A. & Marangos, J. P. Electromagnetically induced transparency: optics in coherent media. Rev. Mod. Phys. 77, 633–673 (2005)
Lvovsky, A. I., Sanders, B. C. & Tittel, W. Optical quantum memory. Nature Photon. 3, 706–714 (2009)
Simon, C. et al. Quantum memories. Eur. Phys. J. D 58, 1–22 (2010)
Acknowledgements
We acknowledge the support from the US NSF (grant no. PHY-1307346), the RFBR (grants nos 13-02-00831 and 12-02-00263) and The Ministry of Education and Science of the Russian Federation (contract no. 11.G34.31.0011). V.A. acknowledges support from the Dynasty Foundation.
Author information
Authors and Affiliations
Contributions
F.V. developed the experimental methods, designed the experiment and derived all the experimental results. V.A., Y.V.R. and R.N.S. developed the theoretical description. V.A. and F.V. determined the optimal parameters for the experiments and provided the theoretical fit to experimental data. Y.V.R. and F.V. suggested the technique for observing the single-photon waveforms. R.N.S. obtained analytical solutions for some limiting cases. O.K. suggested the idea, coordinated the efforts and wrote the paper. All authors discussed the results and edited the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
Extended Data Figure 1 Time dependences of a γ-photon detection probability for different values of modulation index.
The values of modulation index are p = 0.8 (blue dashed line), p = 1.8 (red solid line) and p = 2.8 (green dashed line). All the other parameters are the same as in our experiment (Fig. 3).
Extended Data Figure 2 Time dependences of a γ-photon detection probability for different detunings of the central frequency of the source, ωr, from the resonance frequency of the absorber, ωa.
The values of detuning are ωr − ωa = 0.5Ω (blue dashed line), ωr − ωa = Ω (red solid line) and ωr − ωa = 2Ω (green dashed line). All the other parameters are the same as in our experiment (Fig. 3).
Extended Data Figure 3 Variation of the waveform of a 14.4-keV γ-photon with a change in the vibration phase, 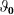 , at the moment of detection of the preceding 122-keV γ-photon.
, at the moment of detection of the preceding 122-keV γ-photon.
The parameter values are the same as in Fig. 3c, corresponding to double-pulse formation, except for the initial phases of vibration, which are as follows:  , the same as in Fig. 3c (red solid line),
, the same as in Fig. 3c (red solid line),  (blue dashed line),
(blue dashed line),  (the same as in the inset of Fig. 3c (green dashed line)) and
(the same as in the inset of Fig. 3c (green dashed line)) and  (cyan dashed line).
(cyan dashed line).
Extended Data Figure 5 Count rate of 14.4-keV photons versus time for the case of Fig. 4.
The blue dots centred at the confidence intervals correspond to the experimental data, and the red and green solid curves are plotted according to equations (13) and (14) and, respectively, equation (15).
Rights and permissions
About this article
Cite this article
Vagizov, F., Antonov, V., Radeonychev, Y. et al. Coherent control of the waveforms of recoilless γ-ray photons. Nature 508, 80–83 (2014). https://doi.org/10.1038/nature13018
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature13018
This article is cited by
-
Measurement of the sub-nanometer vibration amplitudes using 57Fe synchrotron Mössbauer source
Interactions (2024)
-
Optimal Motion Law of a Resonant Nuclear Absorber for the Formation of Short Pulses of Mössbauer Radiation
Radiophysics and Quantum Electronics (2023)
-
Slowing down x-ray photons in a vibrating recoilless resonant absorber
Scientific Reports (2022)
-
Reply to: On yoctosecond science
Nature (2022)
-
Nonlinearity-mediated digitization and amplification in electromechanical phonon-cavity systems
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

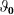 , at the moment of detection of the preceding 122-keV γ-photon.
, at the moment of detection of the preceding 122-keV γ-photon.