Abstract
Nucleation of aerosol particles from trace atmospheric vapours is thought to provide up to half of global cloud condensation nuclei1. Aerosols can cause a net cooling of climate by scattering sunlight and by leading to smaller but more numerous cloud droplets, which makes clouds brighter and extends their lifetimes2. Atmospheric aerosols derived from human activities are thought to have compensated for a large fraction of the warming caused by greenhouse gases2. However, despite its importance for climate, atmospheric nucleation is poorly understood. Recently, it has been shown that sulphuric acid and ammonia cannot explain particle formation rates observed in the lower atmosphere3. It is thought that amines may enhance nucleation4,5,6,7,8,9,10,11,12,13,14,15,16, but until now there has been no direct evidence for amine ternary nucleation under atmospheric conditions. Here we use the CLOUD (Cosmics Leaving OUtdoor Droplets) chamber at CERN and find that dimethylamine above three parts per trillion by volume can enhance particle formation rates more than 1,000-fold compared with ammonia, sufficient to account for the particle formation rates observed in the atmosphere. Molecular analysis of the clusters reveals that the faster nucleation is explained by a base-stabilization mechanism involving acid–amine pairs, which strongly decrease evaporation. The ion-induced contribution is generally small, reflecting the high stability of sulphuric acid–dimethylamine clusters and indicating that galactic cosmic rays exert only a small influence on their formation, except at low overall formation rates. Our experimental measurements are well reproduced by a dynamical model based on quantum chemical calculations of binding energies of molecular clusters, without any fitted parameters. These results show that, in regions of the atmosphere near amine sources, both amines and sulphur dioxide should be considered when assessing the impact of anthropogenic activities on particle formation.
Similar content being viewed by others
Main
The primary vapour responsible for atmospheric nucleation is thought to be sulphuric acid (H2SO4), derived from the oxidation of sulphur dioxide. However, peak daytime H2SO4 concentrations in the atmospheric boundary layer are about 106 to 3 × 107 cm−3 (0.04–1.2 parts per trillion by volume (p.p.t.v.)), which results in negligible binary homogeneous nucleation of H2SO4–H2O (ref. 3). Additional species such as ammonia or amines4,5 are therefore necessary to stabilize the embryonic clusters and decrease evaporation. However, ammonia cannot account for particle formation rates observed in the boundary layer3 and, despite numerous field and laboratory studies6,7,8,9,10,11,12,13,14,15,16, amine ternary nucleation has not yet been observed under atmospheric conditions. Amine emissions are dominated by anthropogenic activities (mainly animal husbandry), but about 30% of emissions are thought to arise from the breakdown of organic matter in the oceans, and 20% from biomass burning and soil8,17. Atmospheric measurements of gas-phase amines are sparse, but typical values range between negligible and a few tens of p.p.t.v. per amine species17,18,19,20.
Here we report results from the CLOUD experiment at CERN (for experimental details see Methods, Extended Data Fig. 1 and Supplementary Information). The data were obtained during three campaigns at the CERN Proton Synchrotron between October 2010 and November 2012, and comprise measurements of sulphuric acid–amine nucleation at atmospheric concentrations. Dimethylamine (DMA; C2H7N) was selected for this study because it is expected to have cluster binding energies representative of other light alkyl amines4.
Nucleation rates J were measured under neutral (Jn), galactic cosmic ray (Jgcr) and π+ beam (Jπ) conditions, corresponding to ion-pair concentrations of about 0, 650 and 3,000 cm−3, respectively. Both Jgcr and Jπ comprise the sum of neutral and ion-induced nucleation rates, whereas Jn measures the neutral rate alone. Figure 1 shows the nucleation rates at 1.7 nm mobility diameter (1.4 nm mass diameter) as a function of [H2SO4] for ‘binary’ (H2SO4–H2O), ammonia ternary (H2SO4–NH3–H2O) and amine ternary (H2SO4–DMA–H2O) nucleation at 278 K and 38% relative humidity (RH). Here ‘binary’ includes previous measurements made in the presence of NH3 and DMA contaminants3, estimated from later campaigns to be <2 p.p.t.v. and <0.1 p.p.t.v., respectively, for the conditions of ref. 3. Nucleation rates with 5 p.p.t.v. DMA are enhanced more than 1,000-fold compared with 250 p.p.t.v. ammonia (Fig. 1). Additional DMA up to 140 p.p.t.v. results in a less than threefold further rate increase, indicating that amine levels of about 5 p.p.t.v. are sufficient to reach the rate limit for amine ternary nucleation under atmospheric conditions ([H2SO4] ≤ 3 × 107 cm−3, or 1.2 p.p.t.v.).
Observations in the atmospheric boundary layer are indicated by small coloured squares21,22,23. The CLOUD data, recorded at 38% RH and 278 K, show Jgcr with only H2SO4, water and contaminants (<0.1 p.p.t.v. DMA and <2 p.p.t.v. NH3) in the chamber (open black circles, curve 1); Jgcr with <0.1 p.p.t.v. DMA and 2–250 p.p.t.v. NH3 (coloured triangles, curve 2); and Jn, Jgcr and Jπ with 10 p.p.t.v. NH3 and 3–5 p.p.t.v. DMA (coloured circles, curve 3), 5–13 p.p.t.v. DMA (coloured circles, curve 4) and 13–140 p.p.t.v. DMA (coloured circles, curve 5). The mixing ratios of NH3 or DMA are indicated by a colour scale. The curves are drawn to guide the eye; the straight sections follow power laws, J ∝ [H2SO4]n, with fitted slopes n of 3.6 ± 0.5 (curve 1), 2.7 ± 0.1 (curve 2), 5.0 ± 0.8 (curve 3), 3.6 ± 0.2 (curve 4) and 3.7 ± 0.1 (curve 5). The flattening of curves 1 and 2 at higher [H2SO4] results from saturation of the ion production rate and also a decreasing contribution of ammonia ternary nucleation. The bars indicate 1σ total errors, although the overall factor 2 systematic scale uncertainty on [H2SO4] is not shown. Theoretical expectations (ACDC model) are indicated for H2SO4 nucleation with 10 p.p.t.v. NH3 (dashed blue line and blue band) and for 10 p.p.t.v. DMA plus 10 p.p.t.v. NH3 (dashed red line and orange band, assuming a sticking probability of 0.5 for neutral–neutral collisions and 1.0 for charged–neutral collisions). The bands correspond to the uncertainty range of the theory: +1 and −1 kcal mol−1 binding energy (blue band) and sticking probabilities for neutral–neutral collisions between 0.1 and 1.0 (orange band), for the lower and upper limits, respectively.
The amine ternary nucleation rates pass through the band of atmospheric observations (Fig. 1). However, the latter reveal distinct regional differences, with some environments showing nucleation rates both above and below the amine limit (boreal forest and mountain21,22), whereas others are only below the limit (agricultural, livestock, industrial and urban21,23). This suggests that nucleation in different regions of the boundary layer may be controlled by different ternary vapours. In regions where amines are likely to be present (livestock farming and urban), the atmospheric rates are compatible with amine nucleation. However, the atmospheric data show considerable variability, probably resulting from variations in ternary vapour concentrations and particle coagulation sinks. When growth rates are low, the measured nucleation rates are highly sensitive to particle coagulation sinks, which influence particle losses both above and below the quoted formation threshold sizes. Losses below the threshold size are uncorrected, implying higher variability in the atmosphere, where conditions are less well defined than in the laboratory.
Figure 1 shows the theoretical expectations for NH3 (blue band) and DMA ternary nucleation (orange band), obtained with the Atmospheric Cluster Dynamics Code model (ACDC)24 (see Methods and Supplementary Information for further details). The model uses cluster evaporation and fragmentation rates calculated from quantum chemistry, with no fitted parameters25. The agreement is quite good, although the model predicts somewhat higher DMA ternary nucleation rates than measured experimentally. Part of this discrepancy is due to the smaller size—and hence higher formation rate—of the modelled clusters (up to four acid and four base molecules per cluster, corresponding to mobility diameters of 1.2–1.4 nm). Computational studies (see Supplementary Information and Extended Data Figs 2 and 3) indicate that DMA ternary nucleation is rather insensitive to RH or temperature, reflecting the strong acid–base binding. The experimental measurements obtained at 38% RH and 278 K may therefore be considered representative of a wide range of boundary layer conditions.
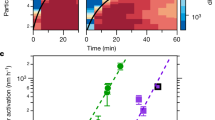
Plots of the nucleation rates Jn, Jgcr and Jπ against DMA mixing ratio are shown in Fig. 2a. Here, all measurements have been scaled to [H2SO4] = 2.0 × 106 cm−3 using the fitted slopes, n, from Fig. 1. The addition of only 5 p.p.t.v. DMA enhances the nucleation rate of sulphuric acid particles by more than six orders of magnitude, but the addition of further DMA up to 140 p.p.t.v. produces a negligible further increase. The measured neutral, galactic cosmic ray (GCR) and beam nucleation rates are indistinguishable, within experimental uncertainties. However, a more sensitive determination of the ion-induced nucleation rate,  , is obtained from direct ion measurements with the neutral cluster and air ion spectrometer. The ion-induced fractions, Jiin/Jgcr or Jiin/Jπ (Fig. 2b), are found to average about 20% at 0.5 cm−3 s−1 but grow in relative importance as the total nucleation rate decreases. This indicates that the influence of galactic cosmic rays on the nucleation of sulphuric acid–amine particles is only significant at low overall formation rates. No difference is measured for the ion-induced fraction under GCR or beam conditions (Fig. 2b). This follows, because the ion–ion recombination lifetimes are below 10 min and are comparable to the monomer arrival rate on the cluster (one molecule per 12 min for H2SO4·HSO4− at 106 cm−3 [H2SO4]). Consequently, although the ion pair concentration is larger for beam conditions, it is compensated for by a shorter ion lifetime, which decreases the time available for nucleation before the ion cluster is neutralized.
, is obtained from direct ion measurements with the neutral cluster and air ion spectrometer. The ion-induced fractions, Jiin/Jgcr or Jiin/Jπ (Fig. 2b), are found to average about 20% at 0.5 cm−3 s−1 but grow in relative importance as the total nucleation rate decreases. This indicates that the influence of galactic cosmic rays on the nucleation of sulphuric acid–amine particles is only significant at low overall formation rates. No difference is measured for the ion-induced fraction under GCR or beam conditions (Fig. 2b). This follows, because the ion–ion recombination lifetimes are below 10 min and are comparable to the monomer arrival rate on the cluster (one molecule per 12 min for H2SO4·HSO4− at 106 cm−3 [H2SO4]). Consequently, although the ion pair concentration is larger for beam conditions, it is compensated for by a shorter ion lifetime, which decreases the time available for nucleation before the ion cluster is neutralized.
Measurements recorded at 38% RH and 278 K. a, Nucleation rates, Jn, Jgcr and Jπ, as a function of DMA mixing ratio. b, Ion-induced fractions, Jiin/Jgcr and Jiin/Jπ, as a function of Jgcr or Jπ, at DMA = 3–140 p.p.t.v. In a, all nucleation rates are scaled to [H2SO4] = 2.0 × 106 cm−3 (0.08 p.p.t.v.) using the fitted slopes in Fig. 1. The point at 0.1 p.p.t.v. DMA shows the mean projected Jgcr measurement at contaminant-level DMA and NH3. The bars indicate 1σ total errors and include correlated systematic contributions. Theoretical expectations are shown by dashed red lines (sticking probability of 0.5 for neutral–neutral collisions and 1.0 for charged–neutral collisions) and uncertainties by orange bands (sticking probabilities for neutral–neutral collisions between 0.1 and 1.0).
Figure 3 shows the molecular composition of nucleating charged clusters in the presence of DMA for negative ions (Fig. 3a) and positive ions (Fig. 3b), measured with atmospheric-pressure interface time-of-flight mass spectrometers (APi-TOFs). The predominant negatively charged clusters include an HSO4− or HSO5− ion. The latter is deprotonated peroxysulphuric acid, whose presence varies with the ozone concentration in the chamber (it is absent when no ozone is present). We found no indication that the nucleation rates are sensitive to the relative contribution of these ion species. Contaminant NO3− ions are also detected, but at much lower concentrations. The predominant positively charged clusters contain a protonated DMA ion, DMA·H+ (C2H7N·H+), in association with H2SO4 and DMA. The remaining positive ions are largely protonated light organic contaminants, mostly also nitrogen-containing.
Molecular composition of charged clusters measured by the APi-TOF for Jgcr = 1.2 cm−3 s−1, 4.0 × 106 cm−3 [H2SO4], 11 p.p.t.v. NH3, 9.4 p.p.t.v. DMA, 38% RH and 278 K. a, Negative particles. b, Positive particles. Cluster mass/charge, m/z, defect (difference from integer m/z) is plotted against m/z; each circle represents a distinct molecular composition and its area represents counts s−1. The labels (n, m) indicate the number of sulphuric acid (nSA) and DMA (mDMA) molecules in pure clusters of SA and DMA, including both neutral and charged species. The addition of a single SA (H2SO4) or DMA (C2H7N) molecule to any cluster displaces it on the plot by a vector distance indicated by the grey arrows in b. Red circles represent pure SA clusters; green circles are clusters containing SA and DMA alone; black circles contain ammonia in addition (only appearing in some clusters above m/z = 900); other clusters (mostly containing light organic contaminants) are grey circles. Water molecules evaporate rapidly in the APi-TOF and are not detected (see Supplementary Information).
Amine ternary nucleation is observed to proceed by the same base-stabilization mechanism as that found previously for ammonia ternary nucleation3. We will use the label (n, m) to indicate the number of sulphuric acid (nSA) and DMA (mDMA) molecules in pure SA·DMA clusters, where n and m include both neutral and charged species. Negatively charged nucleation (Fig. 3a) proceeds as follows. The first step is dimer (2, 0) formation: HSO4−·H2SO4 (for simplicity the ‘HSO4−’ ion implies either HSO4− or HSO5−). This constitutes an acid–base pair because HSO4− is a Lewis base (an electron pair donor). Consequently the first negatively charged cluster to which DMA can bind to form an acid–base pair is the acid trimer. The most abundant acid trimer contains two DMA molecules (3, 2). Thereafter, each additional acid molecule is stabilized by one additional DMA molecule, following a sequence of acid–base pairs: (3, 2) → (4, 3) → (5, 4) → (n, n − 1). Our calculations suggest that the process involves mainly the accretion of SA·DMA (dimethylaminium bisulphate) clusters, but it may also involve the stepwise addition of an SA molecule followed by a DMA molecule. Beyond (7, 6) clusters, there is evidence for further neutralization of the acid by additional DMA (partial formation of dimethylaminium sulphate). Positively charged nucleation (Fig. 3b) proceeds similarly. Here DMA·H+ is a Lewis acid and so binds only weakly with H2SO4. Hence the first positively charged cluster is a DMA·H+ ion together with a single SA·DMA acid–base pair (1, 2). Thereafter, the cluster grows by the accretion of SA·DMA pairs, exactly as seen for negatively charged clusters. No DMA·H+ monomer is detected because its mass-to-charge ratio (m/z), 46, is below the APi-TOF cutoff, as configured for these experiments.
Because both HSO4− and DMA are Lewis bases, each can form an acid–base pair with H2SO4. In fact HSO4− is the stronger base, as demonstrated by its much stronger binding energy with H2SO4 (Supplementary Table 1)4. The only fundamental difference is that not more than one HSO4− ion can be present in the cluster because of electrostatic repulsion. So, although the APi-TOF measures only charged clusters in the CLOUD chamber, this suggests that neutral nucleation proceeds by the same mechanism, namely the initial formation of an acid–base pair (SA·DMA)—equivalent to the acid–base pair (SA·HSO4−) seen in charged nucleation (Fig. 3a)—and subsequently the accretion of additional SA·DMA pairs. This is also indicated by the Atmospheric Cluster Dynamics Code (ACDC) model (see Supplementary Information and Extended Data Fig. 4).
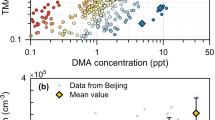
There is direct experimental evidence to support this picture of the neutral nucleation mechanism. Figure 4 shows a plot of the concentration of the neutral acid dimer against that of the neutral acid monomer, measured with the chemical ionization mass spectrometer (CIMS) before and after the addition of DMA, when the clearing field was present (implying that there were only neutral clusters in the CLOUD chamber). We infer from the observed absence of DMA on the negatively charged monomer or dimer (Fig. 3a) that, after charging in the CIMS, clusters containing one H2SO4 molecule will be detected as DMA-free charged monomers, and clusters containing two H2SO4 molecules will be detected as DMA-free charged dimers—regardless of whether or not they were originally clustered with DMA. Before adding any DMA, the dimer concentrations are consistent with the expected production in the CIMS ion source. However, with 5 p.p.t.v. DMA or more, the dimer concentrations are about six orders of magnitude higher than those expected for a pure binary system26. The concentration of neutral acid dimer with DMA approaches the kinetic limit, indicating highly stable clusters with negligible evaporation, and supporting the neutral nucleation mechanism inferred above.
Concentrations were measured by the CIMS in CLOUD without DMA (open circles) and with 3–140 p.p.t.v. DMA and 10 p.p.t.v. NH3 (coloured circles), at 38% RH and 278 K. Ions are absent from the CLOUD chamber (the clearing field is on). The bars indicate 1σ counting errors. The fitted red curve through the DMA data shows a quadratic dependence on monomer concentration. The other curves show the expected neutral dimer concentrations for the binary H2SO4–H2O system (short-dashed black line)26, for production in the CIMS ion source (dashed black line and grey uncertainty band) and for 10 p.p.t.v. DMA in the ACDC model, assuming 0.5 sticking probability (dashed red line). The orange band shows the model uncertainty range (sticking probabilities between 0.1 and 1.0). The brown curve indicates the upper limit of the dimer concentration calculated with the ACDC model, which is close to the kinetic limit (unit sticking probability and negligible evaporation).
A previous experiment27 measured unexpectedly high dimer concentrations in a laminar flow tube and concluded that a stabilizing contaminant must be present, although none was measured. This was proposed27 to explain the high ‘binary’ nucleation rates previously measured in ref. 28 in the same flow tube. Another experiment15 measured high dimer formation rates linked to amine mixing ratios of about 1 part per billion by volume and above. Our results directly link high concentrations of neutral H2SO4 dimer with amines at atmospheric levels.
The results reported here show that nucleation in the atmospheric boundary layer is highly sensitive to trace amine levels of only a few p.p.t.v. Sulphuric acid–amine nucleation is found to proceed by the same base-stabilization mechanism as that previously observed for ammonia, in which each additional acid molecule in the cluster is stabilized by one (or occasionally, two) base molecules3. However, the acid–base pairs that sulphuric acid forms with amines are more tightly bound than with ammonia, resulting in cluster formation rates that approach the kinetic limit. Little increase is seen above 5 p.p.t.v. DMA, indicating that nucleation at atmospheric H2SO4 concentrations (below 3 × 107 cm−3 or 1.2 p.p.t.v.) is then limited by the availability of H2SO4 and not that of DMA. Our experimental rate and molecular measurements are well reproduced by a dynamical model based on quantum chemical calculations of binding energies of molecular clusters.
Although measurements of ambient gas-phase amines are rare, mixing ratios of a few p.p.t.v. in the continental boundary layer have been reported17,19,20, suggesting that sulphuric acid–amine nucleation is likely to be an important atmospheric process. However, atmospheric observations indicate both the presence10,11,16 and the absence22 of a significant amine fraction in newly formed particles, which suggests considerable variability of ambient amine levels. Although amines are volatile vapours, our measurements show that sulphate particles constitute an almost perfect sink (negligible evaporation). However, unlike H2SO4, amine vapours are directly emitted from sources in their chemically active form and so they will be localized to source regions, with highly variable concentrations that depend on ambient sulphate particle sinks and OH radical levels (the DMA oxidation lifetime is about 4 h at 106 cm−3 [OH]). Amines can therefore explain only a part of atmospheric nucleation. Indeed, our measurements leave open the possibility that nucleation may also proceed with other atmospheric vapours, such as highly oxidized organic species of very low volatility. In such cases, extremely low amine concentrations may still enhance nucleation by forming stable acid–base pairs with some fraction of the sulphuric acid molecules in an embryonic cluster (constituting at least four-component nucleation).
The ion-induced contribution to amine ternary nucleation is generally small, except at low overall formation rates. Ions can enhance nucleation either by an increased collision rate between a charged cluster and polar molecules (such as H2SO4 or H2SO4·DMA) or by an increased cluster binding energy (and hence decreased evaporation rate). Because neutral clusters of H2SO4 and DMA are highly stable, charge offers little competitive advantage. Taken together with previous CLOUD measurements3, this suggests that ions can be significant in atmospheric particle formation provided that the associated neutral particles have appreciable evaporation and provided that the overall nucleation rates are low and below the ion-pair production rate.
The Intergovernmental Panel on Climate Change (IPCC) considers that the increased amount of aerosol in the atmosphere from human activities constitutes the largest present uncertainty in climate radiative forcing2 and projected climate change this century29. The results reported here show that the uncertainty is even greater than previously thought, because extremely low amine emissions—which have substantial anthropogenic sources and have not hitherto been considered by the IPCC—have a large influence on the nucleation of sulphuric acid particles. Moreover, amine scrubbing is likely to become the dominant technology for CO2 capture from fossil-fuelled power plants, so anthropogenic amine emissions are expected to increase in the future30. If amine emissions were to spread into pristine regions of the boundary layer where they could switch on nucleation, substantial increases in regional and global cloud condensation nuclei could occur. This underscores the importance of monitoring amine emissions—as well as those of sulphur dioxide—when assessing the impact of anthropogenic activities on the radiative forcing of regional and global climate by aerosols.
Methods Summary
CLOUD is designed to study the effects of cosmic rays on aerosols, cloud droplets and ice particles, under precisely controlled laboratory conditions. The CLOUD chamber and gas system have been built to the highest technical standards of cleanliness and performance. Owing to its large volume (26 m3) and highly stable operating conditions, the chamber allows nucleation rates to be measured reliably over a wide range from 0.001 cm−3 s−1 to well above 100 cm−3 s−1. The loss rate of condensable vapours onto the walls of the chamber is comparable to the condensation sink rate onto ambient aerosols under pristine atmospheric boundary layer conditions. The experiment has several unique aspects, including precise control of the ‘cosmic ray’ beam intensity from the CERN Proton Synchrotron, the capability to create an ion-free environment with an internal electric clearing field, precise and uniform adjustment of the H2SO4 concentration by means of ultraviolet illumination from a fibre-optic system, and highly stable operation at any temperature between 203 and 300 K. The contents of the chamber are continuously analysed by a suite of instruments connected to sampling probes that project into the chamber.
The experimental measurements are compared with theoretical expectations based on a dynamical model in which collision and coagulation rates are computed from kinetic gas theory. Equilibrium constants are computed from quantum chemical calculations of binding energies of molecular clusters, and evaporation and cluster fission rates are then obtained from detailed balance. All possible cluster–cluster processes are included. The electrostatic enhancement of ion–molecule collisions is calculated by using dipole moments and polarizabilities obtained from quantum chemistry. The model has no fitted parameters.
Online Methods
The key features of the CLOUD experiment (Extended Data Fig. 1) are a large-volume (26 m3) stainless steel chamber; precise (±0.01 K) temperature control at any tropospheric temperature; precise delivery of selected trace gases and ultra-pure humidified synthetic air; precise and uniform adjustment of the H2SO4 concentration by means of ultraviolet illumination from a fibre-optic system; suppression of contaminant vapours at the technological limit; an adjustable π+ beam from the CERN Proton Synchrotron to simulate cosmic rays; and the ability to simulate an ion-free environment by applying an electric field to sweep ions from the chamber.
A comprehensive array of state-of-the-art instruments continuously samples and analyses the contents of the chamber. For the results reported here, the instruments included a chemical ionization mass spectrometer for H2SO4 concentration31, two APi-TOFs (TOFWERK AG and Aerodyne Research, Inc.)32 for the molecular composition of positive and negative charged clusters, several condensation particle counters (CPCs) with 50% detection efficiency thresholds near 2 nm (two Airmodus A09 particle size magnifiers (PSMs)33, two diethylene glycol CPCs (DEG-CPCs)34,35, a TSI 3776 CPC and a TSI 3786 CPC), a scanning mobility particle sizer (SMPS), a neutral cluster and air ion spectrometer (NAIS)36, a proton transfer reaction time-of-flight mass spectrometer for organic vapours37, and an ion chromatograph for measurements of NH3 and DMA concentrations38.
Two particle counters were operated in a continuously stepped scanning mode to provide measurements of particle growth rates at small sizes: first, a PSM whose detection threshold was varied between about 1 and 2.5 nm, and second, the TSI 3786 with a variable laminar flow rate through its sampling probe, leading to a cutoff size between about 2.5 and 5 nm. The H2SO4 concentration is derived from channels 97 (HSO4−) and 160 (HNO3·HSO4−) of the CIMS, which measure the sulphuric acid monomer signal after charging in the CIMS ion source. The sulphuric acid dimer concentration measured by the CIMS is derived assuming the same calibration factor as for monomers.
Nucleation rates Jn, Jgcr and Jπ (cm−3 s−1) were measured as follows. Neutral nucleation rates are measured with no pion beam and with the field cage electrodes set to ±30 kV, which establishes an electric field of about 20 kV m−1 in the chamber. This completely suppresses ion-induced nucleation because, under these conditions, small ions or molecular clusters are swept from the chamber in about 1 s. Because all of the nucleation processes under consideration take place on substantially longer time scales, neutral nucleation rates can be measured with zero background from ion-induced nucleation. For GCR and beam conditions, the electric field was set to zero, leading to ion pair concentrations of about 650 −3 for Jgcr, representative of the boundary layer, and about 3,000 cm−3 for Jπ, representative of the top of the troposphere. Both Jgcr and Jπ comprise the sum of neutral and ion-induced nucleation rates, at their respective ion concentrations, whereas Jn measures the neutral rate alone.
The nucleation rates are obtained from the formation rates,  (where the subscript dth refers to the detection threshold diameter of the particle counter). The nucleation rates, J1.7, are determined at 1.7 nm mobility diameter (1.4 nm mass diameter) after correcting for losses between 1.7 nm and the detection size threshold39,40. A diameter of 1.7 nm corresponds to a cluster considered to be above the critical size and therefore thermodynamically stable. The critical size, which corresponds to equal evaporation and growth rates of the cluster, varies with temperature, chemical species and concentrations, and may even be absent when evaporation rates are highly suppressed as in the case of sulphuric acid–DMA clusters. Because the loss rate of freshly nucleated particles to the chamber walls is comparable to the rate at which they are lost in the atmosphere to pre-existing aerosols under pristine boundary-layer conditions, the reported formation rates at 1.7 nm size should correspond reasonably well to atmospheric observations of new particle formation.
(where the subscript dth refers to the detection threshold diameter of the particle counter). The nucleation rates, J1.7, are determined at 1.7 nm mobility diameter (1.4 nm mass diameter) after correcting for losses between 1.7 nm and the detection size threshold39,40. A diameter of 1.7 nm corresponds to a cluster considered to be above the critical size and therefore thermodynamically stable. The critical size, which corresponds to equal evaporation and growth rates of the cluster, varies with temperature, chemical species and concentrations, and may even be absent when evaporation rates are highly suppressed as in the case of sulphuric acid–DMA clusters. Because the loss rate of freshly nucleated particles to the chamber walls is comparable to the rate at which they are lost in the atmosphere to pre-existing aerosols under pristine boundary-layer conditions, the reported formation rates at 1.7 nm size should correspond reasonably well to atmospheric observations of new particle formation.
Before J1.7 is calculated, the measured particle number concentrations versus time are corrected39,40 in two sequential steps for the loss of particles due to the chamber walls, dilution and coagulation: first, particle losses above dth, and second, particle losses during growth from 1.7 nm to dth. The wall loss rate is 1.7 × 10−3 s−1 for H2SO4 monomers and decreases with increasing cluster diameter as 1/d. The dilution lifetime is 3–5 h, depending on the total sampling rate of all instruments attached to the chamber. Correction 2 above requires knowledge of the particle growth rate. This is determined experimentally from the different rise times measured in a scanning PSM, which detects particles over a range of threshold diameters between 1 and 2.5 nm. The growth rates were verified with several other instruments, including a fixed-threshold PSM, two DEG-CPCs, a TSI 3776, two APi-TOFs, a NAIS and a SMPS. Because instrumentally determined growth rates were not available for all runs, a parameterization was derived to allow the growth rate to be calculated for every run.
The detection thresholds of the particle counters do not represent perfect step functions, so particles with smaller diameters are detected to some extent. This leads to over-counting, which becomes a more important—and more uncertain—correction as the CPC threshold approaches 1.7 nm. For this reason, the nucleation rates reported here are based on a TSI 3776 CPC with dth = 3.2 nm since—although requiring the largest corrections for losses between 1.7 nm and the detection threshold—it has negligible sensitivity to clusters below 1.7 nm. To confirm the nucleation rates obtained with the 3.2 nm CPC, they were derived independently from the other CPCs with lower detection thresholds and verified to agree within systematic uncertainties.
The ion-induced nucleation rate, Jiin, for positive and negative particles is measured with the NAIS. This provides the most sensitive determination of the ion-induced fraction, Jiin/Jtotal, because the NAIS measures only charged clusters. Loss corrections are applied to the charged cluster spectra to account for wall losses, dilution and ion–ion recombination. In addition a source correction is applied to account for diffusion charging of neutral clusters by small ions. The latter correction requires knowledge of the number concentrations of small ions and of neutral clusters versus particle diameter. The neutral cluster concentrations are measured with the 3.2 nm TSI 3776 CPC and their size spectra are measured with the SMPS. The small-ion concentrations are measured with the AIS+ and AIS−. The charging (collision) probabilities are determined using the collision kernels versus diameter from ref. 41.
The error on J1.7 has three components that are added together in quadrature to estimate the total error indicated in Figs 1 and 2a. The first is a statistical measurement error derived from the scatter of the particle counter measurements, evaluated separately for each nucleation event; the second is an estimated +50%/−33% uncertainty on the calculated correction factor,  , where
, where  is the nucleation rate at size dth, obtained after correcting
is the nucleation rate at size dth, obtained after correcting  for detection losses. The third is a ±30% systematic uncertainty on
for detection losses. The third is a ±30% systematic uncertainty on  estimated from the run-to-run reproducibility of
estimated from the run-to-run reproducibility of  under nominally identical chamber conditions.
under nominally identical chamber conditions.
The error on Jiin has two main components. The first is a statistical measurement error derived from the scatter of the NAIS measurements, evaluated separately for each nucleation event. The second is an estimated ±50% error to account for the uncertainty in the correction for diffusion charging of neutral clusters by small ions. These errors are added together in quadrature with the error on J1.7 to estimate the error on the ion-induced fraction, Jiin/J1.7, shown in Fig. 2b.
The overall experimental uncertainty on [H2SO4] measured by the CIMS is estimated to be +100%/−50%, on the basis of three independent measurements: particle growth rate under binary nucleation conditions, the depletion rate of [SO2] by photo-oxidation, and an external calibration source42. However, the run-to-run relative experimental uncertainty on [H2SO4] is smaller, typically ±10%. In deriving the sulphuric acid dimer concentrations measured by the CIMS (Fig. 4), we assumed the same charging efficiency by the ion source as for monomers. The concentrations of SO2 and O3 are measured with calibrated instruments and are known to ±10%. The overall uncertainty on the NH3 mixing ratio is estimated to be +100%/−50%. The point-to-point uncertainty on the DMA mixing ratio is estimated to be ±(11% + 12%/[DMA] (p.p.t.v.)), with an overall scale uncertainty of +50%/−33%. The minimum directly measurable values are 2 p.p.t.v. for NH3 and 0.2 p.p.t.v. for DMA. However, lower values can be estimated from precise calibration of the trace gas delivery systems together with molecular analysis of the nucleating clusters in the APi-TOFs.
To compare the CLOUD measurements with theoretical expectations, all possible collision, coagulation, evaporation and fragmentation reactions have been explicitly simulated for a certain set of clusters. Collision and coagulation rates are computed from kinetic gas theory, while evaporation and fragmentation rates are obtained from quantum chemistry25. Dynamical simulations were performed with the ACDC model24 to calculate the formation of neutral, positively charged and negatively charged clusters containing sulphuric acid, ammonia and DMA. The electrostatic enhancement of ion–molecule collisions is calculated using dipole moments and polarizabilities obtained from quantum chemistry. The model has no fitted parameters. As a result of computing limitations, the formation and evaporation of clusters containing up to four sulphuric acid and four base molecules (mobility diameters 1.2–1.4 nm) have been modelled so far. The diameters of the largest computed clusters are smaller than the 1.7 nm size at which the experimental formation rates (J1.7) are determined. The modelled formation rates can therefore be expected to overestimate the CLOUD measurements somewhat. Further description of the ACDC model is provided in Supplementary Information.
References
Merikanto, J., Spracklen, D. V., Mann, G. W., Pickering, S. J. & Carslaw, K. S. Impact of nucleation on global CCN. Atmos. Chem. Phys. 9, 8601–8616 (2009)
IPCC. Climate Change 2007: the Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change (Cambridge Univ. Press, 2007)
Kirkby, J. et al. Role of sulphuric acid, ammonia and galactic cosmic rays in atmospheric aerosol nucleation. Nature 476, 429–433 (2011)
Kurtén, T., Loukonen, V., Vehkamäki, H. & Kulmala, M. Amines are likely to enhance neutral and ion-induced sulphuric acid-water nucleation in the atmosphere more effectively than ammonia. Atmos. Chem. Phys. 8, 4095–4103 (2008)
Loukonen, V. et al. Enhancing effect of dimethylamine in sulphuric acid nucleation in the presence of water—a computational study. Atmos. Chem. Phys. 10, 4961–4974 (2010)
Mäkelä, J. M. et al. Chemical composition of aerosol during particle formation events in boreal forest. Tellus 53B, 380–393 (2001)
Murphy, S. M. et al. Secondary aerosol formation from atmospheric reactions of aliphatic amines. Atmos. Chem. Phys. 7, 2313–2337 (2007)
Facchini, M. C. et al. Important source of marine secondary organic aerosol from biogenic amines. Environ. Sci. Technol. 42, 9116–9121 (2008)
Berndt, T. et al. Laboratory study on new particle formation from the reaction OH + SO2: influence of experimental conditions, H2O vapour, NH3 and the amine tert-butylamine on the overall process. Atmos. Chem. Phys. 10, 7101–7116 (2010)
Smith, J. N. et al. Observations of aminium salts in atmospheric nanoparticles and possible climatic implications. Proc. Natl Acad. Sci. USA 107, 6634–6639 (2010)
Zhao, J. et al. Observation of neutral sulphuric acid-amine containing clusters in laboratory and ambient measurements. Atmos. Chem. Phys. 11, 10,823–10,836 (2011)
Erupe, M. E., Viggiano, A. A. & Lee, S.-H. The effect of trimethylamine on atmospheric nucleation involving H2SO4 . Atmos. Chem. Phys. 11, 4767–4775 (2011)
Yu, H., McGraw, R. & Lee, S.-H. Effects of amines on formation of sub-3 nm particles and their subsequent growth. Geophys. Res. Lett. 39, L02807 (2012)
Zollner, J. H. et al. sulphuric acid nucleation: power dependencies, variation with relative humidity, and effect of bases. Atmos. Chem. Phys. 12, 4399–4411 (2012)
Chen, M. et al. Acid–base chemical reaction model for nucleation rates in the polluted atmospheric boundary layer. Proc. Natl Acad. Sci. USA 109, 18713–18718 (2012)
Creamean, J. M. et al. Measurements of aerosol chemistry during new particle formation events at a remote rural mountain site. Environ. Sci. Technol. 45, 8208–8216 (2011)
Ge, X., Wexler, A. S. & Clegg, S. L. Atmospheric amines—Part I. A review. Atmos. Environ. 45, 524–546 (2011)
Grönberg, L., Lövkvist, P. & Jönsson, J. A. Measurement of aliphatic-amines in ambient air and rainwater. Chemosphere 24, 1533–1540 (1992)
Hanson, D. R., McMurry, P. H., Jiang, J., Tanner, D. & Huey, L. G. Ambient pressure proton transfer mass spectrometry: detection of amines and ammonia. Environ. Sci. Technol. 45, 8881–8888 (2011)
Yu, H. & Lee, S.-H. Chemical ionisation mass spectrometry for the measurement of atmospheric amines. Environ. Chem. 9, 190–201 (2012)
Paasonen, P. et al. On the roles of sulphuric acid and low-volatility organic vapours in the initial steps of atmospheric new particle formation. Atmos. Chem. Phys. 10, 11223–11242 (2010)
Kulmala, M. et al. Direct observations of atmospheric aerosol nucleation. Science 339, 943–946 (2013)
Kuang, C., McMurry, P. H., McCormick, A. V. & Eisele, F. L. Dependence of nucleation rates on sulphuric acid vapour concentration in diverse atmospheric locations. J. Geophys. Res. 113, D10209 10.1029/2007JD009253. (2008)
McGrath, M. J. et al. Atmospheric Cluster Dynamics Code: a flexible method for solution of the birth-death equations. Atmos. Chem. Phys. 12, 2345–2355 (2012)
Ortega, I. K. et al. From quantum chemical formation free energies to evaporation rates. Atmos. Chem. Phys. 12, 225–235 (2012)
Hanson, D. R. & Lovejoy, E. R. Measurement of the thermodynamics of the hydrated dimer and trimer of sulphuric acid. J. Phys. Chem. A 110, 9525–9528 (2006)
Petäjä, T. et al. Experimental observation of strongly bound dimers of sulphuric acid: application to nucleation in the atmosphere. Phys. Rev. Lett. 106, 228302 (2011)
Sipilä, M. et al. The role of sulphuric acid in atmospheric nucleation. Science 327, 1243–1246 (2010)
Andreae, M. O., Jones, C. D. & Cox, P. M. Strong present-day aerosol cooling implies a hot future. Nature 435, 1187–1190 (2005)
Nielsen, C. J., Herrmann, H. & Weller, C. Atmospheric chemistry and environmental impact of the use of amines in carbon capture and storage (CCS). Chem. Soc. Rev. 41, 6684–6704 (2012)
Kürten, A., Rondo, L., Ehrhart, S. & Curtius, J. Performance of a corona ion source for measurement of sulphuric acid by chemical ionisation mass spectrometry. Atmos. Meas. Tech. 4, 437–443 (2011)
Junninen, H. et al. A high-resolution mass spectrometer to measure atmospheric ion composition. Atmos. Meas. Tech. 3, 1039–1053 (2010)
Vanhanen, J. et al. Particle size magnifier for nano-CN detection. Aerosol Sci. Technol. 45, 533–542 (2011)
Iida, K., Stolzenburg, M. R. & McMurry, P. H. Effect of working fluid on sub-2 nm particle detection with a laminar flow ultrafine condensation particle counter. Aerosol Sci. Technol. 43, 81–96 (2009)
Wimmer, D. et al. Performance of diethylene glycol based particle counters in the sub 3 nm size range. Atmos. Meas. Tech. Discuss. 6, 2151–2181 (2013)
Kulmala, M. et al. Towards direct measurement of atmospheric nucleation. Science 318, 89–92 (2007)
Graus, M., Müller, M. & Hansel, A. High resolution PTR-TOF: quantification and formula confirmation of VOC in real time. J. Am. Soc. Mass Spectrom. 21, 1037–1044 (2010)
Praplan, A. P., Bianchi, F., Dommen, J. & Baltensperger, U. Dimethylamine and ammonia measurements with ion chromatography during the CLOUD4 campaign. Atmos. Meas. Tech. 5, 2161–2167 (2012)
Kerminen, V.-M. & Kulmala, M. Analytical formulae connecting the ‘real’ and the ‘apparent’ nucleation rate and the nuclei number concentration for atmospheric nucleation events. J. Aerosol Sci. 33, 609–622 (2002)
Kulmala, M. & Kerminen, V.-M. On the formation and growth of atmospheric nanoparticles. Atmos. Res. 90, 132–150 (2008)
Laakso, L. et al. Kinetic nucleation and ions in boreal forest particle formation events. Atmos. Chem. Phys. 4, 2353–2366 (2004)
Kürten, A., Rondo, L., Ehrhart, S. & Curtius, J. Calibration of a chemical ionization mass spectrometer for the measurement of gaseous sulphuric acid. J. Phys. Chem. A 116, 6375–6386 (2012)
Acknowledgements
We thank J.-L. Agostini, P. Carrie, L.-P. De Menezes, F. Josa, I. Krasin, R. Kristic, O.S. Maksumov, S.V. Mizin, R. Sitals, A. Wasem and M. Wilhelmsson for their contributions to the experiment, and D. Hanson and P. McMurry for discussions on their unpublished measurements of ambient gas-phase amines. We thank the CSC Centre for Scientific Computing in Espoo, Finland, for computer time, and J. Pierce and P. Paasonen for discussions. We thank CERN for supporting CLOUD with technical and financial resources, and for providing a particle beam from the CERN Proton Synchrotron. This research received funding from the EC Seventh Framework Programme (Marie Curie Initial Training Network ‘CLOUD-ITN’ no. 215072, MC-ITN ‘CLOUD-TRAIN’ no. 316662, ERC-Starting ‘MOCAPAF’ grant 57360 and ERC-Advanced ‘ATMNUCLE’ grant 227463), the German Federal Ministry of Education and Research (projects 01LK0902A and 01LK1222A), the Swiss National Science Foundation (projects 200020_135307 and 206620_130527), the Academy of Finland (Center of Excellence project 1118615), the Academy of Finland (135054, 133872, 251427, 139656, 139995, 137749, 141217 and 141451), the Finnish Funding Agency for Technology and Innovation, the Väisälä Foundation, the Nessling Foundation, the Austrian Science Fund (FWF; projects P19546 and L593), the Portuguese Foundation for Science and Technology (project CERN/FP/116387/2010), the Swedish Research Council, Vetenskapsrådet (grant 2011-5120), the Presidium of the Russian Academy of Sciences and Russian Foundation for Basic Research (grants 08-02-91006-CERN and 12-02-91522-CERN), and the US National Science Foundation (grants AGS1136479 and CHE1012293).
Author information
Authors and Affiliations
Contributions
J.A. performed nucleation rate analysis. S.S. conducted APi-TOF charged-cluster analysis. A.Kü. performed CIMS neutral cluster analysis. O.K.-M. and I.O. were responsible for ACDC analysis and for ACDC Supplementary Information text. A.A., J.A., A.A., F.B., M.B., J.Do., A.Do., E.D., J.Du., S.E., A.F., J.H., M.H., T.J., H.J., M.K., H.K., J.K., J.Ka., A.Kü., A.Ku., A.N.K., K.L., M.L., V.M., S.M., T.N., T.P., A.P., F.R., L.R., M.R., N.S., R.S., S.S., M.Sim., M.Sip., A.T., J.T., G.T., A.V., C.W., D.W. and P.Y. conducted data collection and analysis. K.S.C., E.D., S.E., H.H., O.K.-M., T.K., J.L., V.L., M.M., T.O., I.O., I.R., H.V. and T.Y. performed modelling. J.K. wrote the manuscript. J.A., U.B., K.S.C., J.C., N.D., R.F., J.K., A.Kü, M.K., T.K., J.H.S., H.V. and D.R.W. interpreted the data and edited the manuscript. All authors contributed to development of the CLOUD facility and analysis instruments, and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
Extended Data Figure 2 Theoretical dependence of amine ternary nucleation rates on RH.
Modelled neutral nucleation rates as a function of RH (left-hand scale) at 2.0 × 106 cm−3 [H2SO4] and 278 K, and either 0.1 p.p.t.v. DMA (purple curve) or 10 p.p.t.v. DMA (red curve). The nucleation rates relative to their value at 38% RH are shown on the right-hand scale (dashed purple and red curves).
Extended Data Figure 3 Theoretical dependence of ammonia ternary and amine ternary nucleation rates on temperature.
Modelled GCR nucleation rates as a function of temperature (left-hand scale) at 2.0 × 106 cm−3 [H2SO4] and either 2.0 × 108 cm−3 [NH3] (blue curve) or 2.0 × 108 cm−3 [DMA] (red curve). (A concentration of 2.0 × 108 cm−3 is equivalent to mixing ratios between 7.0 p.p.t.v. at 255 K and 8.2 p.p.t.v. at 300 K.) The sulphuric acid–DMA nucleation rate relative to the value at T = 278 K is shown on the right-hand scale (dashed red line). In the sulphuric acid–DMA system a sticking probability of 0.5 is assumed for all neutral–neutral collisions, and 1.0 for all charged–neutral collisions.
Extended Data Figure 4 Theoretical concentrations of negative, positive and neutral clusters during DMA ternary nucleation.
Modelled steady-state concentrations (mDMA versus nSA) at 4.0 × 106 cm−3 [H2SO4], 10 p.p.t.v. DMA, 4 ion pairs cm−3 s−1 and 278 K. a, Negative clusters. b, Positive clusters. c, Neutral clusters. A sticking probability of 0.5 is assumed for all neutral–neutral collisions and 1.0 for all charged–neutral collisions. The numbers below the centre of each circle show log10C, where C (cm−3) is the cluster concentration (the threshold is 0.01 cm−3). The circle areas within each panel are proportional to C (with the exception of the DMA monomer in c).
Supplementary information
Supplementary Information
This file contains Supplementary Text and Data, Supplementary References and Supplementary Tables 1-6. (PDF 280 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution-Non-Commercial-ShareAlike 3.0 Unported licence. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-sa/3.0/.
About this article
Cite this article
Almeida, J., Schobesberger, S., Kürten, A. et al. Molecular understanding of sulphuric acid–amine particle nucleation in the atmosphere. Nature 502, 359–363 (2013). https://doi.org/10.1038/nature12663
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature12663
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.