Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Observation of quantum state collapse and revival due to the single-photon Kerr effect

Nature volume 495, pages 205–209 (2013)Cite this article

Subjects

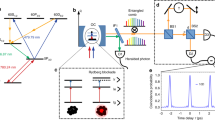
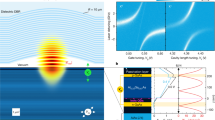
Abstract

To create and manipulate non-classical states of light for quantum information protocols, a strong, nonlinear interaction at the single-photon level is required. One approach to the generation of suitable interactions is to couple photons to atoms, as in the strong coupling regime of cavity quantum electrodynamic systems1,2. In these systems, however, the quantum state of the light is only indirectly controlled by manipulating the atoms3. A direct photon–photon interaction occurs in so-called Kerr media, which typically induce only weak nonlinearity at the cost of significant loss. So far, it has not been possible to reach the single-photon Kerr regime, in which the interaction strength between individual photons exceeds the loss rate. Here, using a three-dimensional circuit quantum electrodynamic architecture4, we engineer an artificial Kerr medium that enters this regime and allows the observation of new quantum effects. We realize a gedanken experiment5 in which the collapse and revival of a coherent state can be observed. This time evolution is a consequence of the quantization of the light field in the cavity and the nonlinear interaction between individual photons. During the evolution, non-classical superpositions of coherent states (that is, multi-component ‘Schrödinger cat’ states) are formed. We visualize this evolution by measuring the Husimi Q function and confirm the non-classical properties of these transient states by cavity state tomography. The ability to create and manipulate superpositions of coherent states in such a high-quality-factor photon mode opens perspectives for combining the physics of continuous variables6 with superconducting circuits. The single-photon Kerr effect could be used in quantum non-demolition measurement of photons7, single-photon generation8, autonomous quantum feedback schemes9 and quantum logic operations10.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Device layout and energy level diagram of the two-cavity, one-qubit device.
Figure 2: Technique for measuring the generalized Husimi Q functions.
Figure 3: Time evolution of Q 0 for a coherent state in the nonlinear cavity.
Figure 4: Wigner function of the multi-component cat states emerging during the Kerr interaction.

Similar content being viewed by others

References

  1. Wallraff, A. et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 431, 162–167 (2004)

    Article  CAS  ADS  Google Scholar 

  2. Haroche, S. & Raimond, J. M. Exploring the Quantum: Atoms, Cavities, And Photons (Oxford Univ. Press, 2006)

    Book  Google Scholar 

  3. Hofheinz, M. et al. Synthesizing arbitrary quantum states in a superconducting resonator. Nature 459, 546–549 (2009)

    Article  CAS  ADS  Google Scholar 

  4. Paik, H. et al. Observation of high coherence in Josephson junction qubits measured in a three-dimensional circuit QED architecture. Phys. Rev. Lett. 107, 240501 (2011)

    Article  ADS  Google Scholar 

  5. Yurke, B. & Stoler, D. The dynamic generation of Schrodinger cats and their detection. Physica B+C 151, 298–301 (1988)

    Article  ADS  Google Scholar 

  6. Braunstein, S. L. Quantum information with continuous variables. Rev. Mod. Phys. 77, 513–577 (2005)

    Article  ADS  MathSciNet  Google Scholar 

  7. Grangier, P., Levenson, J. & Poizat, J. Quantum non-demolition measurements in optics. Nature 396, 537–542 (1998)

    Article  CAS  ADS  Google Scholar 

  8. Peyronel, T. et al. Quantum nonlinear optics with single photons enabled by strongly interacting atoms. Nature 488, 57–60 (2012)

    Article  CAS  ADS  Google Scholar 

  9. Kerckhoff, J., Nurdin, H., Pavlichin, D. S. & Mabuchi, H. Designing quantum memories with embedded control: photonic circuits for autonomous quantum error correction. Phys. Rev. Lett. 105, 040502 (2010)

    Article  ADS  Google Scholar 

  10. Milburn, G. Quantum optical Fredkin gate. Phys. Rev. Lett. 62, 2124–2127 (1989)

    Article  CAS  ADS  Google Scholar 

  11. Saleh, B. E. A. & Teich, M. C. Fundamentals of Photonics (Wiley Series in Pure and Applied Optics, 1991)

    Book  Google Scholar 

  12. Slusher, R. E., Hollberg, L., Yurke, B., Mertz, J. & Valley, J. Observation of squeezed states generated by four-wave mixing in an optical cavity. Phys. Rev. Lett. 55, 2409–2412 (1985)

    Article  CAS  ADS  Google Scholar 

  13. Franken, P., Hill, A., Peters, C. & Weinreich, G. Generation of optical harmonics. Phys. Rev. Lett. 7, 118–119 (1961)

    Article  ADS  Google Scholar 

  14. Fisher, R. A., Kelley, P. L. & Gustafson, T. K. Subpicosecond pulse generation using the optical Kerr effect. Appl. Phys. Lett. 14, 140–143 (1969)

    Article  ADS  Google Scholar 

  15. Nigg, S. E. et al. Black-box superconducting circuit quantization. Phys. Rev. Lett. 108, 240502 (2012)

    Article  ADS  Google Scholar 

  16. Bourassa, J., Beaudoin, F., Gambetta, J. M. & Blais, A. Josephson-junction-embedded transmissionline resonators: from Kerr medium to in-line transmon. Phys. Rev. A 86, 013814 (2012)

    Article  ADS  Google Scholar 

  17. Bergeal, N. et al. Phase-preserving amplification near the quantum limit with a Josephson ring modulator. Nature 465, 64–68 (2010)

    Article  CAS  ADS  Google Scholar 

  18. Yurke, B. et al. Observation of 4.2-K equilibrium-noise squeezing via a Josephson-parametric amplifier. Phys. Rev. Lett. 60, 764–767 (1988)

    Article  CAS  ADS  Google Scholar 

  19. Yin, Y. et al. Dynamic quantum Kerr effect in circuit quantum electrodynamics. Phys. Rev. A 85, 023826 (2012)

    Article  ADS  Google Scholar 

  20. Hoffman, A. et al. Dispersive photon blockade in a superconducting circuit. Phys. Rev. Lett. 107, 053602 (2011)

    Article  CAS  ADS  Google Scholar 

  21. Shalibo, Y. et al. Direct Wigner tomography of a superconducting anharmonic oscillator. Preprint at http://arXiv.org/abs/1208.2441 (2012)

  22. Meekhof, D. M., Monroe, C., King, B. E., Itano, W. M. & Wineland, D. J. Generation of nonclassical motional states of a trapped atom. Phys. Rev. Lett. 76, 1796–1799 (1996)

    Article  CAS  ADS  Google Scholar 

  23. Greiner, M., Mandel, O., Hänsch, T. W. & Bloch, I. Collapse and revival of the matter wave field of a Bose-Einstein condensate. Nature 419, 51–54 (2002)

    Article  CAS  ADS  Google Scholar 

  24. Johnson, B. R. et al. Quantum non-demolition detection of single microwave photons in a circuit. Nature Phys. 6, 663–667 (2010)

    Article  CAS  ADS  Google Scholar 

  25. Solano, E. Selective interactions in trapped ions: state reconstruction and quantum logic. Phys. Rev. A 71, 013813 (2005)

    Article  ADS  Google Scholar 

  26. Milburn, G. Quantum and classical Liouville dynamics of the anharmonic-oscillator. Phys. Rev. A 33, 674–685 (1986)

    Article  CAS  ADS  MathSciNet  Google Scholar 

  27. Deléglise, S. et al. Reconstruction of non-classical cavity field states with snapshots of their decoherence. Nature 455, 510–514 (2008)

    Article  ADS  Google Scholar 

  28. Eichler, C., Bozyigit, D. & Wallraff, A. Characterizing quantum microwave radiation and its entanglement with superconducting qubits using linear detectors. Phys. Rev. A 86, 032106 (2012)

    Article  ADS  Google Scholar 

  29. Leibfried, D. et al. Experimental determination of the motional quantum state of a trapped atom. Phys. Rev. Lett. 77, 4281–4285 (1996)

    Article  CAS  ADS  Google Scholar 

  30. Leghtas, Z. et al. Hardware-efficient autonomous quantum error correction. Preprint at http://arXiv.org/abs/1207.0679 (2012)

Download references

Acknowledgements

We thank M. H. Devoret, M. D. Reed, M. Hatridge and A. Sears for discussions. This research was supported by the National Science Foundation (NSF) (PHY-0969725), the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Projects Activity (IARPA) through the Army Research Office (W911NF-09-1-0369), and the US Army Research Office (W911NF-09-1-0514). Use of facilities was supported by the Yale Institute for Nanoscience and Quantum Engineering (YINQE) and the NSF (MRSECDMR 1119826). S.M.G. acknowledges support from the NSF (DMR-1004406). M.M. and Z.L. acknowledge support from French Agence Nationale de la Recherche under the project EPOQ2 (ANR-09-JCJC-0070). S.E.N. acknowledges support from the Swiss NSF. E.G. acknowledges support from EPSRC (EP/I026231/1).

Author information

Authors and Affiliations

  1. Departments of Physics and Applied Physics, Yale University, New Haven, 06511, Connecticut, USA

    Gerhard Kirchmair, Brian Vlastakis, Simon E. Nigg, Hanhee Paik, Mazyar Mirrahimi, Luigi Frunzio, S. M. Girvin & R. J. Schoelkopf

  2. INRIA Paris-Rocquencourt, Domaine de Voluceau, BP 105, 78153 Le Chesnay Cedex, France,

    Zaki Leghtas & Mazyar Mirrahimi

  3. Department of Physics and Advanced Technology Institute, University of Surrey, Guildford, Surrey GU2 7XH, UK,

    Eran Ginossar

Authors
  1. Gerhard Kirchmair
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Brian Vlastakis
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zaki Leghtas
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Simon E. Nigg
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Hanhee Paik
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Eran Ginossar
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Mazyar Mirrahimi
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Luigi Frunzio
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. S. M. Girvin
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. R. J. Schoelkopf
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

G.K. and B.V. performed the experiments. G.K., B.V., Z.L. and M.M. analysed the data. G.K., B.V. and L.F. fabricated the qubits. G.K., B.V., H.P. and S.E.N. designed the device and calculated the device parameters. G.K., E.G., S.M.G. and R.J.S. conceived the experiment and all authors co-wrote the paper.

Corresponding author

Correspondence to R. J. Schoelkopf.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

This file contains Supplementary Text and Data, Supplementary Figures 1-5 and Supplementary References. (PDF 1186 kb)

Evolution of the Q function of a coherent state in a Kerr medium

This video shows the evolution of the Q function of a coherent state in a Kerr medium. The left frame shows the measured data while the right frame shows a simulation, which was obtained by numerically solving a master equation for the same interaction times. The total evolution was measured over 6.05µs, showing two coherent state revivals. (MOV 17414 kb)

PowerPoint slides

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kirchmair, G., Vlastakis, B., Leghtas, Z. et al. Observation of quantum state collapse and revival due to the single-photon Kerr effect. Nature 495, 205–209 (2013). https://doi.org/10.1038/nature11902

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nature11902

This article is cited by

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing