Abstract
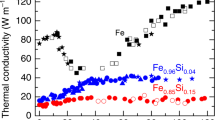
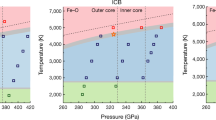
The Earth acts as a gigantic heat engine driven by the decay of radiogenic isotopes and slow cooling, which gives rise to plate tectonics, volcanoes and mountain building. Another key product is the geomagnetic field, generated in the liquid iron core by a dynamo running on heat released by cooling and freezing (as the solid inner core grows), and on chemical convection (due to light elements expelled from the liquid on freezing). The power supplied to the geodynamo, measured by the heat flux across the core–mantle boundary (CMB), places constraints on Earth’s evolution1. Estimates of CMB heat flux2,3,4,5 depend on properties of iron mixtures under the extreme pressure and temperature conditions in the core, most critically on the thermal and electrical conductivities. These quantities remain poorly known because of inherent experimental and theoretical difficulties. Here we use density functional theory to compute these conductivities in liquid iron mixtures at core conditions from first principles—unlike previous estimates, which relied on extrapolations. The mixtures of iron, oxygen, sulphur and silicon are taken from earlier work6 and fit the seismologically determined core density and inner-core boundary density jump7,8. We find both conductivities to be two to three times higher than estimates in current use. The changes are so large that core thermal histories and power requirements need to be reassessed. New estimates indicate that the adiabatic heat flux is 15 to 16 terawatts at the CMB, higher than present estimates of CMB heat flux based on mantle convection1; the top of the core must be thermally stratified and any convection in the upper core must be driven by chemical convection against the adverse thermal buoyancy or lateral variations in CMB heat flow. Power for the geodynamo is greatly restricted, and future models of mantle evolution will need to incorporate a high CMB heat flux and explain the recent formation of the inner core.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout


Similar content being viewed by others
References
Lay, T., Hernlund, J. & Buffett, B. Core-mantle boundary heat flow. Nature Geosci. 1, 25–32 (2008)
Labrosse, S., Poirier, J.-P. & Le Mouël, J.-L. On cooling of the Earth’s core. Phys. Earth Planet. Inter. 99, 1–17 (1997)
Buffett, B., Garnero, E. & Jeanloz, R. Sediments at the top of Earth’s core. Science 290, 1338–1342 (2000)
Lister, J. R. & Buffett, B. A. The strength and efficiency of thermal and compositional convection in the geodynamo. Phys. Earth Planet. Inter. 91, 17–30 (1995)
Gubbins, D., Alfè, D., Masters, T. G. & Price, D. Gross thermodynamics of 2-component core convection. Geophys. J. Int. 157, 1407–1414 (2004)
Alfè, D., Gillan, M. J. & Price, G. D. Temperature and composition of the Earth’s core. Contemp. Phys. 48, 63–80 (2007)
Masters, T. G. & Gubbins, D. On the resolution of density within the Earth. Phys. Earth Planet. Inter. 140, 159–167 (2003)
Dziewonski, A. M. & Anderson, D. L. Preliminary Reference Earth Model. Phys. Earth Planet. Inter. 25, 297–356 (1981)
Silvestrelli, P. L., Alavi, A. & Parrinello, M. Electrical conductivity calculation in ab initio simulations of metals: application to liquid sodium. Phys. Rev. B 55, 15515–15522 (1997)
Mattsson, T. R. & Desjarlais, M. P. Phase diagram and electrical conductivity of high energy density water from density functional theory. Phys. Rev. Lett. 97, 017801 (2007)
Pozzo, M., Desjarlais, M. P. & Alfè, D. Electrical and thermal conductivity of liquid sodium from first principles calculations. Phys. Rev. B 84, 054203 (2011)
Alfè, D., Gillan, M. J. & Price, G. D. The melting curve of iron at the pressures of the Earth’s core conditions. Nature 401, 462–464 (1999)
Alfè, D. Temperature of the inner-core boundary of the Earth: melting of iron at high pressure from first-principles coexistence simulations. Phys. Rev. B 79, 060101(R) (2009)
Alfè, D., Pozzo, M. & Desjarlais, M. P. Lattice electrical resistivity of magnetic body-centred cubic iron from first principles calculations. Phys. Rev. B 85, 024102 (2012)
Bi, Y., Tan, H. & Jing, F. Electrical conductivity of iron under shock compression up to 200 GPa. J. Phys. Condens. Matter 14, 10849–10854 (2002)
Keeler, R. N. & Royce, E. B. in Physics of High Energy Density (eds Caldirola, P. & Knoepfel, H. ) 106–125 (Proc. Int. Sch. Phys. Enrico Fermi Vol. 48, 1971)
Stacey, F. D. & Anderson, O. L. Electrical and thermal conductivities of Fe–Ni–Si alloy under core conditions. Phys. Earth Planet. Inter. 124, 153–162 (2001)
Hirose, K. Gomi, H. Ohta, K. Labrosse, S. & Hernlund, J. The high conductivity of iron and thermal evolution of the Earth’s core. Mineral. Mag. 75, 1027 (2011)
de Koker, N., Steinle-Neumann, G. & Vlcek, V. Electrical resistivity and thermal conductivity of liquid Fe alloys at high P and T, and heat flux in Earth's core. Proc. Natl Acad. Sci. 109, 4070–4073 (2012)
Davies, C. J. & Gubbins, D. A buoyancy profile for the Earth’s core. Geophys. J. Int. 187, 549–563 (2011)
Olson, P. in Earth’s Core and Lower Mantle (eds Jones, C., Soward, A. & Zhang, K. ) 1–49 (Taylor and Francis, London, 2000)
Nakagawa, T. &. Tackley, P. J. Lateral variations in CMB heat flux and deep mantle seismic velocity caused by a thermal-chemical-phase boundary layer in 3D spherical convection. Earth Planet. Sci. Lett. 271, 348–358 (2008)
Jackson, A., Jonkers, A. R. T. & Walker, M. R. Four centuries of geomagnetic secular variation from historical records. Phil. Trans. R. Soc. Lond. B 358, 957–990 (2000)
Gubbins, D. in Encyclopedia of Geomagnetism and Paleomagnetism (eds Gubbins, D. & Herrero-Bervera, E. ) 287–300 (Springer, 2007)
Davies, G. Topography: a robust constraint on mantle fluxes. Chem. Geol. 145, 479–489 (1998)
Davies, G. Mantle regulation of core cooling: a geodynamo without core radioactivity? Phys. Earth Planet. Inter. 160, 215–229 (2007)
McDonough, W. in Treatise on Geochemistry Vol. 2 (ed. Carlson, R. W. ) 547–568 (Elsevier, 2003)
Kresse, G. & Furthmuller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996)
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994)
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999)
Wang, Y. & Perdew, J. P. Correlation hole of the spin-polarized electron gas, with exact small-wave-vector and high-density scaling. Phys. Rev. B 44, 13298–13307 (1991)
Desjarlais, M. P., Kress, J. D. & Collins, L. A. Electrical conductivity for warm, dense aluminum plasmas and liquids. Phys. Rev. E 66, 025401(R) (2002)
Alfè, D. Ab initio molecular dynamics, a simple algorithm for charge extrapolation. Comput. Phys. Commun. 118, 31–33 (1999)
Buffett, B. A. Estimates of heat flow in the deep mantle based on the power requirements for the geodynamo. Geophys. Res. Lett. 29, 1566–1569 (2002)
Kuang, W. & Bloxham, J. An Earth-like numerical dynamo model. Nature 389, 371–374 (1997)
Gubbins, D., Alfè, D., Masters, T. G., Price, D. & Gillan, M. J. Can the Earth’s dynamo run on heat alone? Geophys. J. Int. 155, 609–622 (2003)
Anufriev, A. P., Jones, C. A. & Soward, A. M. The Boussinesq and anelastic liquid approximations for convection in the Earth’s core. Phys. Earth Planet. Inter. 152, 163–190 (2005)
Gubbins, D. & Roberts, P. H. in Geomagnetism (ed. Jacobs, J. A. ) 30–32 (Academic, 1987)
Acknowledgements
D.G. is supported by CSEDI grant EAR1065597 from the National Science Foundation. C.D. is supported by a Natural Environment Research Council personal fellowship, NE/H01571X/1. M.P. is supported by NERC grant NE/H02462X/1 to D.A. Calculations were performed on the UK national facility HECToR.
Author information
Authors and Affiliations
Contributions
D.A. and D.G. designed the project. M.P. and D.A. performed the first principles calculations. C.D. and D.G. performed the thermal history and core stratification calculations. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Tables
This file contains Supplementary Tables 1-3. (PDF 203 kb)
PowerPoint slides
Rights and permissions
About this article
Cite this article
Pozzo, M., Davies, C., Gubbins, D. et al. Thermal and electrical conductivity of iron at Earth’s core conditions. Nature 485, 355–358 (2012). https://doi.org/10.1038/nature11031
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature11031
This article is cited by
-
Regionally-triggered geomagnetic reversals
Scientific Reports (2024)
-
Mesoproterozoic geomagnetic field strength from Nova Guarita mafic dykes (Amazon Craton)
Studia Geophysica et Geodaetica (2023)
-
Sustaining Earth’s magnetic dynamo
Nature Reviews Earth & Environment (2022)
-
Anomalous thermal transport under high pressure in boron arsenide
Nature (2022)
-
Superionic iron alloys and their seismic velocities in Earth’s inner core
Nature (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.