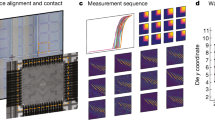
Abstract
The presence of long-range quantum spin correlations underlies a variety of physical phenomena in condensed-matter systems, potentially including high-temperature superconductivity1,2. However, many properties of exotic, strongly correlated spin systems, such as spin liquids, have proved difficult to study, in part because calculations involving N-body entanglement become intractable for as few as N ≈ 30 particles3. Feynman predicted that a quantum simulator—a special-purpose ‘analogue’ processor built using quantum bits (qubits)—would be inherently suited to solving such problems4,5. In the context of quantum magnetism, a number of experiments have demonstrated the feasibility of this approach6,7,8,9,10,11,12,13,14, but simulations allowing controlled, tunable interactions between spins localized on two- or three-dimensional lattices of more than a few tens of qubits have yet to be demonstrated, in part because of the technical challenge of realizing large-scale qubit arrays. Here we demonstrate a variable-range Ising-type spin–spin interaction, Ji,j , on a naturally occurring, two-dimensional triangular crystal lattice of hundreds of spin-half particles (beryllium ions stored in a Penning trap). This is a computationally relevant scale more than an order of magnitude larger than previous experiments. We show that a spin-dependent optical dipole force can produce an antiferromagnetic interaction  , where 0 ≤ a ≤ 3 and di,j is the distance between spin pairs. These power laws correspond physically to infinite-range (a = 0), Coulomb–like (a = 1), monopole–dipole (a = 2) and dipole–dipole (a = 3) couplings. Experimentally, we demonstrate excellent agreement with a theory for 0.05 ≲ a ≲ 1.4. This demonstration, coupled with the high spin count, excellent quantum control and low technical complexity of the Penning trap, brings within reach the simulation of otherwise computationally intractable problems in quantum magnetism.
, where 0 ≤ a ≤ 3 and di,j is the distance between spin pairs. These power laws correspond physically to infinite-range (a = 0), Coulomb–like (a = 1), monopole–dipole (a = 2) and dipole–dipole (a = 3) couplings. Experimentally, we demonstrate excellent agreement with a theory for 0.05 ≲ a ≲ 1.4. This demonstration, coupled with the high spin count, excellent quantum control and low technical complexity of the Penning trap, brings within reach the simulation of otherwise computationally intractable problems in quantum magnetism.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Anderson, P. W. The resonating valence bond state in La2CuO4 and superconductivity. Science 235, 1196–1198 (1987)
Moessner, R., Sondhi, S. L. & Chandra, P. Two-dimensional periodic frustrated Ising models in a transverse field. Phys. Rev. Lett. 84, 4457–4460 (2000)
Sandvik, A. W. Ground states of a frustrated quantum spin chain with long-range interactions. Phys. Rev. Lett. 104, 137204 (2010)
Feynman, R. Simulating physics with computers. Int. J. Theor. Phys. 21, 467–488 (1982)
Buluta, I. & Nori, F. Quantum simulators. Science 326, 108–111 (2009)
Trotzky, S. et al. Time-resolved observation and control of superexchange interactions with ultracold atoms in optical lattices. Science 319, 295–299 (2008)
Lin, Y.-J., Compton, R. L., Jiménez-García, K., Porto, J. V. & Spielman, I. B. Synthetic magnetic fields for ultracold neutral atoms. Nature 462, 628–632 (2009)
Jo, G.-B. et al. Itinerant ferromagnetism in a Fermi gas of ultracold atoms. Science 325, 1521–1524 (2009)
Friedenauer, A., Schmitz, H., Glueckert, J. T., Porras, D. & Schaetz, T. Simulating a quantum magnet with trapped ions. Nature Phys. 4, 757–761 (2008)
Kim, K. et al. Quantum simulation of frustrated Ising spins with trapped ions. Nature 465, 590–593 (2010)
Simon, J. et al. Quantum simulation of antiferromagnetic spin chains in an optical lattice. Nature 472, 307–312 (2011)
Ma, X.-s., Dakic, B., Naylor, W., Zeilinger, A. & Walther, P. Quantum simulation of the wavefunction to probe frustrated Heisenberg spin systems. Nature Phys. 7, 399–405 (2011)
Islam, R. et al. Onset of a quantum phase transition with a trapped ion quantum simulator. Nature Commun. 2, 377 (2011)
Lanyon, B. P. et al. Universal digital quantum simulation with trapped ions. Science 334, 57–61 (2011)
Sachdev, S. Quantum Phase Transitions (Cambridge Univ. Press, 2001)
Kohno, M., Starykh, O., a & Balents, L. Spinons and triplons in spatially anisotropic frustrated antiferromagnets. Nature Phys. 3, 790–795 (2007)
Varney, C., Sun, K., Galitski, V. & Rigol, M. Kaleidoscope of exotic quantum phases in a frustrated XY model. Phys. Rev. Lett. 107, 077201 (2011)
Levi, B. G. New candidate emerges for a quantum spin liquid. Phys. Today 60, 16–19 (2007)
Helton, J. S. et al. Spin dynamics of the spin-1/2 Kagome lattice antiferromagnet ZnCu3(OH)6Cl2 . Phys. Rev. Lett. 98, 107204 (2007)
Balents, L. Spin liquids in frustrated magnets. Nature 464, 199–208 (2010)
Lewenstein, M. et al. Ultracold atomic gases in optical lattices: mimicking condensed matter physics and beyond. Adv. Phys. 56, 243–379 (2007)
Bloch, I. & Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 80, 885–964 (2008)
Rosenband, T. et al. Frequency ratio of Al+ and Hg+ single-ion optical clocks; metrology at the 17th decimal place. Science 319, 1808–1812 (2008)
Schmied, R., Wesenberg, J. H. & Leibfried, D. Optimal surface-electrode trap lattices for quantum simulation with trapped ions. Phys. Rev. Lett. 102, 233002 (2009)
Biercuk, M. J. et al. High-fidelity quantum control using ion crystals in a Penning trap. Quantum Inf. Comput. 9, 920–949 (2009)
Mitchell, T. et al. Direct observations of structural phase transitions in planar crystallized ion plasmas. Science 282, 1290–1293 (1998)
Leibfried, D. et al. Experimental demonstration of a robust, high-fidelity geometric two ion-qubit phase gate. Nature 422, 412–415 (2003)
Porras, D. & Cirac, J. Quantum manipulation of trapped ions in two dimensional coulomb crystals. Phys. Rev. Lett. 96, 250501 (2006)
Kim, K. et al. Entanglement and tunable spin-spin couplings between trapped ions using multiple transverse modes. Phys. Rev. Lett. 103, 120502 (2009)
Sawyer, B. C. et al. Spectroscopy and thermometry of drumhead modes in a mesoscopic trapped-ion crystal using entanglement. Phys. Rev. Lett. (in the press); preprint at 〈http://arxiv.org/abs/1201.4415〉 (2012)
Acknowledgements
This work was supported by the DARPA OLE programme and NIST. A.C.K. was supported by the NSF under grant number DMR-1004268. B.C.S. is supported by an NRC fellowship funded by NIST. J.K.F. was supported by the McDevitt endowment bequest at Georgetown University. M.J.B. and J.J.B. acknowledge partial support from the Australian Research Council Center of Excellence for Engineered Quantum Systems CE110001013. We thank F. Da Silva, R. Jordens, D. Leibfried, A. O’Brien, R. Scalettar and A. M. Rey for discussions.
Author information
Authors and Affiliations
Contributions
J.W.B., B.C.S., H.U., M.J.B. and J.J.B designed the experiment. J.W.B. and B.C.S. obtained the data and analysed it with advice from J.J.B. A.C.K., C.-C.J.W. and J.K.F. developed the formalism and numerics to calculate the spin–spin coupling. J.W.B. wrote the manuscript with assistance from B.C.S., M.J.B. and J.J.B. All authors participated in discussions, contributed ideas throughout the project and edited the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
This manuscript is a contribution of the US National Institute of Standards and Technology and is not subject to US copyright.
Supplementary information
Supplementary Information
This file contains Supplementary Text and Data, Supplementary Figures 1-7 and Supplementary References. (PDF 1069 kb)
Rights and permissions
About this article
Cite this article
Britton, J., Sawyer, B., Keith, A. et al. Engineered two-dimensional Ising interactions in a trapped-ion quantum simulator with hundreds of spins. Nature 484, 489–492 (2012). https://doi.org/10.1038/nature10981
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature10981
This article is cited by
-
Tunable quantum simulation of spin models with a two-dimensional ion crystal
Nature Physics (2024)
-
Quantum entanglement of ions for light dark matter detection
Journal of High Energy Physics (2024)
-
Mixed state behavior of Hermitian and non-Hermitian topological models with extended couplings
Scientific Reports (2023)
-
Quantum-enhanced sensing on optical transitions through finite-range interactions
Nature (2023)
-
Entanglement propagation and dynamics in non-additive quantum systems
Scientific Reports (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.