Abstract
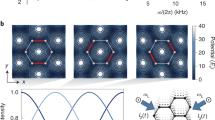
Dirac points are central to many phenomena in condensed-matter physics, from massless electrons in graphene to the emergence of conducting edge states in topological insulators1,2. At a Dirac point, two energy bands intersect linearly and the electrons behave as relativistic Dirac fermions. In solids, the rigid structure of the material determines the mass and velocity of the electrons, as well as their interactions. A different, highly flexible means of studying condensed-matter phenomena is to create model systems using ultracold atoms trapped in the periodic potential of interfering laser beams3,4. Here we report the creation of Dirac points with adjustable properties in a tunable honeycomb optical lattice. Using momentum-resolved interband transitions, we observe a minimum bandgap inside the Brillouin zone at the positions of the two Dirac points. We exploit the unique tunability of our lattice potential to adjust the effective mass of the Dirac fermions by breaking inversion symmetry. Moreover, changing the lattice anisotropy allows us to change the positions of the Dirac points inside the Brillouin zone. When the anisotropy exceeds a critical limit, the two Dirac points merge and annihilate each other—a situation that has recently attracted considerable theoretical interest5,6,7,8,9 but that is extremely challenging to observe in solids10. We map out this topological transition in lattice parameter space and find excellent agreement with ab initio calculations. Our results not only pave the way to model materials in which the topology of the band structure is crucial, but also provide an avenue to exploring many-body phases resulting from the interplay of complex lattice geometries with interactions11,12,13.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Castro Neto, A. H., Guinea, F., Peres, N. M. R., Novoselov, K. S. & Geim, A. K. The electronic properties of graphene. Rev. Mod. Phys. 81, 109–162 (2009)
Hasan, M. Z. & Kane, C. L. Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010)
Lewenstein, M. et al. Ultracold atomic gases in optical lattices: mimicking condensed matter physics and beyond. Adv. Phys. 56, 243–379 (2007)
Bloch, I., Dalibard, J. & Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 80, 885–964 (2008)
Hasegawa, Y., Konno, R., Nakano, H. & Kohmoto, M. Zero modes of tight-binding electrons on the honeycomb lattice. Phys. Rev. B 74, 033413 (2006)
Zhu, S.-L., Wang, B. & Duan, L.-M. Simulation and detection of Dirac fermions with cold atoms in an optical lattice. Phys. Rev. Lett. 98, 260402 (2007)
Wunsch, B. Guinea, F. & Sols, F. Dirac-point engineering and topological phase transitions in honeycomb optical lattices. N. J. Phys. 10, 103027 (2008)
Montambaux, G., Piéchon, F., Fuchs, J.-N. & Goerbig, M. O. Merging of Dirac points in a two-dimensional crystal. Phys. Rev. B 80, 153412 (2009)
Lee, K. L., Grémaud, B., Han, R., Englert, B.-G. & Miniatura, C. Ultracold fermions in a graphene-type optical lattice. Phys. Rev. A 80, 043411 (2009)
Pereira, V. M., Castro Neto, A. H. & Peres, N. M. R. Tight-binding approach to uniaxial strain in graphene. Phys. Rev. B 80, 045401 (2009)
Zhao, E. & Paramekanti, A. BCS-BEC crossover on the two-dimensional honeycomb lattice. Phys. Rev. Lett. 97, 230404 (2006)
Balents, L. Spin liquids in frustrated magnets. Nature 464, 199–208 (2010)
Meng, Z. Y., Lang, T. C., Wessel, S., Assaad, F. F. & Muramatsu, A. Quantum spin liquid emerging in two-dimensional correlated Dirac fermions. Nature 464, 847–851 (2010)
Greiner, M., Mandel, O., Esslinger, T., Hänsch, T. W. & Bloch, I. Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature 415, 39–44 (2002)
Jördens, R., Strohmaier, N., Günter, K., Moritz, H. & Esslinger, T. A Mott insulator of fermionic atoms in an optical lattice. Nature 455, 204–207 (2008)
Schneider, U. et al. Metallic and insulating phases of repulsively interacting fermions in a 3D optical lattice. Science 322, 1520–1525 (2008)
Soltan-Panahi, P. et al. Multi-component quantum gases in spin-dependent hexagonal lattices. Nature Phys. 7, 434–440 (2011)
Soltan-Panahi, P., Lühmann, D.-S., Struck, J., Windpassinger, P. & Sengstock, K. Quantum phase transition to unconventional multi-orbital superfluidity in optical lattices. Nature Phys. 8, 71–75 (2012)
Salger, T., Geckeler, C., Kling, S. & Weitz, M. Atomic Landau-Zener tunneling in Fourier-synthesized optical lattices. Phys. Rev. Lett. 99, 190405 (2007)
Asano, K. & Hotta, C. Designing Dirac points in two-dimensional lattices. Phys. Rev. B 83, 245125 (2011)
Ben Dahan, M., Peik, E., Reichel, J., Castin, Y. & Salomon, C. Bloch oscillations of atoms in an optical potential. Phys. Rev. Lett. 76, 4508–4511 (1996)
Köhl, M., Moritz, H., Stöferle, T., Günter, K. & Esslinger, T. Fermionic atoms in a three dimensional optical lattice: observing Fermi surfaces, dynamics, and interactions. Phys. Rev. Lett. 94, 080403 (2005)
Kling, S., Salger, T., Grossert, C. & Weitz, M. Atomic Bloch-Zener oscillations and Stückelberg interferometry in optical lattices. Phys. Rev. Lett. 105, 215301 (2010)
Zenesini, A., Ciampini, D., Morsch, O. & Arimondo, E. Observation of Stückelberg oscillations in accelerated optical lattices. Phys. Rev. A 82, 065601 (2010)
Lin, Y.-J., Compton, R. L., Jiménez-García, K., Porto, J. V. & Spielman, I. B. Synthetic magnetic fields for ultracold neutral atoms. Nature 462, 628–632 (2009)
Kitagawa, T., Berg, E., Rudner, M. & Demler, E. Topological characterization of periodically driven quantum systems. Phys. Rev. B 82, 235114 (2010)
Lubasch, M., Murg, V., Schneider, U., Cirac, J. I. & Bañuls, M.-C. Adiabatic preparation of a Heisenberg antiferromagnet using an optical superlattice. Phys. Rev. Lett. 107, 165301 (2011)
Sachdev, S. Quantum magnetism and criticality. Nature Phys. 4, 173–185 (2008)
Hemmerich, A., Schropp, D., Esslinger, T. & Hänsch, T. W. Elastic scattering of rubidium atoms by two crossed standing waves. Europhys. Lett. 18, 391–395 (1992)
Ma, L.-S., Jungner, P., Ye, J. & Hall, J. L. Delivering the same optical frequency at two places: accurate cancellation of phase noise introduced by an optical fiber or other time-varying path. Opt. Lett. 19, 1777–1779 (1994)
Acknowledgements
We would like to thank D. Poletti for bringing our attention to honeycomb lattices without six-fold symmetry, and N. Cooper and F. Hassler for discussions. We acknowledge SNF, NCCR-MaNEP, NCCR-QSIT, NAME-QUAM (EU, FET open), SQMS (ERC advanced grant) and ESF (POLATOM) for funding.
Author information
Authors and Affiliations
Contributions
The data were measured and analysed by L.T., D.G., T.U. and G.J. The tunable optical lattice was built by D.G. The experimental concept was developed by T.E. All authors contributed extensively to the discussion of the results, as well as to the preparation of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Tarruell, L., Greif, D., Uehlinger, T. et al. Creating, moving and merging Dirac points with a Fermi gas in a tunable honeycomb lattice. Nature 483, 302–305 (2012). https://doi.org/10.1038/nature10871
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature10871
This article is cited by
-
Quantization and its breakdown in a Hubbard–Thouless pump
Nature Physics (2023)
-
Frustration- and doping-induced magnetism in a Fermi–Hubbard simulator
Nature (2023)
-
Many-body quantum chaos in stroboscopically-driven cold atoms
Communications Physics (2023)
-
Revealing inherent quantum interference and entanglement of a Dirac particle
npj Quantum Information (2023)
-
Tunable Dirac points in a two-dimensional non-symmorphic wallpaper group lattice
Communications Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.