Abstract
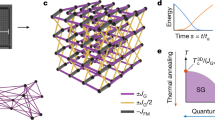
Many interesting but practically intractable problems can be reduced to that of finding the ground state of a system of interacting spins; however, finding such a ground state remains computationally difficult1. It is believed that the ground state of some naturally occurring spin systems can be effectively attained through a process called quantum annealing2,3. If it could be harnessed, quantum annealing might improve on known methods for solving certain types of problem4,5. However, physical investigation of quantum annealing has been largely confined to microscopic spins in condensed-matter systems6,7,8,9,10,11,12. Here we use quantum annealing to find the ground state of an artificial Ising spin system comprising an array of eight superconducting flux quantum bits with programmable spin–spin couplings. We observe a clear signature of quantum annealing, distinguishable from classical thermal annealing through the temperature dependence of the time at which the system dynamics freezes. Our implementation can be configured in situ to realize a wide variety of different spin networks, each of which can be monitored as it moves towards a low-energy configuration13,14. This programmable artificial spin network bridges the gap between the theoretical study of ideal isolated spin networks and the experimental investigation of bulk magnetic samples. Moreover, with an increased number of spins, such a system may provide a practical physical means to implement a quantum algorithm, possibly allowing more-effective approaches to solving certain classes of hard combinatorial optimization problems.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Barahona, F. On the computational complexity of Ising spin glass models. J. Phys. Math. Gen. 15, 3241–3253 (1982)
Kadowaki, T. & Nishimori, H. Quantum annealing in the transverse Ising model. Phys. Rev. E 58, 5355–5363 (1998)
Finnila, A. B., Gomez, M. A., Sebenik, C., Stenson, C. & Doll, J. D. Quantum annealing: a new method for minimizing multidimensional functions. Chem. Phys. Lett. 219, 343–348 (1994)
Farhi, E. et al. A quantum adiabatic evolution algorithm applied to random instances of an NP-complete problem. Science 292, 472–475 (2001)
Hogg, T. Quantum search heuristics. Phys. Rev. A 61, 052311 (2000)
Wernsdorfer, W. Molecular nanomagnets: towards molecular spintronics. Int. J. Nanotechnol. 7, 497–522 (2010)
Carretta, S., Liviotti, E., Magnani, N., Santini, P. & Amoretti, G. S mixing and quantum tunneling of the magnetization in molecular nanomagnets. Phys. Rev. Lett. 92, 207205 (2004)
Caciuffo, R. et al. Spin dynamics of heterometallic Cr7M wheels (M = Mn, Zn, Ni) probed by inelastic neutron scattering. Phys. Rev. B 71, 174407 (2005)
Guidi, T. et al. Inelastic neutron scattering study of the molecular grid nanomagnet Mn-[3 × 3]. Phys. Rev. B 69, 104432 (2004)
Waldmann, O., Guidi, T., Carretta, S., Mondelli, C. & Dearden, A. L. Elementary excitations in the cyclic molecular nanomagnet Cr8 . Phys. Rev. Lett. 91, 237202 (2003)
Brooke, J., Bitko, D., Rosenbaum, T. F. & Aeppli, G. Quantum annealing of a disordered magnet. Science 284, 779–781 (1999)
Ghosh, S. & Rosenbaum, T. F. Aeppli, G. & Coppersmith, S. N. Entangled quantum state of magnetic dipoles. Nature 425, 48–51 (2003)
Harris, R. et al. Experimental demonstration of a robust and scalable flux qubit. Phys. Rev. B 81, 134510 (2010)
Harris, R. et al. Experimental investigation of an eight-qubit unit cell in a superconducting optimization processor. Phys. Rev. B 82, 024511 (2010)
Aharonov, D. et al. Adiabatic quantum computation is equivalent to standard quantum computation. SIAM J. Comput. 37, 166–194 (2007)
Hinton, G. E. & Salakhutdinov, R. R. Reducing the dimensionality of data with neural networks. Science 313, 504–507 (2006)
Chen, X. & Tompa, M. Comparative assessment of methods for aligning multiple genome sequences. Nature Biotechnol. 28, 567–572 (2010)
Steffen, M., van Dam, W., Hogg, T., Breyta, G. & Chuang, I. Experimental implementation of an adiabatic quantum optimization algorithm. Phys. Rev. Lett. 90, 067903 (2003)
Kim, K. et al. Quantum simulation of frustrated Ising spins with trapped ions. Nature 465, 590–593 (2010)
Lupas¸cu, A. et al. Quantum non-demolition measurement of a superconducting two-level system. Nature Phys. 3, 119–125 (2007)
Berns, D. M. et al. Amplitude spectroscopy of a solid-state artificial atom. Nature 455, 51–58 (2008)
Poletto, S. et al. Coherent oscillations in a superconducting tunable flux qubit manipulated without microwaves. N. J. Phys. 11, 013009 (2009)
DiCarlo, L. et al. Demonstration of two-qubit algorithms with a superconducting quantum processor. Nature 460, 240–244 (2009)
Bennett, D. A. et al. Decoherence in rf SQUID qubits. Quantum Inf. Process. 8, 217–243 (2009)
Yoshihara, F., Nakamura, Y. & Tsai, J. S. Correlated flux noise and decoherence in two inductively coupled flux qubits. Phys. Rev. B 81, 132502 (2010)
Il’ichev, E. et al. Multiphoton excitations and inverse population in a system of two flux qubits. Phys. Rev. B 81, 012506 (2010)
Vion, D. et al. Manipulating the quantum state of an electrical circuit. Science 296, 886–889 (2002)
Burkard, G., Koch, R. H. & DiVincenzo, D. P. Multilevel quantum description of decoherence in superconducting qubits. Phys. Rev. B 69, 064503 (2004)
Harris, R. et al. Compound Josephson-junction coupler for flux qubits with minimal crosstalk. Phys. Rev. B 80, 052506 (2009)
Voss, R. F. & Webb, R. A. Macroscopic quantum tunneling in 1-μm Nb Josephson junctions. Phys. Rev. Lett. 47, 265–268 (1981)
Devoret, M. H., Martinis, J. M. & Clarke, J. Measurements of macroscopic quantum tunneling out of the zero-voltage state of a current-biased josephson junction. Phys. Rev. Lett. 55, 1908–1911 (1985)
Biamonte, J. D. & Love, P. J. Realizable Hamiltonians for universal adiabatic quantum computers. Phys. Rev. A 78, 012352 (2008)
Harris, R. et al. Probing noise in flux qubits via macroscopic resonant tunneling. Phys. Rev. Lett. 101, 117003 (2008)
Acknowledgements
We would like to thank J. Preskill, A. Kitaev, D. A. Lidar, F. Wilhelm, A. Lupas¸cu, A. Blais, T. A. Brun, P. Smith, F. Altomare, E. Hoskinson, T. Przybysz, T. Mahon and R. Neufeld for discussions. We are grateful to the volunteers of the AQUA@home BOINC project for their help in running the classical simulations.
Author information
Authors and Affiliations
Contributions
M.H.S.A. and M.W.J. developed the idea for the experiment; M.W.J. conducted the experiment; T.L., R.H., M.W.J. and J.W. conducted supporting experiments; M.H.S.A. developed the theory; N.D., F.H. and M.H.S.A. developed simulation code; N.D., M.H.S.A., M.W.J., F.H. and C.J.S.T. performed simulations and analysed results; M.W.J., M.H.S.A., S.G. and R.H. wrote the article; M.W.J., S.G., M.H.S.A. and N.D. generated the figures; A.J.B., R.H., J.J., M.W.J., T.L., I.P., E.M.C. and B.W. developed measurement algorithms and testing software; C.R., S.U. and M.C.T. achieved the low-magnetic-field environment for the device; C.E. and C.R. mounted the sample, P.B., E.T., A.J.B., R.H., J.J., M.W.J. and T.L. designed the devices; E.L., N.L. and T.O. fabricated the devices; M.C.T. and S.U. developed the testing apparatus; K.K. allowed use of BOINC for classical simulations; J.P.H. and G.R. provided logistical support; and J.P.H. selected the chip.
Corresponding author
Ethics declarations
Competing interests
Some of the authors are employees of D-Wave Systems Inc., a company seeking to develop a processor that uses a computational model known as quantum annealing. This work describes progress in that effort.
Supplementary information
Supplementary Information
This file contains Supplementary Text and Data comprising I Overview; II Experiment and III Simulations (see contents list for full details), Supplementary Figures 1. (PDF 1421 kb)
Rights and permissions
About this article
Cite this article
Johnson, M., Amin, M., Gildert, S. et al. Quantum annealing with manufactured spins. Nature 473, 194–198 (2011). https://doi.org/10.1038/nature10012
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature10012
This article is cited by
-
Development of optimization method for truss structure by quantum annealing
Scientific Reports (2024)
-
Efficiency optimization in quantum computing: balancing thermodynamics and computational performance
Scientific Reports (2024)
-
Quantum annealing in Sherrington–Kirkpatrick spin glass in presence of time-dependent longitudinal field
Indian Journal of Physics (2024)
-
Convergence of the quantum dynamics framework for optimization algorithm
Quantum Information Processing (2024)
-
Scalable and robust quantum computing on qubit arrays with fixed coupling
npj Quantum Information (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.