Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Observation of scale invariance and universality in two-dimensional Bose gases

Nature volume 470, pages 236–239 (2011)Cite this article

Abstract

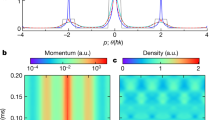
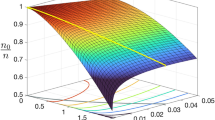
The collective behaviour of a many-body system near a continuous phase transition is insensitive to the details of its microscopic physics; for example, thermodynamic observables follow generalized scaling laws near the phase transition1. The Berezinskii–Kosterlitz–Thouless (BKT) phase transition2,3 in two-dimensional Bose gases presents a particularly interesting case because the marginal dimensionality and intrinsic scaling symmetry4 result in a broad fluctuation regime and an extended range of universal scaling behaviour. Studies of the BKT transition in cold atoms have stimulated great interest in recent years5,6,7,8,9,10, but a clear demonstration of critical behaviour near the phase transition has remained elusive. Here we report in situ density and density-fluctuation measurements of two-dimensional Bose gases of caesium at different temperatures and interaction strengths, observing scale-invariant, universal behaviours. The extracted thermodynamic functions confirm the existence of a wide universal region near the BKT phase transition, and provide a sensitive test of the universality predicted by classical-field theory11,12 and quantum Monte Carlo calculations13. Our experimental results provide evidence for growing density–density correlations in the fluctuation region, and call for further explorations of universal phenomena in classical and quantum critical physics.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Illustration of scale invariance and universality in 2D quantum gases.
Figure 2: Scale invariance of density and its fluctuation.
Figure 3: Universal behaviour near the BKT critical point.
Figure 4: Fluctuation versus compressibility.

References

  1. Stanley, H. E. Scaling, universality, and renormalization: three pillars of modern critical phenomena. Rev. Mod. Phys. 71, S358–S366 (1999)

    Article  CAS  Google Scholar 

  2. Berezinskii, V. L. Destruction of long-range order in one-dimensional and two-dimensional systems possessing a continuous symmetry group — II. Quantum systems. Sov. Phys. JETP 34, 610–616 (1972)

    ADS  Google Scholar 

  3. Kosterlitz, J. M. & Thouless, D. J. Ordering, metastability and phase-transitions in 2 dimensional systems. J. Phys. Chem. 6, 1181–1203 (1973)

    CAS  Google Scholar 

  4. Pitaevskii, L. P. & Rosch, A. Breathing modes and hidden symmetry of trapped atoms in two dimensions. Phys. Rev. A 55, R853–R856 (1997)

    Article  ADS  CAS  Google Scholar 

  5. Hadzibabic, Z., Krüger, P., Cheneau, M., Battelier, B. & Dalibard, J. Berezinskii-Kosterlitz-Thouless crossover in a trapped atomic gas. Nature 441, 1118–1121 (2006)

    Article  ADS  CAS  Google Scholar 

  6. Krüger, P., Hadzibabic, Z. & Dalibard, J. Critical point of an interacting two-dimensional atomic Bose gas. Phys. Rev. Lett. 99, 040402 (2007)

    Article  ADS  Google Scholar 

  7. Schweikhard, V., Tung, S. & Cornell, E. A. Vortex proliferation in the Berezinskii-Kosterlitz-Thouless regime on a two-dimensional lattice of Bose-Einstein condensates. Phys. Rev. Lett. 99, 030401 (2007)

    Article  ADS  CAS  Google Scholar 

  8. Cladé, P., Ryu, C., Ramanathan, A., Helmerson, K. & Phillips, W. D. Observation of a 2D Bose gas: from thermal to quasicondensate to superfluid. Phys. Rev. Lett. 102, 170401 (2009)

    Article  ADS  Google Scholar 

  9. Hadzibabic, Z., Krüger, P., Cheneau, M., Rath, S. P. & Dalibard, J. The trapped two-dimensional Bose gas: from Bose-Einstein condensation to Berezinskii-Kosterlitz-Thouless physics. N. J. Phys. 10, 045006 (2008)

    Article  Google Scholar 

  10. Tung, S., Lamporesi, G., Lobser, D., Xia, L. & Cornell, E. A. Observation of the pre-superfluid regime in a two-dimensional Bose gas. Phys. Rev. Lett. 105, 230408 (2010)

    Article  ADS  CAS  Google Scholar 

  11. Prokof'ev, N., Ruebenacker, O. & Svistunov, B. Critical point of a weakly interacting two-dimensional Bose gas. Phys. Rev. Lett. 87, 270402 (2001)

    Article  CAS  Google Scholar 

  12. Prokof'ev, N. & Svistunov, B. Two-dimensional weakly interacting Bose gas in the fluctuation region. Phys. Rev. A 66, 043608 (2002)

    Article  ADS  Google Scholar 

  13. Holzmann, M., Chevallier, M. & Krauth, W. Universal correlations and coherence in quasi-two-dimensional trapped Bose gases. Phys. Rev. A 81, 043622 (2010)

    Article  ADS  Google Scholar 

  14. Holzmann, M., Baym, G., Blaizot, J.-P. & Laloë, F. Superfluid transition of homogeneous and trapped two-dimensional Bose gases. Proc. Natl Acad. Sci. USA 104, 1476–1481 (2007)

    Article  ADS  MathSciNet  CAS  Google Scholar 

  15. Petrov, D. S., Holzmann, M. & Shlyapnikov, G. V. Bose-Einstein condensation in quasi-2D trapped gases. Phys. Rev. Lett. 84, 2551–2555 (2000)

    Article  ADS  CAS  Google Scholar 

  16. Chin, C., Grimm, R., Julienne, P. & Tiesinga, E. Feshbach resonances in ultracold gases. Rev. Mod. Phys. 82, 1225–1286 (2010)

    Article  ADS  CAS  Google Scholar 

  17. Gemelke, N., Zhang, X., Hung, C.-L. & Chin, C. In situ observation of incompressible Mott-insulating domains in ultracold atomic gases. Nature 460, 995–998 (2009)

    Article  ADS  CAS  Google Scholar 

  18. Hung, C.-L., Zhang, X., Gemelke, N. & Chin, C. Slow mass transport and statistical evolution of an atomic gas across the superfluid-Mott insulator transition. Phys. Rev. Lett. 104, 160403 (2010)

    Article  ADS  Google Scholar 

  19. Mora, C. & Castin, Y. Ground state energy of the two-dimensional weakly interacting Bose gas: first correction beyond Bogoliubov theory. Phys. Rev. Lett. 102, 180404 (2009)

    Article  ADS  Google Scholar 

  20. Simula, T. P., Davis, M. J. & Blakie, P. B. Superfluidity of an interacting trapped quasi-two-dimensional Bose gas. Phys. Rev. A 77, 023618 (2008)

    Article  ADS  Google Scholar 

  21. Rath, S. P. et al. Equilibrium state of a trapped two-dimensional Bose gas. Phys. Rev. A 82, 013609 (2010)

    Article  ADS  Google Scholar 

  22. Holzmann, M. & Krauth, W. Kosterlitz-Thouless transition of the quasi-two-dimensional trapped Bose gas. Phys. Rev. Lett. 100, 190402 (2008)

    Article  ADS  Google Scholar 

  23. Popov, V. N. Functional Integrals in Quantum Field Theory and Statistical Physics (Reidel, 1983)

    Book  Google Scholar 

  24. Bisset, R. N., Davis, M. J., Simula, T. P. & Blakie, P. B. Quasicondensation and coherence in the quasi-two-dimensional trapped Bose gas. Phys. Rev. A 79, 033626 (2009)

    Article  ADS  Google Scholar 

  25. Huang, K. Statistical Mechanics 152–154 (Wiley, 1963)

    Google Scholar 

  26. Kubo, R. The fluctuation-dissipation theorem. Rep. Prog. Phys. 29, 255–283 (1966)

    Article  ADS  CAS  Google Scholar 

  27. Toda, M., Kubo, R. & Saitô, N. Statistical Physics I: Equilibrium Statistical Mechanics (Springer, 1983)

    Book  Google Scholar 

  28. Zhou. Q. & Ho, T.-L. Universal thermometry for quantum simulation. Preprint at 〈http://arXiv.org/abs/0908.3015v2〉 (2009)

  29. Naraschewski, M. & Glauber, R. J. Spatial coherence and density correlations of trapped Bose gases. Phys. Rev. A 59, 4595–4607 (1999)

    Article  ADS  CAS  Google Scholar 

  30. Donner, T. et al. Critical behavior of a trapped interacting Bose gas. Science 315, 1556–1558 (2007)

    Article  ADS  CAS  Google Scholar 

  31. Reinaudi, G., Lahaye, T., Wang, Z. & Guéry-Odelin, D. Strong saturation absorption imaging of dense clouds of ultracold atoms. Opt. Lett. 32, 3143–3145 (2007)

    Article  ADS  CAS  Google Scholar 

Download references

Acknowledgements

We thank Q. Zhou, B. Svistunov, T.-L. Ho, Y. Castin, C.-C. Chien, S. Tung, N. Prokof'ev, J. Freerick and D.-W. Wang for discussions. This work was supported by the NSF (grant numbers PHY-0747907, NSF-MRSEC DMR-0213745), the Packard Foundation, and a grant from the Army Research Office with funding from the DARPA OLE program. N.G. acknowledges support from the Grainger Foundation.

Author information

Author notes

  1. Nathan Gemelke

    Present address: Present address: Department of Physics, The Pennsylvania State University, University Park, Pennsylvania 16802, USA.,

Authors and Affiliations

  1. The James Franck Institute and Department of Physics, University of Chicago, Chicago, 60637, Illinois, USA

    Chen-Lung Hung, Xibo Zhang, Nathan Gemelke & Cheng Chin

Authors
  1. Chen-Lung Hung
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xibo Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Nathan Gemelke
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Cheng Chin
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

The data were taken and analysed by C.-L.H. The experimental concept was developed by C.-L.H. and C.C. All authors contributed to discussion of the results and preparation of the manuscript.

Corresponding author

Correspondence to Chen-Lung Hung.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

PowerPoint slides

Rights and permissions

Reprints and Permissions

About this article

Cite this article

Hung, CL., Zhang, X., Gemelke, N. et al. Observation of scale invariance and universality in two-dimensional Bose gases. Nature 470, 236–239 (2011). https://doi.org/10.1038/nature09722

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nature09722

This article is cited by

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing