Abstract
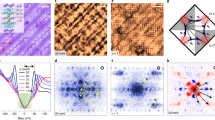
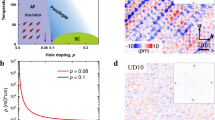
In the high-transition-temperature (high-Tc) superconductors the pseudogap phase becomes predominant when the density of doped holes is reduced1. Within this phase it has been unclear which electronic symmetries (if any) are broken, what the identity of any associated order parameter might be, and which microscopic electronic degrees of freedom are active. Here we report the determination of a quantitative order parameter representing intra-unit-cell nematicity: the breaking of rotational symmetry by the electronic structure within each CuO2 unit cell. We analyse spectroscopic-imaging scanning tunnelling microscope images of the intra-unit-cell states in underdoped Bi2Sr2CaCu2O8 + δ and, using two independent evaluation techniques, find evidence for electronic nematicity of the states close to the pseudogap energy. Moreover, we demonstrate directly that these phenomena arise from electronic differences at the two oxygen sites within each unit cell. If the characteristics of the pseudogap seen here and by other techniques all have the same microscopic origin, this phase involves weak magnetic states at the O sites that break 90°-rotational symmetry within every CuO2 unit cell.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Orenstein, J. & Millis, A. J. Advances in the physics of high-temperature superconductivity. Science 288, 468–474 (2000)
Zaanen, J., Sawatzky, G. A. & Allen, J. W. Band gaps and electronic structure of transition-metal compounds. Phys. Rev. Lett. 55, 418–421 (1985)
Hüfner, S., Hossain, M. A., Damascelli, A. & Sawatzky, G. A. Two gaps make a high-temperature superconductor? Rep. Prog. Phys. 71, 062501 (2008)
Alldredge, J. W. et al. Evolution of the electronic excitation spectrum with strongly diminishing hole density in superconducting Bi2Sr2CaCu2O8 + δ . Nature Phys. 4, 319–326 (2008)
Kohsaka, Y. et al. An intrinsic bond-centered electronic glass with unidirectional domains in underdoped cuprates. Science 315, 1380–1385 (2007)
Lee, J. et al. Spectroscopic fingerprint of phase-incoherent superconductivity in the cuprate pseudogap state. Science 325, 1099–1103 (2009)
McElroy, K. et al. Coincidence of checkerboard charge order and antinodal state decoherence in strongly underdoped superconducting Bi2Sr2CaCu2O8 + δ . Phys. Rev. Lett. 94, 197005 (2005)
Kohsaka, Y. et al. How Cooper pairs vanish approaching the Mott insulator in Bi2Sr2CaCu2O8 + δ . Nature 454, 1072–1078 (2008)
Maestro, A. D., Rosenow, B. & Sachdev, S. From stripe to checkerboard ordering of charge-density waves on the square lattice in the presence of quenched disorder. Phys. Rev. B 74, 024520 (2006)
Robertson, J. A., Kivelson, S. A., Fradkin, E., Fang, A. C. & Kapitulnik, A. Distinguishing patterns of charge order: stripes or checkerboards. Phys. Rev. B 74, 134507 (2006)
Kivelson, S. A., Fradkin, E. & Emery, V. J. Electronic liquid-crystal phases of a doped Mott insulator. Nature 393, 550–553 (1998)
Kivelson, S. A. et al. How to detect fluctuating stripes in the high-temperature superconductors. Rev. Mod. Phys. 75, 1201–1241 (2003)
Sachdev, S. Colloquium: order and quantum phase transitions in the cuprate superconductors. Rev. Mod. Phys. 75, 913–932 (2003)
Vojta, M. Lattice symmetry breaking in cuprate superconductors: stripes, nematics, and superconductivity. Adv. Phys. 58, 699–820 (2009)
Kim, E.-A. et al. Theory of the nodal nematic quantum phase transition in superconductors. Phys. Rev. B 77, 184514 (2008)
Fradkin, E., Kivelson, S. A., Lawler, M. J., Eisenstein, J. P. & Mackenzie, A. P. Nematic Fermi fluids in condensed matter physics. Annu. Rev. Condens. Matter Phys. 1, 7.1–7.26 (2010)
Cvetkovic, V., Nussinov, Z., Mukhin, S. & Zaanen, J. Observing the fluctuating stripes in high-Tc superconductors. Europhys. Lett. 81, 27001 (2008)
Borzi, R. A. et al. Formation of a nematic fluid at high fields in Sr3Ru2O7 . Science 315, 214–217 (2007)
Chuang, T.-M. et al. Nematic electronic structure in the “parent” state of the iron-based superconductor Ca(Fe1-xCox)2As2 . Science 327, 181–184 (2010)
Raghu, S. et al. Microscopic theory of the nematic phase in Sr3Ru2O7 . Phys. Rev. B 79, 214402 (2009)
Lv, W., Wu, J. & Phillips, P. Orbital ordering induces structural phase transition and the resistivity anomaly in iron pnictides. Phys. Rev. B 80, 224506 (2009)
Lee, W.-C. & Wu, C. Theory of unconventional metamagnetic electron states in orbital band systems. Phys. Rev. B 80, 104438 (2009)
Krüger, F., Kumar, S., Zaanen, J. & van den Brink, J. Spin-orbital frustrations and anomalous metallic state in iron-pnictide superconductors. Phys. Rev. B 79, 054504 (2009)
Kaminski, A. et al. Spontaneous breaking of time-reversal symmetry in the pseudogap state of a high-T c superconductor. Nature 416, 610–613 (2002)
Fauqué, B. et al. Magnetic order in the pseudogap phase of high-Tc superconductors. Phys. Rev. Lett. 96, 197001 (2006)
Li, Y. et al. Unusual magnetic order in the pseudogap region of the superconductor HgBa2CuO4+δ . Nature 455, 372–375 (2008)
Sun, X. F., Segawa, K. & Ando, Y. Metal-to-insulator crossover in YBa2Cu3Oy probed by low-temperature quasiparticle heat transport. Phys. Rev. Lett. 93, 107001 (2004)
Daou, R. et al. Broken rotational symmetry in the pseudogap phase of a high-Tc superconductor. Nature 463, 519–522 (2010)
Hinkov, V. et al. Electronic liquid crystal state in the high-temperature superconductor YBa2Cu3O6. 45 . Science 319, 597–600 (2008)
Sun, K., Lawler, M. J. & Kim, E.-A. Spin-charge interplay in electronic liquid crystals: fluctuating spin stripe driven by charge nematic. Phys. Rev. Lett. 104, 106405 (2010)
Acknowledgements
We are grateful to P. Abbamonte, D. Bonn, J.C. Campuzano, D.M. Eigler, E. Fradkin, T. Hanaguri, W. Hardy, J. E. Hoffman, S. Kivelson, A.P. Mackenzie, M. Norman, B. Ramshaw, S. Sachdev, G. Sawatzky, H. Takagi, J. Tranquada and J. Zaanen, for discussions and communications. Theoretical studies were supported by NSF DMR-0520404 to the Cornell Center for Materials Research. Experimental studies are supported by the Center for Emergent Superconductivity, an Energy Frontier Research Center, headquartered at Brookhaven National Laboratory and funded by the US Department of Energy, under DE-2009-BNL-PM015, as well as by a Grant-in-Aid for Scientific Research from the Ministry of Science and Education (Japan) and the Global Centers of Excellence Program for Japan Society for the Promotion of Science. A.R.S. acknowledges support from the US Army Research Office. M.J.L., J.C.D. and E.-A.K. thank KITP for its hospitality. J.C.D. acknowledges gratefully the hospitality and support of the Physics and Astronomy Department at the University of British Columbia, Vancouver, Canada.
Author information
Authors and Affiliations
Contributions
M.J.L. and E.-A.K. led the theoretical studies and initially observed the possibility of nematic order in electronic structure images; M.J.L., K.F. and J.P.S. developed the data analysis algorithms and carried out the analysis; K.F., J.L., C.K.K., A.R.S. and Y.K. carried out the experiments and systematic tests; K.F, H.E. and S.U. synthesized the sequence of samples; K.F. was responsible for the figures and SOM; E.-A.K., J.C.D. and M.J.L. supervised the investigation and wrote the paper. The manuscript reflects the contributions of all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
This file contains Supplementary Notes and Data 1-6, Supplementary Figures S1-S6 with legends, and a table showing a list of symbols. (PDF 8808 kb)
Supplementary Movie 1
This movie shows the reduced energy (e) dependence of coarse-grained r-space nematic order parameter ONQ(r,e). The procedure for generating the map of ONQ(r,e) for a given value of e is explained in section VI of the Supplementary Information file (Equation S10) . The movie is referred to in paragraph 12 of the main text. (MOV 141 kb)
Supplementary Movie 2
This movie shows the reduced energy (e) dependence of coarse-grained r-space nematic order parameter OSQ(r,e). The procedure for generating the map of ONQ(r,e) for a given value of e is explained in section VI of the Supplementary Information file (Equation S11). The movie is referred to in paragraph 12 of the main text. (MOV 226 kb)
Rights and permissions
About this article
Cite this article
Lawler, M., Fujita, K., Lee, J. et al. Intra-unit-cell electronic nematicity of the high-Tc copper-oxide pseudogap states. Nature 466, 347–351 (2010). https://doi.org/10.1038/nature09169
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature09169
This article is cited by
-
Discovery of orbital ordering in Bi2Sr2CaCu2O8+x
Nature Materials (2024)
-
Atomically precise engineering of spin–orbit polarons in a kagome magnetic Weyl semimetal
Nature Communications (2024)
-
Non-trivial band topology and orbital-selective electronic nematicity in a titanium-based kagome superconductor
Nature Physics (2023)
-
Unidirectional electron–phonon coupling in the nematic state of a kagome superconductor
Nature Physics (2023)
-
Pair density wave state in a monolayer high-Tc iron-based superconductor
Nature (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.