Abstract
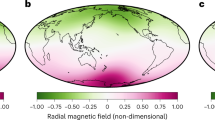
The magnetic field inside the Earth’s fluid and electrically conducting outer core cannot be directly probed. The root-mean-squared (r.m.s.) intensity for the resolved part of the radial magnetic field at the core–mantle boundary is 0.3 mT, but further assumptions are needed to infer the strength of the field inside the core. Recent diagnostics obtained from numerical geodynamo models1 indicate that the magnitude of the dipole field at the surface of a fluid dynamo is about ten times weaker than the r.m.s. field strength in its interior, which would yield an intensity of the order of several millitesla within the Earth’s core. However, a 60-year signal found in the variation in the length of day2 has long been associated with magneto-hydrodynamic torsional waves carried by a much weaker internal field3,4. According to these studies, the r.m.s. strength of the field in the cylindrical radial direction (calculated for all length scales) is only 0.2 mT, a figure even smaller than the r.m.s. strength of the large-scale (spherical harmonic degree n ≤ 13) field visible at the core–mantle boundary. Here we reconcile numerical geodynamo models with studies of geostrophic motions in the Earth’s core that rely on geomagnetic data. From an ensemble inversion of core flow models, we find a torsional wave recurring every six years, the angular momentum of which accounts well for both the phase and the amplitude of the six-year signal for change in length of day detected over the second half of the twentieth century5. It takes about four years for the wave to propagate throughout the fluid outer core, and this travel time translates into a slowness for Alfvén waves that corresponds to a r.m.s. field strength in the cylindrical radial direction of approximately 2 mT. Assuming isotropy, this yields a r.m.s. field strength of 4 mT inside the Earth’s core.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



 exceeds 2–3 mT in most of the fluid domain outside the tangent cylinder, except towards the Equator, where it reaches values close to what is observed at the CMB.
exceeds 2–3 mT in most of the fluid domain outside the tangent cylinder, except towards the Equator, where it reaches values close to what is observed at the CMB.

Similar content being viewed by others
References
Aubert, J., Labrosse, S. & Poitou, C. Modelling the palaeo-evolution of the geodynamo. Geophys. J. Int. 179, 1414–1428 (2009)
Roberts, P. H., Yu, Z. J. & Russel, C. T. On the 60-year signal from the core. Geophys. Astrophys. Fluid Dyn. 101, 11–35 (2007)
Zatman, S. & Bloxham, J. Torsional oscillations and the magnetic field within the Earth’s core. Nature 388, 760–763 (1997)
Buffett, B. A., Mound, J. & Jackson, A. Inversion of torsional oscillations for the structure and dynamics of Earth's core. Geophys. J. Int. 177, 878–890 (2009)
Abarca del Rio, R., Gambis, D. & Salstein, D. A. Interannual signals in length of day and atmospheric angular momentum. Ann. Geophys. 18, 347–364 (2000)
Gillet, N., Pais, M. A. & Jault, D. Ensemble inversion of time-dependent core flow models. Geochem. Geophys. Geosyst. 10 Q06004 10.1029/2008GC002290 (2009)
Pais, M. A. & Jault, D. Quasi-geostrophic flows responsible for the secular variation of the Earth's magnetic field. Geophys. J. Int. 173, 421–443 (2008)
Jault, D. Axial invariance of rapidly varying diffusionless motions in the Earth's core interior. Phys. Earth Planet. Inter. 166, 67–76 (2008)
Alfvén, H. Existence of electromagnetic-hydrodynamic waves. Nature 150, 405–406 (1942)
Jault, D., Gire, C. & Le Mouël, J.-L. Westward drift, core motions and exchanges of angular momentum between core and mantle. Nature 333, 353–356 (1988)
Jackson, A., Bloxham, J. & Gubbins, D. in Dynamics of the Earth's Deep Interior and Earth Rotation (eds LeMouël, J.-L. Smylie, D. E. & Herring, T. A.) Vol. 72 97–107 (American Geophysical Union, 1993)
Jackson, A., Jonkers, A. R. T. & Walker, M. R. Four centuries of geomagnetic secular variation from historical records. Phil. Trans. R. Soc. Lond. A 358, 957–990 (2000)
Gross, R. S. A combined length-of-day series spanning 1832–1977: LUNAR97. Phys. Earth Planet. Inter. 123, 65–76 (2001)
Jackson, A. Time-dependency of tangentially geostrophic core surface motions. Phys. Earth Planet. Inter. 103, 293–311 (1997)
Pais, M. A., Oliveira, O. & Nogueira, F. Nonuniqueness of inverted core-mantle boundary flows and deviation from tangential geostrophy. J. Geophys. Res. 109 B08105 10.1029/2004JB003012 (2004)
Bloxham, J., Zatman, S. & Dumberry, M. The origin of geomagnetic jerks. Nature 420, 65–68 (2002)
Mound, J. E. & Buffett, B. Detection of a gravitational oscillation in length of day. Earth Planet. Sci. Lett. 243, 383–389 (2006)
Jordi, C., Morrison, L. V., Rosen, R. D., Salstein, D. A. & Rosselló, G. Fluctuations in the Earth's rotation since 1830 from high-resolution astronomical data. Geophys. J. Int. 117, 811–818 (1994)
Braginsky, S. I. Torsional magnetohydrodynamic vibrations in the Earth's core and variations in day length. Geomagn. Aeron. 10, 1–8 (1970)
Fournier, A., Eymin, C. & Alboussière, T. A case for variational geomagnetic data assimilation: insights from a one-dimensional, nonlinear and sparsely observed MHD system. Nonlinear Process. Geophys. 14, 1–18 (2007)
Canet, E., Fournier, A. & Jault, D. Forward and adjoint quasi-geostrophic models of the geomagnetic secular variation. J. Geophys. Res. 114 B11101 10.1029/2008JB006189 (2009)
Buffett, B. A., Mathews, P. M. & Herring, T. A. Modeling of nutation and precession: effects of electromagnetic coupling. J. Geophys. Res. 107 (B4). 2070 10.1029/2000JB000056 (2002)
Jackson, A. & Livermore, P. On Ohmic heating in the Earth's core. I: Nutation constraints. Geophys. J. Int. 10.1111/j.1365–246X.2008.04008.x (2009)
Dumberry, M. & Mound, J. E. Constraints on core-mantle electromagnetic coupling from torsional oscillation normal modes. J. Geophys. Res. 113 10.1029/2007JB005135 (2008)
Ohta, K. et al. Electrical conductivities of pyrolitic mantle and MORB materials up to the lowermost mantle conditions. Earth Planet. Sci. Lett. 289, 497–502 (2010)
Zhang, J., Richards, P. G. & Schaff, D. P. Wide-scale detection of earthquake waveform doublets and further evidence for inner core super-rotation. Geophys. J. Int. 174, 993–1006 (2008)
Taylor, J. B. The magneto-hydrodynamics of a rotating fluid and the Earth's dynamo problem. Proc. R. Soc. Lond. A 274, 274–283 (1963)
Rhines, P. B. Waves and turbulence on a beta-plane. J. Fluid Mech. 122, 417–443 (1975)
Olsen, N. & Mandea, M. Rapidly changing flows in the Earth's core. Nature Geosci. 1, 390–394 (2008)
Friis-Christensen, E., Lühr, H. & Hulot, G. Swarm: a constellation to study the Earth's magnetic field. Earth Planets Space 58, 351–358 (2006)
Acknowledgements
We thank M. Dumberry and P. Roberts for discussions. We also thank A. Jackson, who helped improve the quality of the manuscript. N.G. was funded by a grant from the French Agence Nationale de la Recherche, Research program VS-QG (grant number BLAN06-2.155316). The IPGP contribution number for A.F. is 2618. The study has also been supported in part by the French Centre National d'Etudes Spatiales.
Author information
Authors and Affiliations
Contributions
The ensemble core flow inversions, data analysis and error covariances were carried out by NG. The ΔLOD time series analysis was performed by N.G. and D.J. E.C. and A.F. developed the torsional wave variational data assimilation code; runs were performed by N.G. and E.C. The manuscript was mainly written by N.G. and D.J., with a little help from A.F. D.J. played an important part in the discussion of the theoretical background.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
This file contains Supplementary Data, Supplementary Figures 1-3 with legends and References. (PDF 202 kb)
Rights and permissions
About this article
Cite this article
Gillet, N., Jault, D., Canet, E. et al. Fast torsional waves and strong magnetic field within the Earth’s core. Nature 465, 74–77 (2010). https://doi.org/10.1038/nature09010
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature09010
This article is cited by
-
Inner core static tilt inferred from intradecadal oscillation in the Earth’s rotation
Nature Communications (2023)
-
Jupiter’s cloud-level variability triggered by torsional oscillations in the interior
Nature Astronomy (2023)
-
Sustaining Earth’s magnetic dynamo
Nature Reviews Earth & Environment (2022)
-
Core Eigenmodes and their Impact on the Earth’s Rotation
Surveys in Geophysics (2022)
-
Gravity Variations and Ground Deformations Resulting from Core Dynamics
Surveys in Geophysics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.