Abstract
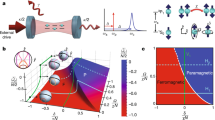
A phase transition describes the sudden change of state of a physical system, such as melting or freezing. Quantum gases provide the opportunity to establish a direct link between experiments and generic models that capture the underlying physics. The Dicke model describes a collective matter–light interaction and has been predicted to show an intriguing quantum phase transition. Here we realize the Dicke quantum phase transition in an open system formed by a Bose–Einstein condensate coupled to an optical cavity, and observe the emergence of a self-organized supersolid phase. The phase transition is driven by infinitely long-range interactions between the condensed atoms, induced by two-photon processes involving the cavity mode and a pump field. We show that the phase transition is described by the Dicke Hamiltonian, including counter-rotating coupling terms, and that the supersolid phase is associated with a spontaneously broken spatial symmetry. The boundary of the phase transition is mapped out in quantitative agreement with the Dicke model. Our results should facilitate studies of quantum gases with long-range interactions and provide access to novel quantum phases.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Anderson, M. H., Ensher, J. R., Matthews, M. R., Wieman, C. E. & Cornell, E. A. Observation of Bose-Einstein condensation in a dilute atomic vapor. Science 269, 198–201 (1995)
Davis, K. B. et al. Bose-Einstein condensation in a gas of sodium atoms. Phys. Rev. Lett. 75, 3969–3973 (1995)
Regal, C. A., Greiner, M. & Jin, D. S. Observation of resonance condensation of fermionic atom pairs. Phys. Rev. Lett. 92, 040403 (2004)
Zwierlein, M. W. et al. Condensation of pairs of fermionic atoms near a Feshbach resonance. Phys. Rev. Lett. 92, 120403 (2004)
Bartenstein, M. et al. Collective excitations of a degenerate gas at the BEC-BCS crossover. Phys. Rev. Lett. 92, 203201 (2004)
Greiner, M., Mandel, O., Esslinger, T., Hänsch, T. W. & Bloch, I. Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature 415, 39–44 (2002)
Feynman, R. P. Simulating physics with computers. Int. J. Theor. Phys. 21, 467–488 (1982)
Lloyd, S. Universal quantum simulators. Science 273, 1073–1078 (1996)
Lahaye, T., Menotti, C., Santos, L., Lewenstein, M. & Pfau, T. The physics of dipolar bosonic quantum gases. Rep. Prog. Phys. 72, 126401 (2009)
Asbóth, J. K., Domokos, P. & Ritsch, H. Correlated motion of two atoms trapped in a single-mode cavity field. Phys. Rev. A 70, 013414 (2004)
Asbóth, J. K., Ritsch, H. & Domokos, P. Collective excitations and instability of an optical lattice due to unbalanced pumping. Phys. Rev. Lett. 98, 203008 (2007)
Domokos, P. & Ritsch, H. Collective cooling and self-organization of atoms in a cavity. Phys. Rev. Lett. 89, 253003 (2002)
Nagy, D., Szirmai, G. & Domokos, P. Self-organization of a Bose-Einstein condensate in an optical cavity. Eur. Phys. J. D 48, 127–137 (2008)
Black, A. T., Chan, H. W. & Vuletić, V. Observation of collective friction forces due to spatial self-organization of atoms: from Rayleigh to Bragg scattering. Phys. Rev. Lett. 91, 203001 (2003)
Inouye, S. et al. Superradiant Rayleigh scattering from a Bose-Einstein condensate. Science 285, 571–574 (1999)
Yoshikawa, Y., Torii, Y. & Kuga, T. Superradiant light scattering from thermal atomic vapors. Phys. Rev. Lett. 94, 083602 (2005)
Slama, S., Bux, S., Krenz, G., Zimmermann, C. & Courteille, P. W. Superradiant Rayleigh scattering and collective atomic recoil lasing in a ring cavity. Phys. Rev. Lett. 98, 053603 (2007)
Bonifacio, R. & De Salvo, L. Collective atomic recoil laser (CARL) optical gain without inversion by collective atomic recoil and self-bunching of two-level atoms. Nucl. Instrum. Methods 341, 360–362 (1994)
Sachdev, S. Quantum Phase Transitions (Cambridge Univ. Press, 1999)
Amico, L., Fazio, R., Osterloh, A. & Vedral, V. Entanglement in many-body systems. Rev. Mod. Phys. 80, 517–576 (2008)
Osterloh, A., Amico, L., Falci, G. & Fazio, R. Scaling of entanglement close to a quantum phase transition. Nature 416, 608–610 (2002)
Botet, R., Jullien, R. & Pfeuty, P. Size scaling for infinitely coordinated systems. Phys. Rev. Lett. 49, 478–481 (1982)
Dicke, R. H. Coherence in spontaneous radiation processes. Phys. Rev. 93, 99–110 (1954)
Hepp, K. & Lieb, E. H. On the superradiant phase transition for molecules in a quantized radiation field: the Dicke maser model. Ann. Phys. 76, 360–404 (1973)
Wang, Y. K. & Hioe, F. T. Phase transition in the Dicke model of superradiance. Phys. Rev. A 7, 831–836 (1973)
Dimer, F., Estienne, B., Parkins, A. S. & Carmichael, H. J. Proposed realization of the Dicke-model quantum phase transition in an optical cavity QED system. Phys. Rev. A 75, 013804 (2007)
Andreev, A. F. & Lifshitz, I. M. Quantum theory of crystal defects. Sov. Phys. JETP 56, 2057–2068 (1969)
Chester, G. V. Speculations on Bose-Einstein condensation and quantum crystals. Phys. Rev. A 2, 256–258 (1970)
Leggett, A. J. Can a solid be “superfluid”? Phys. Rev. Lett. 25, 1543–1546 (1970)
Büchler, H. P. & Blatter, G. Supersolid versus phase separation in atomic Bose-Fermi mixtures. Phys. Rev. Lett. 91, 130404 (2003)
Maschler, C., Mekhov, I. B. & Ritsch, H. Ultracold atoms in optical lattices generated by quantized light fields. Eur. Phys. J. D 46, 545–560 (2008)
Domokos, P. & Ritsch, H. Mechanical effects of light in optical resonators. J. Opt. Soc. Am. B 20, 1098–1130 (2003)
Gopalakrishnan, S., Lev, B. L. & Goldbart, P. M. Emergent crystallinity and frustration with Bose-Einstein condensates in multimode cavities. Nature Phys. 5, 845–850 (2009)
Murch, K. W., Moore, K. L., Gupta, S. & Stamper-Kurn, D. M. Observation of quantum-measurement backaction with an ultracold atomic gas. Nature Phys. 4, 561–564 (2008)
Orzel, C., Tuchman, A. K., Fenselau, M. L., Yasuda, M. & Kasevich, M. A. Squeezed states in a Bose-Einstein condensate. Science 291, 2386–2389 (2001)
Brennecke, F., Ritter, S., Donner, T. & Esslinger, T. Cavity optomechanics with a Bose-Einstein condensate. Science 322, 235–238 (2008)
Nagy, D., Asboth, J. K., Domokos, P. & Ritsch, H. Self-organization of a laser-driven cold gas in a ring cavity. Europhys. Lett. 74, 254–260 (2006)
Asbóth, J. K., Domokos, P., Ritsch, H. & Vukics, A. Self-organization of atoms in a cavity field: threshold, bistability, and scaling laws. Phys. Rev. A 72, 053417 (2005)
Lambert, N., Emary, C. & Brandes, T. Entanglement and the phase transition in single-mode superradiance. Phys. Rev. Lett. 92, 073602 (2004)
Vidal, J. & Dusuel, S. Finite-size scaling exponents in the Dicke model. Europhys. Lett. 74, 817–822 (2006)
Maschler, C., Ritsch, H., Vukics, A. & Domokos, P. Entanglement assisted fast reordering of atoms in an optical lattice within a cavity at T = 0. Opt. Commun. 273, 446–450 (2007)
Mekhov, I. B., Maschler, C. & Ritsch, H. Probing quantum phases of ultracold atoms in optical lattices by transmission spectra in cavity quantum electrodynamics. Nature Phys. 3, 319–323 (2007)
Mekhov, I. B. & Ritsch, H. Quantum nondemolition measurements and state preparation in quantum gases by light detection. Phys. Rev. Lett. 102, 020403 (2009)
Öttl, A., Ritter, S., Köhl, M. & Esslinger, T. Hybrid apparatus for Bose-Einstein condensation and cavity quantum electrodynamics: single atom detection in quantum degenerate gases. Rev. Sci. Instrum. 77, 063118 (2006)
Brennecke, F. et al. Cavity QED with a Bose–Einstein condensate. Nature 450, 268–271 (2007)
Pitaevskii, L. & Stringari, S. Bose-Einstein Condensation 161–176 (Oxford Univ. Press, 2003)
Nagy, D., Kónya, G., Szirmai, G. & Domokos, P. Dicke-model phase transition in the quantum motion of a Bose-Einstein condensate in an optical cavity. Phys. Rev. Lett. 104, 130401 (2010)
Greiner, M., Bloch, I., Mandel, O., Hänsch, T. W. & Esslinger, T. Exploring phase coherence in a 2D lattice of Bose-Einstein condensates. Phys. Rev. Lett. 87, 160405 (2001)
Acknowledgements
We thank G. Blatter, I. Carusotto, P. Domokos, A. Imamoglu, S. Leinss, R. Mottl, L. Pollet, H. Ritsch and M. Troyer for discussions. Financial funding from NAME-QUAM (European Commission Seventh Framework Programme Future and Emerging Technologies Open Scheme, grant number 225187) and QSIT (ETH Zürich) is acknowledged. C.G. acknowledges support from an ETH Fellowship.
Author information
Authors and Affiliations
Contributions
The data was taken and analysed by K.B. and C.G. The theoretical analysis was mainly performed by F.B. and T.E. The relation to the Dicke model was realized by F.B. The experimental concept was developed by T.E. All authors contributed extensively to the discussion of the results as well as to the preparation of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Baumann, K., Guerlin, C., Brennecke, F. et al. Dicke quantum phase transition with a superfluid gas in an optical cavity. Nature 464, 1301–1306 (2010). https://doi.org/10.1038/nature09009
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature09009
This article is cited by
-
Sudden change of the photon output field marks phase transitions in the quantum Rabi model
Communications Physics (2024)
-
Experimental observation of spontaneous symmetry breaking in a quantum phase transition
Science China Physics, Mechanics & Astronomy (2024)
-
Density-wave ordering in a unitary Fermi gas with photon-mediated interactions
Nature (2023)
-
Supersolidity in ultracold dipolar gases
Nature Reviews Physics (2023)
-
Engineering random spin models with atoms in a high-finesse cavity
Nature Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.