Abstract
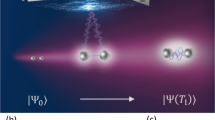
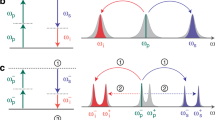
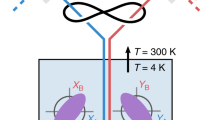
Entangled systems display correlations that are stronger than can be obtained classically. This makes entanglement an essential resource for a number of applications, such as quantum information processing, quantum computing and quantum communications1,2. The ability to control the transfer of entanglement between different locations will play a key role in these quantum protocols and enable quantum networks3. Such a transfer requires a system that can delay quantum correlations without significant degradation, effectively acting as a short-term quantum memory. An important benchmark for such systems is the ability to delay Einstein–Podolsky–Rosen (EPR) levels of entanglement and to be able to tune the delay. EPR entanglement is the basis for a number of quantum protocols, allowing the remote inference of the properties of one system (to better than its standard quantum limit) through measurements on the other correlated system. Here we show that a four-wave mixing process based on a double-lambda scheme in hot 85Rb vapour allows us to obtain an optically tunable delay for EPR entangled beams of light. A significant maximum delay, of the order of the width of the cross-correlation function, is achieved. The four-wave mixing also preserves the quantum spatial correlations of the entangled beams. We take advantage of this property to delay entangled images, making this the first step towards a quantum memory for images4.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



 ’ symbol.
’ symbol.

Similar content being viewed by others
References
Galindo, A. & Martin-Delgado, M. A. Information and computation: Classical and quantum aspects. Rev. Mod. Phys. 74, 347–423 (2002)
Braunstein, S. L. & van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 77, 513–577 (2005)
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008)
Vasilyev, D. V., Sokolov, I. V. & Polzik, E. S. Quantum memory for images: A quantum hologram. Phys. Rev. A 77, 020302(R) (2008)
Hau, L. V., Harris, S. E., Dutton, Z. & Behroozi, C. H. Light speed reduction to 17 metres per second in an ultracold atomic gas. Nature 397, 594–598 (1999)
Camacho, R. M., Pack, M. V., Howell, J. C., Schweinsberg, A. & Boyd, R. W. Wide-bandwidth, tunable, multiple-pulse-width optical delays using slow light in cesium vapor. Phys. Rev. Lett. 98, 153601 (2007)
Boyer, V., McCormick, C. F., Arimondo, E. & Lett, P. D. Ultraslow propagation of matched pulses by four-wave mixing in an atomic vapor. Phys. Rev. Lett. 99, 143601 (2007)
Broadbent, C. J., Camacho, R. M., Xin, R. & Howell, J. C. Preservation of energy-time entanglement in a slow light medium. Phys. Rev. Lett. 100, 133602 (2008)
Chaneliere, T. et al. Storage and retrieval of single photons transmitted between remote quantum memories. Nature 438, 833–836 (2005)
Eisaman, M. D. et al. Electromagnetically induced transparency with tunable single-photon pulses. Nature 438, 837–841 (2005)
Choi, K. S., Deng, H., Laurat, J. & Kimble, H. J. Mapping photonic entanglement into and out of a quantum memory. Nature 452, 67–71 (2008)
Akamatsu, D. et al. Ultraslow propagation of squeezed vacuum pulses with electromagnetically induced transparency. Phys. Rev. Lett. 99, 153602 (2007)
Honda, K. et al. Storage and retrieval of a squeezed vacuum. Phys. Rev. Lett. 100, 093601 (2008)
Appel, J., Figueroa, E., Korystov, D., Lobino, M. & Lvovsky, A. I. Quantum memory for squeezed light. Phys. Rev. Lett. 100, 093602 (2008)
Hétet, G. et al. Delay of squeezing and entanglement using electromagnetically induced transparency in a vapour cell. Opt. Express 16, 7369–7381 (2008)
Duan, L. M., Giedke, G., Cirac, J. I. & Zoller, P. Inseparability criterion for continuous variable systems. Phys. Rev. Lett. 84, 2722–2725 (2000)
Reid, M. D. Demonstration of the Einstein-Podolsky-Rosen paradox using nondegenerate parametric amplification. Phys. Rev. A 40, 913–923 (1989)
McCormick, C. F., Marino, A. M., Boyer, V. & Lett, P. D. Strong low-frequency quantum correlations from a four-wave-mixing amplifier. Phys. Rev. A 78, 043816 (2008)
Boyer, V., Marino, A. M., Pooser, R. C. & Lett, P. D. Entangled images from four-wave mixing. Science 321, 544–547 (2008)
Ou, Z. Y., Pereira, S. F., Kimble, H. J. & Peng, K. C. Realization of the Einstein-Podolsky-Rosen paradox for continuous-variables. Phys. Rev. Lett. 68, 3663–3666 (1992)
Bowen, W. P., Schnabel, R., Lam, P. K. & Ralph, T. C. Experimental characterization of continuous-variable entanglement. Phys. Rev. A 69, 012304 (2004)
Weedbrook, C., Grosse, N. B., Symul, T., Lam, P. K. & Ralph, T. C. Quantum cloning of continuous-variable entangled states. Phys. Rev. A 77, 052313 (2008)
Tan, S. M. Confirming entanglement in continuous variable quantum teleportation. Phys. Rev. A 60, 2752–2758 (1999)
Grosshans, F. & Grangier, P. Quantum cloning and teleportation criteria for continuous quantum variables. Phys. Rev. A 64, 010301(R) (2001)
Boyd, R. W., Gauthier, D. J., Gaeta, A. L. & Willner, A. E. Maximum time delay achievable on propagation through a slow-light medium. Phys. Rev. A 71, 023801 (2005)
Vudyasetu, P. K., Camacho, R. M. & Howell, J. C. Storage and retrieval of multimode transverse images in hot atomic rubidium vapor. Phys. Rev. Lett. 100, 123903 (2008)
Shuker, M., Firstenberg, O., Pugatch, R., Ron, A. & Davidson, N. Storing images in warm atomic vapor. Phys. Rev. Lett. 100, 223601 (2008)
Boyer, V., Marino, A. M. & Lett, P. D. Generation of spatially broadband twin beams for quantum imaging. Phys. Rev. Lett. 100, 143601 (2008)
Collins, O. A., Jenkins, S. D., Kuzmich, A. & Kennedy, T. A. B. Multiplexed memory insensitive quantum repeaters. Phys. Rev. Lett. 98, 060502 (2007)
Tordrup, K., Negretti, A. & Molmer, K. Holographic quantum computing. Phys. Rev. Lett. 101, 040501 (2008)
Acknowledgements
R.C.P. is supported by the Intelligence Community Postdoctoral Program.
Author information
Authors and Affiliations
Corresponding author
Supplementary information
Supplementary Information
This file contains Supplementary Notes, Supplementary Figures 1-2 with Legends and a Supplementary Reference (PDF 198 kb)
Rights and permissions
About this article
Cite this article
Marino, A., Pooser, R., Boyer, V. et al. Tunable delay of Einstein–Podolsky–Rosen entanglement. Nature 457, 859–862 (2009). https://doi.org/10.1038/nature07751
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature07751
This article is cited by
-
Quantum squeezing enhancement based on phase-sensitive cascaded four-wave mixing processes
Science China Physics, Mechanics & Astronomy (2023)
-
Controllable atom-photon entanglement via quantum interference near plasmonic nanostructure
Scientific Reports (2022)
-
Generation of enhanced entanglement of directly and indirectly coupled modes in a two-cavity magnomechanical system
Quantum Information Processing (2022)
-
Creating heralded hyper-entangled photons using Rydberg atoms
Light: Science & Applications (2021)
-
Orbital angular momentum multiplexed deterministic all-optical quantum teleportation
Nature Communications (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.