Abstract
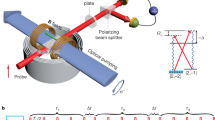
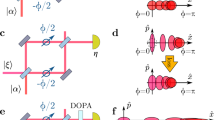
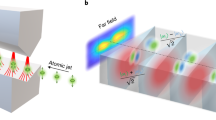
Quantum mechanics places a fundamental limit on the accuracy of measurements. In most circumstances, the measurement uncertainty is distributed equally between pairs of complementary properties; this leads to the ‘standard quantum limit’ for measurement resolution. Using a technique known as ‘squeezing’, it is possible to reduce the uncertainty of one desired property below the standard quantum limit at the expense of increasing that of the complementary one. Squeezing is already being used to enhance the sensitivity of gravity-wave detectors1 and may play a critical role in other high precision applications, such as atomic clocks2 and optical communications3. Spin squeezing (the squeezing of angular momentum variables) is a powerful tool, particularly in the context of quantum light–matter interfaces4,5,6,7,8,9. Although impressive gains in squeezing have been made, optical spin-squeezed systems are still many orders of magnitude away from the maximum possible squeezing, known as the Heisenberg uncertainty limit. Here we demonstrate how an optical system can be squeezed essentially all the way to this fundamental bound. We construct spin-squeezed states by overlapping three indistinguishable photons in an optical fibre and manipulating their polarization (spin), resulting in the formation of a squeezed composite particle known as a ‘triphoton’. The symmetry properties of polarization imply that the measured triphoton states can be most naturally represented by quasi-probability distributions on the surface of a sphere. In this work we show that the spherical topology of polarization imposes a limit on how much squeezing can occur, leading to the quasi-probability distributions wrapping around the sphere—a phenomenon we term ‘over-squeezing’. Our observations of spin-squeezing in the few-photon regime could lead to new quantum resources for enhanced measurement, lithography and information processing that can be precisely engineered photon-by-photon.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout


 and
and
 for 11 squeezed triphoton states.
for 11 squeezed triphoton states.

Similar content being viewed by others
References
Goda, K. et al. A quantum-enhanced prototype gravitational-wave detector. Nature Phys. 4, 472–476 (2008)
Ye, J., Kimble, H. & Katori, H. Quantum state engineering and precision metrology using state-insensitive light traps. Science 320, 1734–1738 (2008)
Furusawa, A. et al. Unconditional quantum teleportation. Science 282, 706–709 (1998)
Hald, J., Sørensen, J. & Polzik, E. Spin squeezed atoms: A macroscopic entangled ensemble created by light. Phys. Rev. Lett. 83, 1319–1322 (1999)
Bowen, W., Schnabel, R., Bachor, H.-A. & Lam, P. Polarization squeezing of continuous variable Stokes parameters. Phys. Rev. Lett. 88, 093601 (2002)
Heersink, J. et al. Polarization squeezing of intense pulses with a fiber-optic Sagnac interferometer. Phys. Rev. A 68, 013815 (2003)
Marquardt, C. et al. Quantum reconstruction of an intense polarization squeezed optical state. Phys. Rev. Lett. 99, 220401 (2007)
Chaudhury, G. et al. Quantum control of the hyperfine spin of a Cs atom ensemble. Phys. Rev. Lett. 99, 163002 (2007)
Ghose, S. S., Stock, R., Jessen, P. S., Lal, R. & Silberfarb, A. Chaos, entanglement and decoherence in the quantum kicked top. Phys. Rev. A 78, 042318 (2008)
Agarwal, G. Relation between atomic coherent-state representation, state multipoles, and generalized phase-space distributions. Phys. Rev. A 24, 2889–2896 (1981)
Dowling, J., Agarwal, G. & Schleich, W. Wigner distribution of a general angular-momentum state: Applications to a collection of two-level atoms. Phys. Rev. A 49, 4101–4109 (1994)
Stratonovich, R. L. Gauge invariant generalization of Wigner distributions. Dokl. Akad. Nauk SSSR 109, 72–75 (1956)
Luis, A. Quantum polarization distributions via marginals of quadrature distributions. Phys. Rev. A 71, 053801 (2005)
Luis, A. Nonclassical polarization states. Phys. Rev. A 73, 063806 (2006)
Arecchi, F., Courtens, E., Gilmore, R. & Thomas, H. Atomic coherent states in quantum optics. Phys. Rev. A 6, 2211–2273 (1972)
Mitchell, M. W., Lundeen, J. S. & Steinberg, A. M. Super-resolving phase measurements with a multiphoton entangled state. Nature 429, 161–164 (2004)
Lee, H., Kok, P., Cerf, N. J. & Dowling, J. P. Linear optics and projective measurements alone suffice to create large photon-number path entanglement. Phys. Rev. A 65, 030101 (2002)
Fiurášek, J. Conditional generation of n-photon entangled states of light. Phys. Rev. A 65, 053818 (2002)
Adamson, R. B. A., Shalm, L. K., Mitchell, M. W. & Steinberg, A. M. Multiparticle state tomography: hidden differences. Phys. Rev. Lett. 98, 043601 (2007)
Adamson, R. B. A., Turner, P. S., Mitchell, M. W. & Steinberg, A. M. Detecting hidden differences via permutation symmetries. Phys. Rev. A 78, 033832 (2008)
Durkin, G. A. & Dowling, J. P. Local and global distinguishability in quantum interferometry. Phys. Rev. Lett. 99, 070801 (2007)
Dowling, J. Correlated input-port, matter-wave interferometer: Quantum-noise limits to the atom-laser gyroscope. Phys. Rev. A 57, 4736–4746 (1998)
Walther, P. et al. De Broglie wavelength of a non-local four-photon state. Nature 429, 158–161 (2004)
Nagata, T., Okamoto, R., O’Brien, J., Sasaki, K. & Takeuchi, S. Beating the standard quantum limit with four-entangled photons. Science 316, 726–729 (2007)
Ou, Z. Fundamental quantum limit in precision phase measurement. Phys. Rev. A 55, 2598–2609 (1997)
Resch, K. J. et al. Time-reversal and super-resolving phase measurements. Phys. Rev. Lett. 98, 223601 (2007)
Miranowicz, A. & Grudka, A. A comparative study of relative entropy of entanglement, concurrence and negativity. J. Opt. B 6, 542–548 (2004)
Peres, A. Separability criterion for density matrices. Phys. Rev. Lett. 77, 1413–1415 (1996)
Horodecki, M. Separability of mixed states: necessary and sufficient conditions. Phys. Lett. A 223, 1–8 (1996)
Takeuchi, S. Beamlike twin-photon generation by use of type II parametric downconversion. Opt. Lett. 26, 843–845 (2001)
Acknowledgements
We thank S. Ghose and P. Jessen for discussions. This work was supported by the Natural Sciences and Engineering Research Council of Canada, Ontario Centres of Excellence, Canadian Institute for Photonic Innovations, Quantum Works, and the Canadian Institute for Advanced Research.
Author information
Authors and Affiliations
Corresponding author
Supplementary information
Supplementary Information
This file contains Supplementary Methods and Data, a Supplementary Discussion, Supplementary Table 1 and Supplementary Figures 1-2 with Legends (PDF 376 kb)
Rights and permissions
About this article
Cite this article
Shalm, L., Adamson, R. & Steinberg, A. Squeezing and over-squeezing of triphotons. Nature 457, 67–70 (2009). https://doi.org/10.1038/nature07624
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature07624
This article is cited by
-
Assessment of image resolution improvement by phase-sensitive optical parametric amplification
Applied Physics B (2011)
-
Squeeze until it hurts
Nature (2009)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.