Abstract
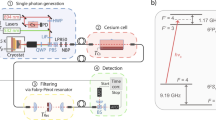
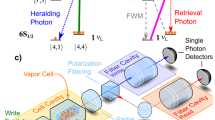
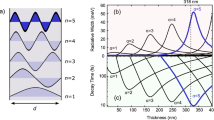
Coherent and reversible mapping of quantum information between light and matter is an important experimental challenge in quantum information science. In particular, it is an essential requirement for the implementation of quantum networks and quantum repeaters1,2,3. So far, quantum interfaces between light and atoms have been demonstrated with atomic gases4,5,6,7,8,9, and with single trapped atoms in cavities10. Here we demonstrate the coherent and reversible mapping of a light field with less than one photon per pulse onto an ensemble of ∼107 atoms naturally trapped in a solid. This is achieved by coherently absorbing the light field in a suitably prepared solid-state atomic medium11. The state of the light is mapped onto collective atomic excitations at an optical transition and stored for a pre-determined time of up to 1 μs before being released in a well-defined spatio-temporal mode as a result of a collective interference. The coherence of the process is verified by performing an interference experiment with two stored weak pulses with a variable phase relation. Visibilities of more than 95 per cent are obtained, demonstrating the high coherence of the mapping process at the single-photon level. In addition, we show experimentally that our interface makes it possible to store and retrieve light fields in multiple temporal modes. Our results open the way to multimode solid-state quantum memories as a promising alternative to atomic gases.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout

 = 0.5.
= 0.5.




Similar content being viewed by others
References
Briegel, H.-J., Dür, W., Cirac, J. I. & Zoller, P. Quantum repeaters: The role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932–5935 (1998)
Duan, L.-M., Lukin, M. D., Cirac, J. I. & Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418 (2001)
Simon, C. et al. Quantum repeaters with photon pair sources and multimode memories. Phys. Rev. Lett. 98, 190503 (2007)
Julsgaard, B., Sherson, J., Cirac, J. I., Fiurášek, J. & Polzik, E. S. Experimental demonstration of quantum memory for light. Nature 432, 482–486 (2004)
Chanelière, T. et al. Storage and retrieval of single photons transmitted between remote quantum memories. Nature 438, 833–836 (2005)
Eisaman, M. D. et al. Electromagnetically induced transparency with tunable single-photon pulses. Nature 438, 837–841 (2005)
Chou, C. W. et al. Measurement-induced entanglement for excitation stored in remote atomic ensembles. Nature 438, 828–832 (2005)
Honda, K. et al. Storage and retrieval of a squeezed vacuum. Phys. Rev. Lett. 100, 093601 (2008)
Appel, J., Figueroa, E., Korystov, D., Lobino, M. & Lvovsky, A. I. Quantum memory for squeezed light. Phys. Rev. Lett. 100, 093602 (2008)
Boozer, A. D., Boca, A., Miller, R., Northup, T. E. & Kimble, H. J. Reversible state transfer between light and a single trapped atom. Phys. Rev. Lett. 98, 193601 (2007)
Afzelius, M., Simon, C., de Riedmatten, H. & Gisin, N. Multimode quantum memory based on atomic frequency combs. Preprint at 〈http://arxiv.org/abs/0805.4164〉 (2008)
Fleischhauer, M. & Lukin, M. D. Dark-state polaritons in electromagnetically induced transparency. Phys. Rev. Lett. 84, 5094–5097 (2000)
Nunn, J. et al. Mapping broadband single-photon wave packets into an atomic memory. Phys. Rev. A 75, 011401 (2007)
Moiseev, S. A. & Kröll, S. Complete reconstruction of the quantum state of a single-photon wave packet absorbed by a Doppler-broadened transition. Phys. Rev. Lett. 87, 173601 (2001)
Kraus, B. et al. Quantum memory for nonstationary light fields based on controlled reversible inhomogeneous broadening. Phys. Rev. A 73, 020302 (2006)
Böttger, T., Thiel, C. W., Sun, Y. & Cone, R. L. Optical decoherence and spectral diffusion at 1.5 μm in Er3+Y2SiO5 versus magnetic field, temperature, and Er3+ concentration. Phys. Rev. B 73, 075101 (2006)
Fraval, E., Sellars, M. J. & Longdell, J. J. Dynamic decoherence control of a solid-state nuclear-quadrupole qubit. Phys. Rev. Lett. 95, 030506 (2005)
Longdell, J. J., Fraval, E., Sellars, M. J. & Manson, N. B. Stopped light with storage times greater than one second using electromagnetically induced transparency in a solid. Phys. Rev. Lett. 95, 063601 (2005)
Alexander, A. L., Longdell, J. J., Sellars, M. J. & Manson, N. B. Photon echoes produced by switching electric fields. Phys. Rev. Lett. 96, 043602 (2006)
Hétet, G., Longdell, J. J., Alexander, A. L., Lam, P. K. & Sellars, M. J. Electro-optic quantum memory for light using two-level atoms. Phys. Rev. Lett. 100, 023601 (2008)
Staudt, M. U. et al. Fidelity of an optical memory based on stimulated photon echoes. Phys. Rev. Lett. 98, 113601 (2007)
Staudt, M. U. et al. Interference of multimode photon echoes generated in spatially separated solid-state atomic ensembles. Phys. Rev. Lett. 99, 173602 (2007)
Ohlsson, N., Nilsson, M. & Kröll, S. Experimental investigation of delayed self-interference for single photons. Phys. Rev. A 68, 063812 (2003)
Hasegawa, Y. et al. Phase transfer in time-delayed interferometry with nuclear resonant scattering. Phys. Rev. Lett. 75, 2216–2219 (1995)
Mitsunaga, M., Yano, R. & Uesugi, N. Spectrally programmed stimulated photon echo. Opt. Lett. 16, 264–266 (1991)
Hastings-Simon, S. R. et al. Spectral hole burning spectroscopy in Nd3+:YVO4 . Phys. Rev. B 77, 125111 (2008)
Hesselink, W. H. & Wiersma, D. A. Picosecond photon echoes stimulated from an accumulated grating. Phys. Rev. Lett. 43, 1991–1994 (1979)
Rippe, L., Julsgaard, B., Walther, A., Ying, Y. & Kröll, S. Experimental quantum-state tomography of a solid-state qubit. Phys. Rev. A 77, 022307 (2008)
de Seze, F., Lavielle, V., Lorgeré, I. & Le Gouët, J. L. Chirped pulse generation of a narrow absorption line in a Tm3+:YAG crystal. Opt. Commun. 223, 321–330 (2003)
Gorshkov, A. V., André, A., Fleischhauer, M., Sørensen, A. S. & Lukin, M. D. Universal approach to optimal photon storage in atomic media. Phys. Rev. Lett. 98, 123601 (2007)
Acknowledgements
We thank E. Cavalli and M. Bettinelli for kindly lending us the Nd:YVO4 crystal. This work was supported by the Swiss NCCR Quantum Photonics and by the European Commission under the Integrated Project Qubit Applications.
Author information
Authors and Affiliations
Corresponding author
Supplementary information
Supplementary Information
This file contains Supplementary Data including Supplementary Figures 1-3 with Legends and a Supplementary Reference (PDF 183 kb)
Rights and permissions
About this article
Cite this article
de Riedmatten, H., Afzelius, M., Staudt, M. et al. A solid-state light–matter interface at the single-photon level. Nature 456, 773–777 (2008). https://doi.org/10.1038/nature07607
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature07607
This article is cited by
-
Controlling single rare earth ion emission in an electro-optical nanocavity
Nature Communications (2023)
-
Optimizing Raman quantum memory with dynamic phase
Science China Information Sciences (2023)
-
Rare-earth quantum memories: The experimental status quo
Frontiers of Physics (2023)
-
Ultra-narrow optical linewidths in rare-earth molecular crystals
Nature (2022)
-
Experimental demonstration of memory-enhanced scaling for entanglement connection of quantum repeater segments
Nature Photonics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.