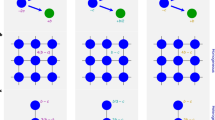
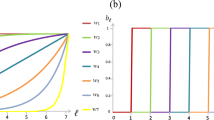
Abstract
Humans often cooperate in public goods games1,2,3 and situations ranging from family issues to global warming4,5. However, evolutionary game theory predicts4,6 that the temptation to forgo the public good mostly wins over collective cooperative action, and this is often also seen in economic experiments7. Here we show how social diversity provides an escape from this apparent paradox. Up to now, individuals have been treated as equivalent in all respects4,8, in sharp contrast with real-life situations, where diversity is ubiquitous. We introduce social diversity by means of heterogeneous graphs and show that cooperation is promoted by the diversity associated with the number and size of the public goods game in which each individual participates and with the individual contribution to each such game. When social ties follow a scale-free distribution9, cooperation is enhanced whenever all individuals are expected to contribute a fixed amount irrespective of the plethora of public goods games in which they engage. Our results may help to explain the emergence of cooperation in the absence of mechanisms based on individual reputation and punishment10,11,12. Combining social diversity with reputation and punishment will provide instrumental clues on the self-organization of social communities and their economical implications.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Hardin, G. The tragedy of the commons. Science 162, 1243–1248 (1968)
Binmore, K. G. Game Theory and the Social Contract Vol. 1, Playing Fair (MIT Press, Cambridge, MA, 1994)
Kollock, P. Social dilemmas: The anatomy of cooperation. Annu. Rev. Sociol. 24, 183–214 (1998)
Hauert, C., De Monte, S., Hofbauer, J. & Sigmund, K. Volunteering as Red Queen mechanism for cooperation in public goods games. Science 296, 1129–1132 (2002)
Milinski, M., Semmann, D., Krambeck, H. J. & Marotzke, J. Stabilizing the Earth’s climate is not a losing game: Supporting evidence from public goods experiments. Proc. Natl Acad. Sci. USA 103, 3994–3998 (2006)
Hofbauer, J. & Sigmund, K. Evolutionary Games and Population Dynamics (Cambridge Univ. Press, Cambridge, 1998)
Fehr, E. & Gachter, S. Altruistic punishment in humans. Nature 415, 137–140 (2002)
Szabo, G. & Hauert, C. Phase transitions and volunteering in spatial public goods games. Phys. Rev. Lett. 89, 118101 (2002)
Barabási, A. L. & Albert, R. Emergence of scaling in random networks. Science 286, 509–512 (1999)
Ohtsuki, H. & Iwasa, Y. How should we define goodness?—reputation dynamics in indirect reciprocity. J. Theor. Biol. 231, 107–120 (2004)
Nowak, M. A. & Sigmund, K. Evolution of indirect reciprocity. Nature 437, 1291–1298 (2005)
Pacheco, J. M., Santos, F. C. & Chalub, F. A. Stern-judging: A simple, successful norm which promotes cooperation under indirect reciprocity. PLoS Comput. Biol. 2, e178 (2006)
Hauert, C., Traulsen, A., Brandt, H., Nowak, M. A. & Sigmund, K. Via freedom to coercion: the emergence of costly punishment. Science 316, 1905–1907 (2007)
Boyd, R. & Mathew, S. Behavior. A narrow road to cooperation. Science 316, 1858–1859 (2007)
Szabo, G. & Hauert, C. Evolutionary prisoner’s dilemma games with voluntary participation. Phys. Rev. E 66, 062903 (2002)
Santos, F. C. & Pacheco, J. M. Scale-free networks provide a unifying framework for the emergence of cooperation. Phys. Rev. Lett. 95, 098104 (2005)
Santos, F. C., Pacheco, J. M. & Lenaerts, T. Evolutionary dynamics of social dilemmas in structured heterogeneous populations. Proc. Natl Acad. Sci. USA 103, 3490–3494 (2006)
Ohtsuki, H., Hauert, C., Lieberman, E. & Nowak, M. A. A simple rule for the evolution of cooperation on graphs and social networks. Nature 441, 502–505 (2006)
Amaral, L. A., Scala, A., Barthelemy, M. & Stanley, H. E. Classes of small-world networks. Proc. Natl Acad. Sci. USA 97, 11149–11152 (2000)
Albert, R. & Barabási, A. L. Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97 (2002)
Dorogotsev, S. N. & Mendes, J. F. F. Evolution of Networks: From Biological Nets to the Internet and WWW. (Oxford Univ. Press, Oxford, 2003)
Lieberman, E., Hauert, C. & Nowak, M. A. Evolutionary dynamics on graphs. Nature 433, 312–316 (2005)
Nowak, M. A. & May, R. M. Evolutionary games and spatial chaos. Nature 359, 826–829 (1992)
Nowak, M. A. Five rules for the evolution of cooperation. Science 314, 1560–1563 (2006)
Boehm, C. Hierarchy in the Forest: The Evolution of Egalitarian Behavior (Harvard Univ. Press, Cambridge, MA, 1999)
Skyrms, B. The Stag Hunt and the Evolution of Social Structure (Cambridge Univ. Press, Cambridge, 2004)
Santos, F. C. & Pacheco, J. M. A new route to the evolution of cooperation. J. Evol. Biol. 19, 726–733 (2006)
Traulsen, A., Nowak, M. A. & Pacheco, J. M. Stochastic dynamics of invasion and fixation. Phys. Rev. E 74, 011909 (2006)
Hauert, C. & Doebeli, M. Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nature 428, 643–646 (2004)
Ohtsuki, H., Nowak, M. A. & Pacheco, J. M. Breaking the symmetry between interaction and replacement in evolutionary dynamics on graphs. Phys. Rev. Lett. 98, 108106 (2007)
Acknowledgements
F.C.S. acknowledges support from Fonds de la Recherche Scientifique, Belgium. M.D.S. and J.M.P. acknowledge financial support from Fundação para a Ciência e Tecnologia, Portugal.
Author information
Authors and Affiliations
Corresponding author
Supplementary information
Supplementary information
s file contains supplementary text and Supplementary Figures S1-S8. (PDF 2465 kb)
Rights and permissions
About this article
Cite this article
Santos, F., Santos, M. & Pacheco, J. Social diversity promotes the emergence of cooperation in public goods games. Nature 454, 213–216 (2008). https://doi.org/10.1038/nature06940
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature06940
This article is cited by
-
Strategy evolution on higher-order networks
Nature Computational Science (2024)
-
On Parameterized Complexity of Binary Networked Public Goods Game
Algorithmica (2024)
-
Robust Strategy Optimization of Networked Evolutionary Games with Disturbance Inputs
Dynamic Games and Applications (2024)
-
Strategy Consensus of Networked Evolutionary Games with Time Invariant Delays
Dynamic Games and Applications (2023)
-
The evolutionary extortion game of multiple groups in hypernetworks
Scientific Reports (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.