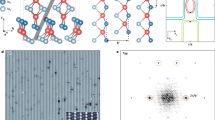
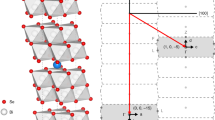
Abstract
Formation of electron pairs is essential to superconductivity. For conventional superconductors, tunnelling spectroscopy has established that pairing is mediated by bosonic modes (phonons); a peak in the second derivative of tunnel current d2I/dV2 corresponds to each phonon mode1,2,3. For high-transition-temperature (high-Tc) superconductivity, however, no boson mediating electron pairing has been identified. One explanation could be that electron pair formation4 and related electron–boson interactions are heterogeneous at the atomic scale and therefore challenging to characterize. However, with the latest advances in d2I/dV2 spectroscopy using scanning tunnelling microscopy, it has become possible to study bosonic modes directly at the atomic scale5. Here we report d2I/dV2 imaging6,7,8 studies of the high-Tc superconductor Bi2Sr2CaCu2O8+δ. We find intense disorder of electron–boson interaction energies at the nanometre scale, along with the expected modulations in d2I/dV2 (refs 9, 10). Changing the density of holes has minimal effects on both the average mode energies and the modulations, indicating that the bosonic modes are unrelated to electronic or magnetic structure. Instead, the modes appear to be local lattice vibrations, as substitution of 18O for 16O throughout the material reduces the average mode energy by approximately 6 per cent—the expected effect of this isotope substitution on lattice vibration frequencies5. Significantly, the mode energies are always spatially anticorrelated with the superconducting pairing-gap energies, suggesting an interplay between these lattice vibration modes and the superconductivity.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
McMillan, W. L. & Rowell, J. M. in Superconductivity Vol. 1 (ed. Parks, R. D.) 561 (Dekker, New York, 1969)
Scalapino, D. J. in Superconductivity Vol. 1 (ed. Parks, R. D.) 449 (Dekker, New York, 1969)
Carbotte, J. P. Properties of boson-exchange superconductors. Rev. Mod. Phys. 62, 1027–1157 (1990)
Nunner, T. S., Andersen, B. M., Melikyan, A. & Hirschfeld, P. J. Dopant-modulated pair interaction in cuprate superconductors. Phys. Rev. Lett. 95, 177003 (2005)
Stipe, B. C., Rezaei, M. A. & Ho, W. Single-molecule vibrational spectroscopy and microscopy. Science 280, 1732–1735 (1998)
Morr, D. K. & Nyberg, R. H. Localized bosonic modes in superconductors. Phys. Rev. B 68, 060505 (2003)
Han, J. H. Signature of a collective spin mode in the local tunnelling spectra of a d-wave superconductor. Phys. Rev. B 67, 094506 (2003)
Balatsky, A. V., Abanov, Ar. & Zhu, J.-X. Inelastic tunnelling spectroscopy in a d-wave superconductor. Phys. Rev. B 68, 214506 (2003)
Zhu, J.-X., Sun, J., Si, Q. & Balatsky, A. V. Effects of a collective spin resonance mode on the scanning tunnelling microscopy spectra of d-wave superconductors. Phys. Rev. Lett. 92, 017002 (2004)
Zhu, J.-X. et al. Effects of τ1 scattering on Fourier-transformed inelastic tunnelling spectra in high-Tc cuprates with bosonic modes. Preprint at http://www.arXiv.org/cond-mat/0507621 (2005).
Eliashberg, G. M. Interactions between electrons and lattice vibrations in a superconductor. Sov. Phys. JETP 11, 696–702 (1960)
McQueeney, R. J. et al. Anomalous dispersion of LO phonons in La1.85Sr0.15CuO4 at low temperatures. Phys. Rev. Lett. 82, 628–631 (1999)
Reznik, D. et al. Electron-phonon coupling reflecting dynamic charge inhomogeneity in copper oxide superconductors. Nature 440, 1170–1173 (2006)
Egami, T. Competing interactions in complex oxides: Polaron stability in manganites and cuprates. AIP Conf. Proc. 554, 38–47 (2001)
Sidis, Y. et al. Magnetic resonant excitations in high-Tc superconductors. Phys. Status Solidi B 241, 1204–1210 (2004)
Tranquada, J. M. et al. Quantum magnetic excitations from stripes in copper oxide superconductors. Nature 429, 534–538 (2004)
Hayden, S. M., Mook, H. A., Dai, P., Perring, T. G. & Doğan, F. The structure of the high-energy spin excitations in a high-transition-temperature superconductor. Nature 429, 531–534 (2004)
Bogdanov, P. V. et al. Evidence for an energy scale for quasiparticle dispersion in Bi2Sr2CaCu2O8 . Phys. Rev. Lett. 85, 2581–2584 (2000)
Kaminski, A. et al. Renormalization of spectral line shape and dispersion below Tc in Bi2Sr2CaCu2O8+δ . Phys. Rev. Lett. 86, 1070–1073 (2001)
Johnson, P. D. et al. Doping and temperature dependence of the mass enhancement observed in the cuprate Bi2Sr2CaCu2O8+δ . Phys. Rev. Lett. 87, 177007 (2001)
Lanzara, A. et al. Evidence for ubiquitous strong electron-phonon coupling in high-temperature superconductors. Nature 412, 510–514 (2001)
Norman, M. R. et al. Unusual dispersion and line shape of the superconducting state spectra of Bi2Sr2CaCu2O8+δ . Phys. Rev. Lett. 79, 3506–3509 (1997)
Borisenko, S. V. et al. Anomalous enhancement of the coupling to the magnetic resonance mode in underdoped Pb-Bi2212. Phys. Rev. Lett. 90, 207001 (2003)
Gromko, A. D. et al. Mass-renormalized electronic excitations at (π,0) in the superconducting state of Bi2Sr2CaCu2O8+δ . Phys. Rev. B 68, 174520 (2003)
Cuk, T. et al. Coupling of the B1g phonon to the antinodal electronic states of Bi2Sr2Ca0.92Y0.08Cu2O8+δ . Phys. Rev. Lett. 93, 117003 (2004)
Gweon, G.-H. et al. An unusual isotope effect in a high-transition-temperature superconductor. Nature 430, 187–190 (2004)
Miyakawa, N. et al. Predominantly superconducting origin of large energy gaps in underdoped Bi2Sr2CaCu2O8+δ from tunnelling spectroscopy. Phys. Rev. Lett. 83, 1018–1021 (1999)
Romano, P. et al. Modelling study of the dip/hump feature in Bi2Sr2CaCu2O8+δ tunnelling spectroscopy. Preprint at http://www.arXiv.org/cond-mat/0602405 (2006).
Carbotte, J. P., Schachinger, E. & Basov, D. N. Coupling strength of charge carriers to spin fluctuations in high-temperature superconductors. Nature 401, 354–356 (1999)
Hwang, J., Timusk, T. & Gu, G. D. High-transition-temperature superconductivity in the absence of the magnetic-resonance mode. Nature 427, 714–717 (2004)
Zhu, J.-X. & Balatsky, A. V. Local strong coupling pairing in d-wave superconductor with inhomogeneous bosonic modes. Preprint at http://www.arXiv.org/cond-mat/0604391 (2006).
Pilgram, S., Rice, T. M. & Sigrist, M. Role of inelastic tunneling through the barrier in scanning tunneling microscope experiments on cuprates. Preprint at http://www.arXiv.org/cond-mat/0605646 (2006).
Acknowledgements
We thank the following people for discussions and communications: Ar. Abanov, P. W. Anderson, N. Ashcroft, T. P. Devereaux, T. Egami, M. Eshrig, C. Henley, P. J. Hirschfeld, A. Lanzara, D.-H. Lee, P. Littlewood, D. Morr, K. A. Müller, M. R. Norman, J. Orenstein, T. M. Rice, J. Rowell, D. J. Scalapino, Z.-X. Shen, C. M. Varma and A. Zettl. This work was supported by an LDRD from Los Alamos National Laboratory, a Grant-in-Aid for Scientific Research from the Ministry of Science and Education (Japan), the 21st-Century COE Program of JSPS, by Cornell University and by the Office of Naval Research; K.F. acknowledges Fellowship support from the ICAM International Materials Institute.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
Reprints and permissions information is available at npg.nature.com/reprintsandpermissions. The authors declare no competing financial interests.
Supplementary information
Supplementary Figures
This file contains Supplementary Figures 1–3 (PDF 262 kb)
Rights and permissions
About this article
Cite this article
Lee, J., Fujita, K., McElroy, K. et al. Interplay of electron–lattice interactions and superconductivity in Bi2Sr2CaCu2O8+δ. Nature 442, 546–550 (2006). https://doi.org/10.1038/nature04973
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature04973
This article is cited by
-
Traces of electron-phonon coupling in one-dimensional cuprates
Nature Communications (2023)
-
Stripe correlations in the two-dimensional Hubbard-Holstein model
Communications Physics (2022)
-
Evidence for unconventional superconductivity in twisted trilayer graphene
Nature (2022)
-
Enhancement of superconductivity on the verge of a structural instability in isovalently doped β-ThRh1−xIrxGe
npj Quantum Materials (2022)
-
Direct probing of phonon mode specific electron–phonon scatterings in two-dimensional semiconductor transition metal dichalcogenides
Nature Communications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.