Abstract
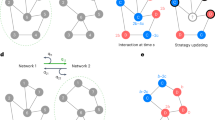
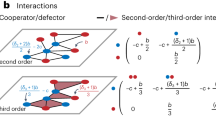
A fundamental aspect of all biological systems is cooperation. Cooperative interactions are required for many levels of biological organization ranging from single cells to groups of animals1,2,3,4. Human society is based to a large extent on mechanisms that promote cooperation5,6,7. It is well known that in unstructured populations, natural selection favours defectors over cooperators. There is much current interest, however, in studying evolutionary games in structured populations and on graphs8,9,10,11,12,13,14,15,16,17. These efforts recognize the fact that who-meets-whom is not random, but determined by spatial relationships or social networks18,19,20,21,22,23,24. Here we describe a surprisingly simple rule that is a good approximation for all graphs that we have analysed, including cycles, spatial lattices, random regular graphs, random graphs and scale-free networks25,26: natural selection favours cooperation, if the benefit of the altruistic act, b, divided by the cost, c, exceeds the average number of neighbours, k, which means b/c > k. In this case, cooperation can evolve as a consequence of ‘social viscosity’ even in the absence of reputation effects or strategic complexity.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Hamilton, W. D. The genetical evolution of social behaviour. J. Theor. Biol. 7, 1–16 (1964)
Trivers, R. The evolution of reciprocal altruism. Q. Rev. Biol. 46, 35–57 (1971)
Axelrod, R. & Hamilton, W. D. The evolution of cooperation. Science 211, 1390–1396 (1981)
Wilson, E. O. Sociobiology (Harvard Univ. Press, Cambridge, Massachusetts, 1975)
Wedekind, C. & Milinski, M. Cooperation through image scoring in humans. Science 288, 850–852 (2000)
Fehr, E. & Fischbacher, U. The nature of human altruism. Nature 425, 785–791 (2003)
Nowak, M. A. & Sigmund, K. Evolution of indirect reciprocity. Nature 437, 1291–1298 (2005)
Nowak, M. A. & May, R. M. Evolutionary games and spatial chaos. Nature 359, 826–829 (1992)
Killingback, T. & Doebeli, M. Spatial evolutionary game theory: Hawks and Doves revisited. Proc. R. Soc. Lond. B 263, 1135–1144 (1996)
Nakamaru, M., Matsuda, H. & Iwasa, Y. The evolution of cooperation in a lattice-structured population. J. Theor. Biol. 184, 65–81 (1997)
van Baalen, M. & Rand, D. A. The unit of selection in viscous populations and the evolution of altruism. J. Theor. Biol. 193, 631–648 (1998)
Mitteldorf, J. & Wilson, D. S. Population viscosity and the evolution of altruism. J. Theor. Biol. 204, 481–496 (2000)
Hauert, C., De Monte, S., Hofbauer, J. & Sigmund, K. Volunteering as red queen mechanism for cooperation in public goods games. Science 296, 1129–1132 (2002)
Le Galliard, J., Ferriere, R. & Dieckman, U. The adaptive dynamics of altruism in spatially heterogeneous populations. Evolution 57, 1–17 (2003)
Hauert, C. & Doebeli, M. Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nature 428, 643–646 (2004)
Ifti, M., Killingback, T. & Doebeli, M. Effects of neighbourhood size and connectivity on the spatial continuous prisoner's dilemma. J. Theor. Biol. 231, 97–106 (2004)
Santos, F. C. & Pacheco, J. M. Scale-free networks provide a unifying framework for the emergence of cooperation. Phys. Rev. Lett. 95, 098104 (2005)
Levin, S. A. & Paine, R. T. Disturbance, patch formation, and community structure. Proc. Natl Acad. Sci. USA 71, 2744–2747 (1974)
Durrett, R. & Levin, S. A. The importance of being discrete (and spatial). Theor. Popul. Biol. 46, 363–394 (1994)
Hassell, M. P., Comins, H. N. & May, R. M. Species coexistence and self-organizing spatial dynamics. Nature 370, 290–292 (1994)
Skyrms, B. & Pemantle, R. A dynamic model of social network formation. Proc. Natl Acad. Sci. USA 97, 9340–9346 (2000)
Abramson, G. & Kuperman, M. Social games in a social network. Phys. Rev. E 63, 030901 (2001)
Szabó, G. & Vukov, J. Cooperation for volunteering and partially random partnership. Phys. Rev. E 69, 036107 (2004)
Lieberman, E., Hauert, C. & Nowak, M. A. Evolutionary dynamics on graphs. Nature 433, 312–316 (2005)
Watts, D. J. & Strogatz, S. H. Collective dynamics of 'small-world' networks. Nature 393, 440–442 (1998)
Barabasi, A. & Albert, R. Emergence of scaling in random networks. Science 286, 509–512 (1999)
Taylor, P. D. & Jonker, L. Evolutionary stable strategies and game dynamics. Math. Biosci. 40, 145–156 (1978)
Hofbauer, J. & Sigmund, K. Evolutionary Games and Population Dynamics (Cambridge Univ. Press, Cambridge, UK, 1998)
Nowak, M. A., Sasaki, A., Taylor, C. & Fudenberg, D. Emergence of cooperation and evolutionary stability in finite populations. Nature 428, 646–650 (2004)
Wild, G. & Taylor, P. D. Fitness and evolutionary stability in game theoretic models of finite populations. Proc. R. Soc. Lond. B 271, 2345–2349 (2004)
Acknowledgements
Support from the John Templeton Foundation, JSPS, NDSEG and Harvard-MIT HST is gratefully acknowledged. The Program for Evolutionary Dynamics at Harvard University is sponsored by Jeffrey Epstein.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
Reprints and permissions information is available at npg.nature.com/reprintsandpermissions. The authors declare no competing financial interests.
Supplementary information
Supplementary Notes
This file contains the Supplementary Discussion, Supplementary Figure 4 and additional references. (PDF 248 kb)
Rights and permissions
About this article
Cite this article
Ohtsuki, H., Hauert, C., Lieberman, E. et al. A simple rule for the evolution of cooperation on graphs and social networks. Nature 441, 502–505 (2006). https://doi.org/10.1038/nature04605
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature04605
This article is cited by
-
The collapse of cooperation during range expansion of Pseudomonas aeruginosa
Nature Microbiology (2024)
-
Humans strategically avoid connecting to others who agree and avert the emergence of network polarization in a coordination task
Scientific Reports (2023)
-
Strategy evolution on dynamic networks
Nature Computational Science (2023)
-
Flipping the intuition for games on dynamic networks
Nature Computational Science (2023)
-
Evolution of cooperation in multiplex networks through asymmetry between interaction and replacement
Scientific Reports (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.