Abstract
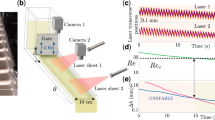
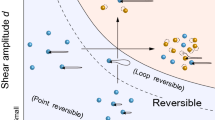
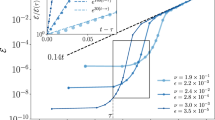
Systems governed by time reversible equations of motion often give rise to irreversible behaviour1,2,3. The transition from reversible to irreversible behaviour is fundamental to statistical physics, but has not been observed experimentally in many-body systems. The flow of a newtonian fluid at low Reynolds number can be reversible: for example, if the fluid between concentric cylinders is sheared by boundary motion that is subsequently reversed, then all fluid elements return to their starting positions4. Similarly, slowly sheared suspensions of solid particles, which occur widely in nature and science5, are governed by time reversible equations of motion. Here we report an experiment showing precisely how time reversibility6 fails for slowly sheared suspensions. We find that there is a concentration dependent threshold for the deformation or strain beyond which particles do not return to their starting configurations after one or more cycles. Instead, their displacements follow the statistics of an anisotropic random walk7. By comparing the experimental results with numerical simulations, we demonstrate that the threshold strain is associated with a pronounced growth in the Lyapunov exponent (a measure of the strength of chaotic particle interactions). The comparison illuminates the connections between chaos, reversibility and predictability.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Tolman, R. C. The Principles of Statistical Mechanics (Oxford Univ. Press, London, 1938)
Boffeta, G., Cencini, M., Falcioni, M. & Vulpiani, A. Predictability: a way to characterize complexity. Phys. Rep. 356, 367–474 (2002)
Wang, G. M., Sevick, E. M., Mittag, E., Searles, D. J. & Evans, D. J. Experimental demonstration of violations of the second law of thermodynamics for small systems and short time scales. Phys. Rev. Lett. 89, 050601 (2002)
Leal, L. G. Laminar Flow and Convective Transport Processes: Scaling Principles and Asymptotic Analysis (Butterworth-Heinemann, Boston, 1992)
Morrison, I. D. & Ross, S. Colloidal Dispersions: Suspensions, Emulsions, and Foams (Wiley-Interscience, Hoboken, 2003)
Lamb, J. S. W. & Roberts, J. A. G. Time-reversal symmetry in dynamical systems: a survey. Physica D 112, 1–39 (1998)
Berg, H. C. Random Walks in Biology (Princeton Univ. Press, Princeton, New Jersey, 1993)
Taylor, G. I. & Friedman, J. Low Reynolds Number Flows (National Committee on Fluid Mechanics Films, Encyclopedia Britannica Educational Corp., United States, 1966); available as ‘G. I. Taylor and Kinematic Reversibility’ in Multi-Media Fluid Mechanics CD-ROM (eds Homsy, G. M.) (Cambridge Univ. Press, Cambridge, 2000).
Aref, H. Chaotic advection of fluid particles. Phil. Trans. R. Soc. Lond. A 333, 273–288 (1990)
Drazer, D., Koplik, J., Khusid, B. & Acrivos, A. Deterministic and stochastic behaviour of non-Brownian spheres in sheared suspensions. J. Fluid Mech. 460, 307–335 (2002)
Jánosi, I. M., Tél, T., Wolf, D. E. & Gallas, J. A. C. Chaotic particle dynamics in viscous flows: The three-particle Stokeslet problem. Phys. Rev. E 56, 2858–2866 (1997)
Lighthill, J. The recently recognized failure of predictability in Newtonian dynamics. Proc. R. Soc. Lond. A 407, 35–48 (1986)
Eckstein, E. C., Bailey, D. G. & Shapiro, A. H. Self-diffusion of particles in shear-flow of a suspension. J. Fluid Mech. 79, 191–208 (1977)
Leighton, D. & Acrivos, A. Measurement of shear-induced migration of particles in concentrated suspensions. J. Fluid Mech. 177, 109–131 (1987)
Breedveld, V., van den Ende, D., Tripathi, A. & Acrivos, A. The measurement of the shear-induced particle and fluid tracer diffusivities by a novel method. J. Fluid Mech. 375, 297–318 (1998)
Breedveld, V., van den Ende, D. & Jongschaap, R. Shear-induced diffusion and rheology of noncolloidal suspensions: Time scales and particle displacements. J. Chem. Phys. 114, 5923–5936 (2001)
Zarraga, I. E. & Leighton, D. T. Measurement of an unexpectedly large shear-induced self-diffusivity in a dilute suspension of spheres. Phys. Fluids 14, 2194–2201 (2002)
Marchioro, M. & Acrivos, A. Shear-induced particle diffusivities from numerical simulations. J. Fluid Mech. 443, 101–128 (2001)
Sierou, A. & Brady, J. F. Shear-induced self-diffusion in non-colloidal suspensions. J. Fluid Mech. 506, 285–314 (2004)
Segrè, P. N., Herbolzheimer, E. & Chaikin, P. M. Long-range correlations in sedimentation. Phys. Rev. Lett. 79, 2574–2577 (1997)
Segrè, P. N., Liu, F., Umbanhowar, P. & Weitz, D. A. An effective gravitational temperature for sedimentation. Nature 409, 594–597 (2001)
Voth, G. A. et al. Ordered clusters and dynamical states of particles in a vibrated fluid. Phys. Rev. Lett. 88, 234301 (2002)
Krishnan, G. P., Beimfohr, S. & Leighton, D. T. Shear-induced radial segregation in bidisperse suspensions. J. Fluid Mech. 321, 371–393 (1996)
Crocker, J. C. & Grier, D. G. Methods of digital video microscopy for colloidal studies. J. Colloid Interf. Sci. 179, 298–310 (1996)
Taylor, G. I. Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219, 186–203 (1953)
Sussman, G. J. & Wisdom, J. Chaotic evolution of the solar system. Science 257, 56–62 (1992)
Acknowledgements
We appreciate discussions with L. G. Leal and G. Homsy. K. Knipmeyer and E. Knowlton provided assistance with data acquisition and reduction. This work was supported by the Keck Foundation (D.J.P.), the National Science Foundation (J.P.G.) and the US-Israel Binational Science Foundation (A.M.L.). The work was initiated during a granular physics workshop hosted by the Kavli Institute for Theoretical Physics at UCSB. Author Contributions D.J.P and J.P.G. were responsible for the experiments; J.F.B. and A.M.L. did the numerical simulations.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
Reprints and permissions information is available at npg.nature.com/reprintsandpermissions. The authors declare no competing financial interests.
Supplementary information
Supplementary Video 1
This is a continuously sampled movie clip showing the motion of tracer particles in an oscillatory shear flow. (MOV 3413 kb)
Supplementary Video 2
This movie is a periodically sampled clip showing the reversible motion of tracer particles in an oscillatory shear flow. The shear strain amplitude is 1.0, which is just below the irreversibility threshold. (MOV 5151 kb)
Supplementary Video 3
This movie is a periodically sampled clip showing the irreversible motion of tracer particles in an oscillatory shear flow with a shear strain amplitude of 2.5, which is above the irreversibility threshold. (MOV 4751 kb)
Supplementary Video Legends
This provides information about the experimental conditions under which Supplementary Videos 1, 2, and 3 were obtained. (PDF 26 kb)
Rights and permissions
About this article
Cite this article
Pine, D., Gollub, J., Brady, J. et al. Chaos and threshold for irreversibility in sheared suspensions. Nature 438, 997–1000 (2005). https://doi.org/10.1038/nature04380
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature04380
This article is cited by
-
Critical behavior of nonequilibrium depinning transitions for vortices driven by current and vortex density
Scientific Reports (2022)
-
Model architecture can transform catastrophic forgetting into positive transfer
Scientific Reports (2022)
-
Critical behavior of density-driven and shear-driven reversible–irreversible transitions in cyclically sheared vortices
Scientific Reports (2021)
-
The microstructural change causing the failure of the Cox-Merz rule in Newtonian suspensions: experiments and simulations
Rheologica Acta (2021)
-
Insights into the Payne Effect of Carbon Black Filled Styrene-butadiene Rubber Compounds
Chinese Journal of Polymer Science (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.