Abstract
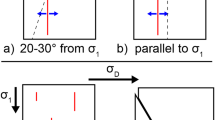
Faults in brittle rock are shear fractures formed through the interaction and coalescence of many tensile microcracks1,2,3. The geometry of these microcracks and their surrounding elastic stress fields control the orientation of the final shear fracture surfaces3,4. The classic Coulomb–Mohr failure criterion5 predicts the development of two conjugate (bimodal) shear planes that are inclined at an acute angle to the axis of maximum compressive stress. This criterion, however, is incapable of explaining the three-dimensional polymodal fault patterns that are widely observed in rocks6,7,8,9. Here we show that the elastic stress around tensile microcracks in three dimensions promotes a mutual interaction that produces brittle shear planes oriented obliquely to the remote principal stresses, and can therefore account for observed polymodal fault patterns. Our microcrack interaction model is based on the three-dimensional solution of Eshelby10,11, unlike previous models4,12 that employed two-dimensional approximations. Our model predicts that shear fractures formed by the coalescence of interacting mode I cracks will be inclined at a maximum of 26° to the axes of remote maximum and intermediate compression. An improved understanding of brittle shear failure in three dimensions has important implications for earthquake seismology and rock-mass stability, as well as fluid migration in fractured rocks13.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Paterson, M. S. Experimental Rock Deformation—The Brittle Field Ch. 3 & 4 (Springer, Berlin, 1978)
Lockner, D. A., Byerlee, J. D., Kuksenko, V., Ponomarev, A. & Sidorin, A. Observations of quasistatic fault growth from acoustic emissions. in Fault Mechanics and Transport Properties of Rocks (eds Evans, B. & Wong, T.) 3–31 (Academic, London, 1992)
Scholz, C. H. The Mechanics of Earthquakes and Faulting Ch. 1 & 3 (Cambridge Univ. Press, Cambridge, UK, 2002)
Reches, Z. & Lockner, D. A. Nucleation and growth of faults in brittle rocks. J. Geophys. Res. 99, 18159–18173 (1994)
Jaeger, J. & Cook, N. G. W. Fundamentals of Rock Mechanics, 3rd edn, Ch. 4 & 6 (Chapman & Hall, London, 1979)
Reches, Z. Analysis of faulting in three-dimensional strain fields. Tectonophysics 47, 109–129 (1978)
Aydin, A. & Reches, Z. Number and orientation of fault sets in the field and in experiments. Geology 10, 107–112 (1982)
Reches, Z. Faulting of rocks in three-dimensional strain fields. II. Theoretical analysis. Tectonophysics 95, 133–156 (1983)
Reches, Z. & Dieterich, J. Faulting of rocks in three-dimensional strain fields. I. Failure of rocks in polyaxial, servo-control experiments. Tectonophysics 95, 111–132 (1983)
Eshelby, J. D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. A 241, 376–396 (1957)
Eshelby, J. D. The elastic field outside an ellipsoidal inclusion. Proc. R. Soc. Lond. A 252, 561–569 (1959)
Du, Y. & Aydin, A. Interaction of multiple cracks and formation of echelon crack arrays. Int. J. Num. Analyt. Methods Geomech. 15, 205–218 (1991)
Sternlof, K. R., Chapin, J. R., Pollard, D. D. & Durlofsky, L. J. Permeability effects of deformation band arrays in sandstone. AAPG Bull. 88, 1315–1329 (2004)
Anderson, E. M. The Dynamics Of Faulting And Dyke Formation With Applications To Britain (Oliver and Boyd, Edinburgh, 1942)
De Paola, N., Holdsworth, R. E. & McCaffrey, K. J. W. The influence of lithology and pre-existing structures on reservoir-scale faulting patterns in transtensional rift zones. J. Geol. Soc. Lond. 162, 471–480 (2005)
Crider, J. G. Oblique slip and the geometry of normal-fault linkage: mechanics and a case study from the Basin and Range in Oregon. J. Struct. Geol. 23, 1997–2009 (2001)
Beacom, L. E., Anderson, T. B. & Holdsworth, R. E. Using basement-hosted clastic dykes as syn-rifting palaeostress indicators: an example from the basal Stoer group, northwest Scotland. Geol. Mag. 136, 301–310 (1999)
Dewey, J. F., Holdsworth, R. E. & Strachan, R. A. in Continental Transpressional and Transtensional Tectonics (eds Holdsworth, R. E., Strachan, R. A. & Dewey, J. F.) Vol. 135 1–14 (Geological Society Special Publications, London, 1998)
Jones, R. R., Holdsworth, R. E., McCaffrey, K. J. W., Clegg, P. & Tavarnelli, E. Scale dependence, strain compatibility and heterogeneity of three-dimensional deformation during mountain building: a discussion. J. Struct. Geol. 27, 1190–1204 (2005)
Moore, D. E. & Lockner, D. A. The role of microcracking in shear-fracture propagation in granite. J. Struct. Geol. 17, 95–114 (1995)
Glover, P. W. J., Gomez, J. B. & Meredith, P. G. Fracturing in saturated rocks undergoing triaxial deformation using complex electrical conductivity measurements: experimental study. Earth Planet. Sci. Lett. 183, 201–213 (2000)
Ju, J. W. & Sun, L. Z. Effective elastoplastic behaviour of metal matrix composites containing randomly located aligned spheroidal inhomogeneities. Part 1: micromechanics based formulation. Int. J. Solids Struct. 38, 183–201 (2001)
Peng, S. & Johnson, A. M. Crack growth and faulting in cylindrical specimens of Chelmsford granite. Int. J. Rock Mech. Mining Sci. 9, 37–86 (1972)
Pollard, D. D. & Segall, P. Theoretical displacements and stresses near fractures in rock: with applications to faults, joints, veins, dikes, and solution surfaces. in Fracture Mechanics of Rock (ed. Atkinson, B. K) 277–349 (Academic, London, 1987)
McCaffrey, K. J. W. et al. Unlocking the spatial dimension: digital technologies and the future of geoscience fieldwork. J. Geol. Soc. Lond. 162, 927–938 (2005)
Morris, A., Ferrill, D. A. & Henderson, D. B. Slip-tendency analysis and fault reactivation. Geology 24, 275–278 (1996)
Petit, J.-P. & Barquins, M. Can natural faults propagate under mode II conditions? Tectonics 7, 1243–1256 (1988)
Cox, S. J. D. & Scholz, C. H. On the formation and growth of faults: an experimental study. J. Struct. Geol. 10, 413–430 (1988)
Acknowledgements
We thank L. Sun for help with benchmarking the external field solution of Eshelby, and Z. Reches for constructive reviews. Thanks also to N. Kusznir for help with conference funds and P. Meredith, N. de Paola and D. Faulkner for discussions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
Reprints and permissions information is available at npg.nature.com/reprintsandpermissions. The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Healy, D., Jones, R. & Holdsworth, R. Three-dimensional brittle shear fracturing by tensile crack interaction. Nature 439, 64–67 (2006). https://doi.org/10.1038/nature04346
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature04346
This article is cited by
-
Assessing Stress Variability in Fractured Rock Masses with Frictional Properties and Power Law Fracture Size Distributions
Rock Mechanics and Rock Engineering (2023)
-
Physical property characterization of the Waipapa greywacke: an important geothermal reservoir basement rock in New Zealand
Geothermal Energy (2022)
-
Shear characteristics and shear strength model of rock mass structural planes
Scientific Reports (2022)
-
Progressive Transition from Extension Fracture to Shear Fracture of Altered Granite During Uniaxial Tensile Tests
Rock Mechanics and Rock Engineering (2022)
-
An Analytical Microcrack-Based Rock Model with Implications for Earthquake Mechanisms Induced by Stress Changes
Mathematical Geosciences (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.