Abstract
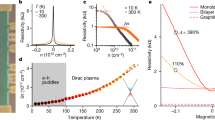
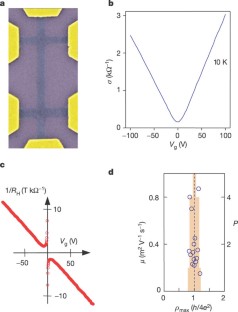
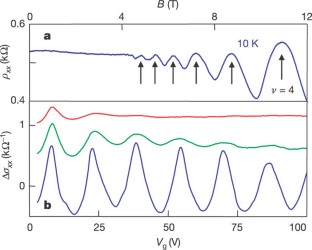
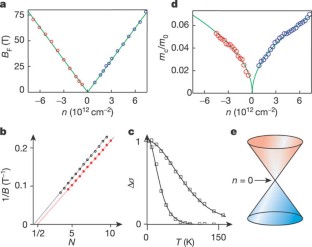
Quantum electrodynamics (resulting from the merger of quantum mechanics and relativity theory) has provided a clear understanding of phenomena ranging from particle physics to cosmology and from astrophysics to quantum chemistry1,2,3. The ideas underlying quantum electrodynamics also influence the theory of condensed matter4,5, but quantum relativistic effects are usually minute in the known experimental systems that can be described accurately by the non-relativistic Schrödinger equation. Here we report an experimental study of a condensed-matter system (graphene, a single atomic layer of carbon6,7) in which electron transport is essentially governed by Dirac's (relativistic) equation. The charge carriers in graphene mimic relativistic particles with zero rest mass and have an effective ‘speed of light’ c* ≈ 106 m s-1. Our study reveals a variety of unusual phenomena that are characteristic of two-dimensional Dirac fermions. In particular we have observed the following: first, graphene's conductivity never falls below a minimum value corresponding to the quantum unit of conductance, even when concentrations of charge carriers tend to zero; second, the integer quantum Hall effect in graphene is anomalous in that it occurs at half-integer filling factors; and third, the cyclotron mass mc of massless carriers in graphene is described by E = mcc*2. This two-dimensional system is not only interesting in itself but also allows access to the subtle and rich physics of quantum electrodynamics in a bench-top experiment.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout

Similar content being viewed by others
References
Rose, M. E. Relativistic Electron Theory (Wiley, New York, 1961)
Berestetskii, V. B., Lifshitz, E. M. & Pitaevskii, L. P. Relativistic Quantum Theory (Pergamon, Oxford, 1971)
Lai, D. Matter in strong magnetic fields. Rev. Mod. Phys. 73, 629–662 (2001)
Fradkin, E. Field Theories of Condensed Matter Systems (Westview, Oxford, 1997)
Volovik, G. E. The Universe in a Helium Droplet (Clarendon, Oxford, 2003)
Novoselov, K. S. et al. Two dimensional atomic crystals. Proc. Natl Acad. Sci. USA 102, 10451–10453 (2005)
Novoselov, K. S. et al. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004)
Zhang, Y., Small, J. P., Amori, M. E. S. & Kim, P. Electric field modulation of galvanomagnetic properties of mesoscopic graphite. Phys. Rev. Lett. 94, 176803 (2005)
Berger, C. et al. Ultrathin epitaxial graphite: 2D electron gas properties and a route toward graphene-based nanoelectronics. J. Phys. Chem. B 108, 19912–19916 (2004)
Bunch, J. S., Yaish, Y., Brink, M., Bolotin, K. & McEuen, P. L. Coulomb oscillations and Hall effect in quasi-2D graphite quantum dots. Nano Lett. 5, 287–290 (2005)
Dresselhaus, M. S. & Dresselhaus, G. Intercalation compounds of graphite. Adv. In Phys. 51, 1–186 (2002)
Brandt, N. B., Chudinov, S. M. & Ponomarev, Y. G. Semimetals 1: Graphite and Its Compounds (North-Holland, Amsterdam, 1988)
Vonsovsky, S. V. & Katsnelson, M. I. Quantum Solid State Physics (Springer, New York, 1989)
Gusynin, V. P. & Sharapov, S. G. Magnetic oscillations in planar systems with the Dirac-like spectrum of quasiparticle excitations. Phys. Rev. B 71, 125124 (2005)
Gusynin, V. P. & Sharapov, S. G. Unconventional integer quantum Hall effect in grapheme. Preprint at http://xxx.lanl.gov/abs/cond-mat/0506575 (2005).
Peres, N. M. R., Guinea, F. & Castro Neto, A. H. Electronic properties of two-dimensional carbon. Preprint at http://xxx.lanl.gov/abs/cond-mat/0506709 (2005).
Zheng, Y. & Ando, T. Hall conductivity of a two-dimensional graphite system. Phys. Rev. B 65, 245420 (2002)
Kaku, M. Introduction to Superstrings (Springer, New York, 1988)
Nakahara, M. Geometry, Topology and Physics (IOP, Bristol, 1990)
Mikitik, G. P. & Sharlai, Yu. V. Manifestation of Berry's phase in metal physics. Phys. Rev. Lett. 82, 2147–2150 (1999)
Luk'yanchuk, I. A. & Kopelevich, Y. Phase analysis of quantum oscillations in graphite. Phys. Rev. Lett. 93, 166402 (2004)
Abrahams, E., Anderson, P. W., Licciardello, D. C. & Ramakrishnan, T. V. Scaling theory of localization: Absence of quantum diffusion in two dimensions. Phys. Rev. Lett. 42, 673–676 (1979)
Fradkin, E. Critical behaviour of disordered degenerate semiconductors. Phys. Rev. B 33, 3263–3268 (1986)
Lee, P. A. Localized states in a d-wave superconductor. Phys. Rev. Lett. 71, 1887–1890 (1993)
Ziegler, K. Delocalization of 2D Dirac fermions: The role of a broken symmetry. Phys. Rev. Lett. 80, 3113–3116 (1998)
Mott, N. F. & Davis, E. A. Electron Processes in Non-Crystalline Materials (Clarendon, Oxford, 1979)
Morita, Y. & Hatsugai, Y. Near critical states of random Dirac fermions. Phys. Rev. Lett. 79, 3728–3731 (1997)
Nersesyan, A. A., Tsvelik, A. M. & Wenger, F. Disorder effects in two-dimensional d-wave superconductors. Phys. Rev. Lett. 72, 2628–2631 (1997)
Acknowledgements
We thank L. Glazman, V. Falko, S. Sharapov and A. Castro Neto for discussions. K.S.N. was supported by Leverhulme Trust. S.V.M., S.V.D. and A.A.F. acknowledge support from the Russian Academy of Science and INTAS. This research was funded by the EPSRC (UK).
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
Reprints and permissions information is available at npg.nature.com/reprintsandpermissions. The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Novoselov, K., Geim, A., Morozov, S. et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197–200 (2005). https://doi.org/10.1038/nature04233
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature04233
This article is cited by
-
Twenty years of 2D materials
Nature Physics (2024)
-
Prediction of BiS2-type pnictogen dichalcogenide monolayers for optoelectronics
npj 2D Materials and Applications (2024)
-
Quantum transport of massless Dirac fermions through wormhole-shaped curved graphene in presence of constant axial magnetic flux
Scientific Reports (2024)
-
Three-dimensional flat Landau levels in an inhomogeneous acoustic crystal
Nature Communications (2024)
-
Stepwise reduction of graphene oxide and studies on defect-controlled physical properties
Scientific Reports (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.