Abstract
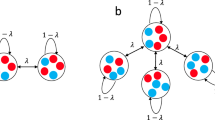
Evolutionary dynamics have been traditionally studied in the context of homogeneous or spatially extended populations1,2,3,4. Here we generalize population structure by arranging individuals on a graph. Each vertex represents an individual. The weighted edges denote reproductive rates which govern how often individuals place offspring into adjacent vertices. The homogeneous population, described by the Moran process3, is the special case of a fully connected graph with evenly weighted edges. Spatial structures are described by graphs where vertices are connected with their nearest neighbours. We also explore evolution on random and scale-free networks5,6,7. We determine the fixation probability of mutants, and characterize those graphs for which fixation behaviour is identical to that of a homogeneous population7. Furthermore, some graphs act as suppressors and others as amplifiers of selection. It is even possible to find graphs that guarantee the fixation of any advantageous mutant. We also study frequency-dependent selection and show that the outcome of evolutionary games can depend entirely on the structure of the underlying graph. Evolutionary graph theory has many fascinating applications ranging from ecology to multi-cellular organization and economics.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Liggett, T. M. Stochastic Interacting Systems: Contact, Voter and Exclusion Processes (Springer, Berlin, 1999)
Durrett, R. & Levin, S. A. The importance of being discrete (and spatial). Theor. Popul. Biol. 46, 363–394 (1994)
Moran, P. A. P. Random processes in genetics. Proc. Camb. Phil. Soc. 54, 60–71 (1958)
Durrett, R. A. Lecture Notes on Particle Systems & Percolation (Wadsworth & Brooks/Cole Advanced Books & Software, Pacific Grove, 1988)
Erdös, P. & Renyi, A. On the evolution of random graphs. Publ. Math. Inst. Hungarian Acad. Sci. 5, 17–61 (1960)
Barabasi, A. & Albert, R. Emergence of scaling in random networks. Science 286, 509–512 (1999)
Nagylaki, T. & Lucier, B. Numerical analysis of random drift in a cline. Genetics 94, 497–517 (1980)
Wright, S. Evolution in Mendelian populations. Genetics 16, 97–159 (1931)
Wright, S. The roles of mutation, inbreeding, crossbreeding and selection in evolution. Proc. 6th Int. Congr. Genet. 1, 356–366 (1932)
Fisher, R. A. & Ford, E. B. The “Sewall Wright Effect”. Heredity 4, 117–119 (1950)
Barton, N. The probability of fixation of a favoured allele in a subdivided population. Genet. Res. 62, 149–158 (1993)
Whitlock, M. Fixation probability and time in subdivided populations. Genetics 164, 767–779 (2003)
Nowak, M. A. & May, R. M. The spatial dilemmas of evolution. Int. J. Bifurcation Chaos 3, 35–78 (1993)
Hauert, C. & Doebeli, M. Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nature 428, 643–646 (2004)
Hofbauer, J. & Sigmund, K. Evolutionary Games and Population Dynamics (Cambridge Univ. Press, Cambridge, 1998)
Maruyama, T. Effective number of alleles in a subdivided population. Theor. Popul. Biol. 1, 273–306 (1970)
Slatkin, M. Fixation probabilities and fixation times in a subdivided population. Evolution 35, 477–488 (1981)
Ebel, H. & Bornholdt, S. Coevolutionary games on networks. Phys. Rev. E. 66, 056118 (2002)
Abramson, G. & Kuperman, M. Social games in a social network. Phys. Rev. E. 63, 030901(R) (2001)
Tilman, D. & Karieva, P. (eds) Spatial Ecology: The Role of Space in Population Dynamics and Interspecific Interactions (Monographs in Population Biology, Princeton Univ. Press, Princeton, 1997)
Neuhauser, C. Mathematical challenges in spatial ecology. Not. AMS 48, 1304–1314 (2001)
Pulliam, H. R. Sources, sinks, and population regulation. Am. Nat. 132, 652–661 (1988)
Hassell, M. P., Comins, H. N. & May, R. M. Species coexistence and self-organizing spatial dynamics. Nature 370, 290–292 (1994)
Reya, T., Morrison, S. J., Clarke, M. & Weissman, I. L. Stem cells, cancer, and cancer stem cells. Nature 414, 105–111 (2001)
Skyrms, B. & Pemantle, R. A dynamic model of social network formation. Proc. Nat. Acad. Sci. USA 97, 9340–9346 (2000)
Jackson, M. O. & Watts, A. On the formation of interaction networks in social coordination games. Games Econ. Behav. 41, 265–291 (2002)
Asavathiratham, C., Roy, S., Lesieutre, B. & Verghese, G. The influence model. IEEE Control Syst. Mag. 21, 52–64 (2001)
Newman, M. E. J. The structure of scientific collaboration networks. Proc. Natl Acad. Sci. USA 98, 404–409 (2001)
Boyd, S., Diaconis, P. & Xiao, L. Fastest mixing Markov chain on a graph. SIAM Rev. 46, 667–689 (2004)
Nakamaru, M., Matsuda, H. & Iwasa, Y. The evolution of cooperation in a lattice-structured population. J. Theor. Biol. 184, 65–81 (1997)
Bala, V. & Goyal, S. A noncooperative model of network formation. Econometrica 68, 1181–1229 (2000)
Acknowledgements
The Program for Evolutionary Dynamics is sponsored by J. Epstein. E.L. is supported by a National Defense Science and Engineering Graduate Fellowship. C.H. is grateful to the Swiss National Science Foundation. We are indebted to M. Brenner for many discussions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing financial interests.
Supplementary information
Supplementary Notes
These Supplementary Notes outline the derivations of the major results stated in the main text and provide a discussion of their robustness. It contains a sketch of the derivations of equation (1) for circulations and equation (2) for superstars, and also gives a brief discussion of complexity results for frequency-dependent selection and the computation underlying results for directed cycles. This closes with a discussion of assumptions about mutation rate and the interpretations of fitness that these results can accommodate. (PDF 118 kb)
Rights and permissions
About this article
Cite this article
Lieberman, E., Hauert, C. & Nowak, M. Evolutionary dynamics on graphs. Nature 433, 312–316 (2005). https://doi.org/10.1038/nature03204
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature03204
This article is cited by
-
The collapse of cooperation during range expansion of Pseudomonas aeruginosa
Nature Microbiology (2024)
-
Asymptotic behavior of mean fixation times in the Moran process with frequency-independent fitnesses
Journal of Mathematical Biology (2024)
-
Evolutionary game dynamics of multi-agent systems using local information considering hide right
Complex & Intelligent Systems (2024)
-
Mutant fixation in the presence of a natural enemy
Nature Communications (2023)
-
Prisoner’s dilemma game model Based on historical strategy information
Scientific Reports (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.