Abstract
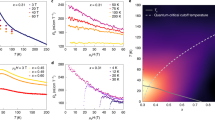
A quantum critical point (QCP) develops in a material at absolute zero when a new form of order smoothly emerges in its ground state. QCPs are of great current interest because of their singular ability to influence the finite temperature properties of materials. Recently, heavy-fermion metals have played a key role in the study of antiferromagnetic QCPs. To accommodate the heavy electrons, the Fermi surface of the heavy-fermion paramagnet is larger than that of an antiferromagnet1,2,3. An important unsolved question is whether the Fermi surface transformation at the QCP develops gradually, as expected if the magnetism is of spin-density-wave (SDW) type4,5, or suddenly, as expected if the heavy electrons are abruptly localized by magnetism6,7,8. Here we report measurements of the low-temperature Hall coefficient (RH)—a measure of the Fermi surface volume—in the heavy-fermion metal YbRh2Si2 upon field-tuning it from an antiferromagnetic to a paramagnetic state. RH undergoes an increasingly rapid change near the QCP as the temperature is lowered, extrapolating to a sudden jump in the zero temperature limit. We interpret these results in terms of a collapse of the large Fermi surface and of the heavy-fermion state itself precisely at the QCP.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Martin, R. M. Fermi-surface sum rule and its consequences for periodic Kondo and mixed-valence systems. Phys. Rev. Lett. 48, 362–365 (1982)
Fulde, P. in Narrow-Band Phenomena—Influence of Electrons with both Band and Localized Character (ed. Fuggle, J. C.) 27–29 (Plenum, New York, 1988)
Oshikawa, M. Topological approach to Luttinger's theorem and Fermi surface of a Kondo lattice. Phys. Rev. Lett. 84, 3370–3373 (2000)
Hertz, J. A. Quantum critical phenomena. Phys. Rev. B 14, 1165–1184 (1976)
Millis, A. J. Effect of a nonzero temperature on quantum critical points in itinerant fermion systems. Phys. Rev. B 48, 7183–7196 (1993)
Schröder, A. et al. Onset of antiferromagnetism in heavy-fermion metals. Nature 407, 351–355 (2000)
Coleman, P., Pépin, C., Si, Q. & Ramazashvili, R. How do Fermi liquids get heavy and die? J. Phys. Condens. Matter 13, R723–R738 (2001)
Si, Q., Rabello, S., Ingersent, K. & Smith, J. L. Locally critical quantum phase transitions in strongly correlated metals. Nature 413, 804–808 (2001)
Trovarelli, O. et al. YbRh2Si2: Pronounced non-Fermi-liquid effects above a low-lying magnetic phase transition. Phys. Rev. Lett 85, 626–629 (2000)
Ishida, K. et al. YbRh2Si2: Spin fluctuations in the vicinity of a quantum critical point at low magnetic fields. Phys. Rev. Lett. 89, 107202 (2002)
Ishida, K. et al. Low-temperature magnetic order and spin dynamics in YbRh2Si2 . Phys. Rev. B 68, 184401 (2003)
Gegenwart, P. et al. Magnetic-field induced quantum critical point in YbRh2Si2 . Phys. Rev. Lett. 89, 056402 (2002)
Küchler, R. et al. Low-temperature thermal expansion and magnetostriction of YbRh2(Si1-xGex)2 (x = 0 and 0.05). J. Magn. Magn. Mater. 272–276, 229–230 (2004)
Custers, J. et al. The break-up of heavy electrons at a quantum critical point. Nature 424, 524–527 (2003)
Stewart, G. R. Non-Fermi-liquid behavior in d- and f-electron metals. Rev. Mod. Phys. 73, 797–855 (2001)
Senthil, T., Vojta, M. & Sachdev, S. Weak magnetism and non-Fermi liquids near heavy-fermion critical points. Phys. Rev. B 69, 035111 (2004)
Paschen, S. et al. Hall effect of the NFL compound YbRh2Si2 . Acta Phys. Polon. B 34, 359–362 (2003)
Paschen, S. et al. Anomalous Hall effect in YbRh2Si2 . Physica B (in the press)
Anderson, P. W. Hall effect in the two-dimensional Luttinger liquid. Phys. Rev. Lett. 67, 2092–2094 (1991)
Nakajima, Y. et al. Normal-state Hall angle and magnetoresistance in quasi-2D heavy fermion CeCoIn5 near a quantum critical point. J. Phys. Soc. Jpn 73, 5–8 (2004)
Custers, J. Quantum-Critical Behavior in the Heavy-Fermion Compounds YbRh2Si2 and CeIn3-xSnx. PhD thesis, TU Dresden (2004)
Lee, M., Husmann, A., Rosenbaum, T. F. & Aeppli, G. High resolution study of magnetic ordering at absolute zero. Phys. Rev. Lett. 92, 187201 (2004)
Haldane, F. D. M. ‘Luttinger liquid theory’ of one-dimensional quantum fluids: I. Properties of the Luttinger model and their extension to the general 1D interacting spinless Fermi gas. J. Phys. C 14, 2585–2609 (1981)
Varma, C. M., Littlewood, P. B., Schmitt-Rink, S., Abrahams, E. & Ruckenstein, A. E. Phenomenology of the normal state of Cu-O high-temperature superconductors. Phys. Rev. Lett. 63, 1996–1999 (1989)
Valla, T. et al. Evidence for quantum critical behaviour in the optimally doped cuprate Bi2Sr2CaCu2O8+δ . Science 285, 2110–2113 (1999)
Yeh, A. et al. Quantum phase transition in a common metal. Nature 419, 459–462 (2002)
Balakirev, F. F. et al. Signature of optimal doping in Hall-effect measurements on a high-temperature superconductor. Nature 424, 912–915 (2003)
Fert, A. & Levy, P. M. Theory of the Hall effect in heavy-fermion compounds. Phys. Rev. B 36, 1907–1916 (1987)
Kontani, H., Miyazawa, M. & Yamada, K. Theory of anomalous Hall effect in a heavy fermion system with a strong anisotropic crystal field. J. Phys. Soc. Jpn 66, 2252–2255 (1997)
Norman, M. R., Si, Q., Bazaliy, Y. B. & Ramazashvili, R. Hall effect in nested antiferromagnets near the quantum critical point. Phys. Rev. Lett. 90, 116601 (2003)
Acknowledgements
We acknowledge discussions with P. Bühler, J. Custers, C. Langhammer, C. Pépin, A. Rosch, A. Schofield, M. Vojta, A. Tsvelik and F. Weickert. Part of the work at Dresden was supported by the Fonds der Chemischen Industrie. P.C. and Q.S. are supported by the National Science Foundation. The work at Rice University was partially supported by the Welch Foundation and TCSAM.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing financial interests.
Supplementary information
Supplementary Methods 1
Proof that the longitudinal field B2 produces essentially no Hall response. (PDF 32 kb)
Supplementary Methods 2
Determination of the orbital part of the differential Hall coefficient (Equation 2) within the Kubo formalism. (PDF 44 kb)
Rights and permissions
About this article
Cite this article
Paschen, S., Lühmann, T., Wirth, S. et al. Hall-effect evolution across a heavy-fermion quantum critical point. Nature 432, 881–885 (2004). https://doi.org/10.1038/nature03129
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature03129
This article is cited by
-
Two-dimensional heavy fermions in the van der Waals metal CeSiI
Nature (2024)
-
Gate-tunable heavy fermions in a moiré Kondo lattice
Nature (2023)
-
Evidence for charge delocalization crossover in the quantum critical superconductor CeRhIn5
Nature Communications (2023)
-
Observation of Kondo condensation in a degenerately doped silicon metal
Nature Physics (2023)
-
Critical slowing down near a magnetic quantum phase transition with fermionic breakdown
Nature Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.