Abstract
Most mathematical models for the spread of disease use differential equations based on uniform mixing assumptions1 or ad hoc models for the contact process2,3,4. Here we explore the use of dynamic bipartite graphs to model the physical contact patterns that result from movements of individuals between specific locations. The graphs are generated by large-scale individual-based urban traffic simulations built on actual census, land-use and population-mobility data. We find that the contact network among people is a strongly connected small-world-like5 graph with a well-defined scale for the degree distribution. However, the locations graph is scale-free6, which allows highly efficient outbreak detection by placing sensors in the hubs of the locations network. Within this large-scale simulation framework, we then analyse the relative merits of several proposed mitigation strategies for smallpox spread. Our results suggest that outbreaks can be contained by a strategy of targeted vaccination combined with early detection without resorting to mass vaccination of a population.
Similar content being viewed by others
Main
The dense social-contact networks characteristic of urban areas form a perfect fabric for fast, uncontrolled disease propagation. Current explosive trends in urbanization exacerbate the problem: it is estimated that by 2030 more than 60% of the world's population will live in cities7. This raises important questions, such as: How can an outbreak be contained before it becomes an epidemic, and what disease surveillance strategies should be implemented? Recent studies1, under the assumption of homogeneous mixing, make the case for mass vaccination in response to a smallpox outbreak. With different assumptions, it has been shown2 that mass vaccination is not required. Policymakers must trade off the risks associated with vaccinating a large population8 against the poorly understood risks of losing control of an outbreak. Addressing such specific policy questions9 requires a higher-resolution description of disease spread than that offered by the homogeneous-mixing assumption and the differential-equations approach.
Here we present a highly resolved agent-based simulation tool (EpiSims), which combines realistic estimates of population mobility, based on census and land-use data, with parameterized models for simulating the progress of a disease within a host and of transmission between hosts10. The simulation generates a large-scale, dynamic contact graph that replaces the differential equations of the classic approach. EpiSims is based on the Transportation Analysis and Simulation System (TRANSIMS) developed at Los Alamos National Laboratory, which produces estimates of social networks based on the assumption that the transportation infrastructure constrains people's choices about where and when to perform activities11. TRANSIMS creates a synthetic population endowed with demographics such as age and income, consistent with joint distributions in census data. It then estimates positions and activities of all travellers on a second-by-second basis. For more information on TRANSIMS and its availability, see Supplementary Information. The resulting social network is the best extant estimate of the physical contact patterns among large groups of people—alternative methodologies are limited to physical contacts among hundreds of people or non-physical contacts (such as e-mail or citations) among large groups.
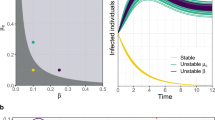
The case study we present is a model of Portland, Oregon, USA, but the approach is broadly applicable. People, in the course of carrying out their daily activities (such as work, study or shopping), move between several locations, both exposing themselves to infectious agents within these locations and transporting those agents between locations. We represent these processes by a social contact network, which can be represented as a bipartite graph, GPL, as shown by the example in Fig. 1a. For Portland, GPL has about 1.6 million vertices, with a giant component of about 1.5 million people and 180,000 locations. The degree distribution of the people vertices in GPL, that is, the number of people QPLj who visited j different locations, is shown in Fig. 2a. It has a sharp peak near the average value of about four different locations, followed by a fast, exponentially decaying tail. The degree distribution for the location vertices in GPL is very different, as shown in Fig. 2b. This is the number of locations MPLi having i different visitors during the day. The distribution has a power-law tail with an exponent of about -2.8.
a, A bipartite graph GPL with two types of vertex representing four people (P) and four locations (L). If person p visited location l, there is an edge in this graph between p and l. Vertices are labelled with appropriate demographic or geographic information, edges with arrival and departure times. b, c, The two disconnected graphs GP and GL induced by connecting vertices that were separated by exactly two edges in GPL. d, The static projections ĜP and ĜL resulting from ignoring time labels in GP and GL. People (such as 24-year-old male) are represented by filled circles, and locations (such as 34 Elm Street) by open squares.
a, The number of people QPLj who visited j different locations in the bipartite people–locations graph GPL. b, The number of locations MPLi in GPL that are visited by exactly i different people. The slope of the straight-line graph is -2.8. c, The number of people who have k neighbours in the static people–contact graph ĜP on log–log scale. d, The in and out degree distributions of the locations network GL. The slope of the straight-line graph is -2.8.
For many infectious diseases, transmission occurs mainly between people who are collocated (simultaneously in the same location), and spread is due mainly to people's movement. Hence we look at two natural projections of GPL obtained by drawing an edge between all pairs of vertices distance two from each other on the bipartite graph, as illustrated in Fig. 1b, c. The result is two disconnected graphs: GP, containing only people vertices, and GL, containing only locations. In GP, the edges are labelled with the sets of time intervals during which the people were collocated. For simplicity, however, we consider ĜP, a static projection of the time-resolved GP, obtained by discarding time labels, as shown in Fig. 1d. This is reasonable for diseases such as smallpox, severe acute respiratory syndrome or influenza, in which both the incubation period and duration of infectivity are of the order of several days, much longer than the 24-h approximate periodicity of people's contacts. This assumption introduces a systematic bias into results based on ĜP: the static projection yields a worst-case scenario of how the disease is likely to propagate, because ĜP is much more connected than GP. Any control strategy that is effective in such worst-case scenarios will also be effective in the time-resolved case. Furthermore, we have modelled the idea of an effective contact (one in which the transmission of disease is likely to occur) by removing from ĜP all edges for which the duration of contact was less than some minimum threshold, usually one hour. Even this thresholded version of ĜP is biased towards more connectivity than GP. An alternative to thresholding is to weight edges according to duration (and other factors affecting transmission). Figure 2c shows the degree distribution of ĜP for the Portland network. The other important projection of the bipartite graph is the locations network GL. If there is at least one person travelling from location l1 directly to l2 during the day, the two vertices corresponding to locations l1 and l2 are connected by a directed edge in GL from l1 to l2 that indicates whether the person is travelling in or out of the location. As before, we form a static version of the locations network, ĜL, by ignoring the time labels on the edges. The in and out degree distributions for the locations network are superimposed in Fig. 2d (ref. 12). The power-law decay evident there shows that ĜL is a scale-free network6 with an exponent of γ ∼ - 2.8. A simple explanation for this empirical observation is based on the capacity distribution of the locations in Portland. Land-use data indicate that the number of people using a location (its capacity) follows a power-law distribution with the same exponent γ. In large urban areas, people tend to fill locations up to their capacity. More densely filled locations (for example shopping malls) will have a larger number of people moving in from a proportionally larger number of other different locations (for example, homes), which in turn generates the scale-free character of ĜL with the capacity exponent γ.
Measurements of the average clustering coefficient (see Methods) for ĜP yield CP ≈ 0.48, and for ĜL, CL ≈ 0.04, both much larger than the roughly 10-6 of an Erdös–Rényi random graph with the same number of vertices and average degree5. This, together with the degree distribution and its small diameter (about 6), suggests that the people-contact graph is more like a small-world graph5 than a random graph. The clustering coefficient distributions versus degree13,14 shown in Supplementary Fig. 1 indicate that the locations network ĜL is an empirical example of a hierarchical scale-free structure15,16,17.
Both degree distribution and clustering are relevant to short-term propagation in a network, but longer time dynamics will be driven by global graph properties. It is thus natural to consider estimation schemes for global topological measures, such as expansion (see Methods). Informally, the higher the expansion, the quicker is the spread of any phenomenon (such as disease, gossip or data). We estimated an expansion value of about 2 for ĜP by random sampling, indicating that the people-contact graph is extremely connected. An immediate consequence is that, as for an assortatively mixed network18, ĜP cannot be shattered by removing (by means of vaccination or quarantine) a small number of high-degree vertices19,20,21,22. To verify this, we have computed the size of the giant component—the maximum number of people at risk for disease introduced by a single person—when all vertices of degree more than k are removed. A unique giant component persists even when all vertices of degree 11 and higher are removed, as shown in Fig. 3a. Thus, attempting to shatter the contact graph by vaccinating the most gregarious people in a population would essentially be equivalent to mass vaccination. Similarly, we show in Fig. 3b, c that closing the most-visited locations—or vaccinating everyone who visits them—does not shatter the induced people-contact graph until large fractions of the population have been affected. Other infrastructure networks exhibit very different shattering properties.
In a we remove (by vaccination or quarantine) all people with degree k and higher from the bipartite graph GPL. In b and c we remove all locations with degree k or higher from GPL and monitor the size of the largest connected component in the static people–contact graph induced by the remaining bipartite graph. d, Overlap ratios by degree. The lower curve shows the cumulative overlap ratio by degree, which is the overlap ratio for locations having degree k or less. The upper curve shows the overlap ratio for locations having degree exactly k.
Can epidemics be stopped without resorting to mass vaccination? Alternatives rely on early detection and efficient targeting. Here we introduce the overlap ratio, another non-local property of the graph that is crucial to early detection. Consider an idealized situation in which sensors at a location can detect whether any person there is infected. The feasibility of early detection depends on the number of sensors required to cover the population. This problem is equivalent to finding the minimum dominating set23. That is, we wish to find a subset L′ of locations so that all (or most) people visit some location in L′. The overlap ratio23 ω(J) of a set of locations J⊂L is n(J)/∑l∈Jdeg(l), where n(J) is the total number of people visiting any location in J, and deg(l) is the number of different people visiting location l∈J. The smaller the overlap ratio, the larger is the number of different locations in J visited by a single person. The overlap ratio by degree, shown in Fig. 3d, is the overlap ratio for the set Jk of locations having degree k. Clearly, not many people visit more than one high-degree location, which implies that the high-degree location vertices form a near-optimal dominating set. With high probability, early identification could be accomplished by using sensors placed at locations with the highest degree.
Alternatives to mass vaccination involve isolating and/or vaccinating small subsets of individuals to ensure that the disease will spread only locally in the graph. Most such strategies assume that people contacted by infectious people are the best candidates for vaccination or quarantine. However, it might also be possible to identify a good subset of the population to target before an outbreak. GP is composed of tight-knit communities joined by long-range edges. A model for this structure is given by adding long-range edges to random geometric graphs24. An infectious individual (even one with low degree) who travels can nucleate two independent growth centres. Other long-range travellers near these centres can in turn nucleate an exponentially growing number of growth centres, as demonstrated by the rapid worldwide spread of severe acute respiratory syndrome. Thus, targeting long-distance travellers (say, across town for urban regions) is a crucial component of any response.
Our results on the expansion property indicate that disease is likely to spread quickly if not controlled early enough. However, exactly how the number of casualties depends on response delay and what constitutes ‘early enough’ depend on disease-specific factors such as incubation period and probability of transmission, as well as scenario-specific factors such as the means of introduction. Because these dependences cannot be easily determined from an analysis of the static social network, we turn to simulation, which captures the full time-dependence of GPL (see Supplementary Methods for details).
There is not yet a consensus on models of smallpox. We have designed a model that captures many features on which there is widespread agreement9,25 and allows us to vary poorly understood properties through reasonable ranges1,2,26. Our model includes the following features: the incubation period is a gaussian truncated at 7 and 17 days with a 12-day mean and 2-day deviation; the prodromal period is 3–5 days; the infectious period is 4 days, during which infectivity decreases exponentially; death occurs 10–16 days after the rash develops in 30% of normal cases. Ninety-five per cent of susceptibles exposed for 3 h to a person at minimum infectivity will become infected (the remaining 5% have extremely high or low susceptibilities, mimicking some anecdotal transmission incidents); vaccination is assumed to be 100% effective before exposure, and it reduces the mortality and transmission rates when administered up to 2 days after exposure (or 4 days for a previously vaccinated person, assumed to be everyone over the age of 30 years). The model also includes haemorrhagic variants with a shorter incubation period that are 10-fold as infectious and invariably fatal (see Methods and Supplementary Information for details).
Note that EpiSims does not specify a value for R0, the basic reproductive number27. This parameter reflects how many people in a susceptible population are directly infected by the introduction of a single infective. R0 is a convolution of transmission rates and contact patterns, and EpiSims performs the convolution for us. The implied value of R0 is the ratio of the numbers of people in the first and original cohorts; that is, the number of people initially infected and the number infected directly by them. These estimates obviously include the effects of the simulated response strategy. For the set of experiments reported below, R0 ranges from 0.4 to 3.4.
In these scenarios, aerosolized smallpox was distributed indoors at busy locations over several hours, infecting of the order of 1,000 people. We assumed that the presence of smallpox was detected on the tenth day after the attack. Furthermore, we assumed that cases could be recognized in the prodromal phase after this date. We did not consider the confounding background distribution of influenza-like symptoms.
We studied the sensitivity of the number of casualties to three factors: mitigation efforts, delay in implementing mitigation efforts, and whether people move about while infectious. We simulated a passive (do nothing) ‘baseline’ and three active responses: mass vaccination covering 100% of the population in 4 days (‘mass’); targeted vaccination and quarantine with unlimited resources (‘targeted’); and the same targeted response, using only half as many contact tracers and vaccinators (‘limited’).
For a movie showing the spatial spread of disease under two different response strategies, see Supplementary Information. Figure 4 compares the efficacy of these strategies. For each strategy we plot (on a logarithmic scale) the ratio of the cumulative number of deaths by day 100 to the number initially infected. The absolute numbers are less important than the rank and relative sizes of gaps between the points. Also shown are the effects of delays of 4, 7 or 10 days in implementing the response. For each of the responses including the baseline, we allowed infected people to isolate themselves by withdrawing to the home. This could be due either to the natural history of the disease, which incapacitates its victims, or to actions taken by public health officials encouraging people to stay home. The results are grouped according to time of withdrawal to the home: (1) early, in which everyone withdraws before becoming infectious, producing the lowest estimates for R0; (2) late, in which everyone withdraws about 24 h after becoming infectious; and (3) never, in which everyone carries on their daily activities unless they die. The extreme cases are unrealistic but are shown here because they demonstrate the existence of a clear transition.
In this study, time of withdrawal to the home is by far the most important factor, followed by delay in response. This indicates that targeted vaccination is feasible when combined with fast detection. Ironically, the actual strategy used is much less important than either of these factors.
Methods
Clustering
Here we used the definition of the clustering coefficient, ci = 2ni/[ki(ki - 1)], given in ref. 5, which measures the extent to which neighbours of a vertex are connected by edges (ni is the number of connections between the neighbours of vertex i, and ki is the degree of i). Clustering has important implications for the rate and probability of disease spread4,28.
Graph expansion
The vertex expansion of a set P′⊂P is the ratio between the number of distinct vertices not in P′ reached through edges emanating from P′ and the number of vertices in P′, denoted by |P′|. Clearly, the vertex expansion of a set P′ with size |P′| = α|P| is bounded above by α-1 - 1. By definition, the vertex expansion of the graph GP is the minimum of the vertex expansions of all sets P′ with |P′| ≤ NP/2.
Haemorrhagic variants
In our model, haemorrhagic variants occur in 20% of pregnant women, 10% of HIV-positive people, and 2.4% of the population at large. Of those, 30% get an ‘early haemorrhagic’ variant, with a prodromal period between 0.5 and 1.5 days and an infectious period of 1 day (until death). Pregnancy and HIV status are assigned on the basis of demographics.
Simulation protocol
The protocol we simulated for targeted strategies was to place each prodromal person on a list. Contact tracers chose people at random from the list as they became available. We allowed 24 h for each contact tracer to vaccinate everyone living at the infected person's home and to travel to each location that the infected person visited, vaccinating a fraction of the people there who had been present when the infected person was there. We varied the fraction vaccinated according to the type of activity, from zero at a shopping location to unity at work and home. After 24 h the contact tracer was freed to service the list again. The infected person was sent to a quarantine location. In the ‘targeted’ case, roughly 20 people were vaccinated for each person initially infected. The peak rate was 10 people per day per initial victim, or roughly 10,000 people per day.
References
Kaplan, E., Craft, D. & Wein, L. Emergency response to a smallpox attack: the case for mass vaccination. Proc. Natl Acad. Sci. USA 99, 10935–10940 (2002)
Halloran, M., Longini, I. M. Jr, Nizam, A. & Yang, Y. Containing bioterrorist smallpox. Science 298, 1428–1432 (2002)
Kretzschmar, M. & Morris, M. Measures of concurrency in networks and the spread of infectious disease. Math. Biosci. 133, 165–195 (1996)
Keeling, M. The effects of local spatial structure on epidemiological invasions. Proc. R. Soc. Lond. B 266, 859–867 (1999)
Watts, D. & Strogatz, S. Collective dynamics of small-world networks. Nature 393, 440–442 (1998)
Albert, R. & Barabási, A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97 (2002)
Zwingle, E. Megacities. Natl Geogr. Mag. 202, 70–99 (2002)
Neff, J. M., Lane, J. M., Fulginiti, V. A. & Henderson, D. A. Contact vaccinia: transmission of vaccinia from smallpox vaccination. J. Am. Med. Assoc. 288, 1901–1905 (2002)
Ferguson, N. et al. Planning for smallpox outbreaks. Nature 425, 681–685 (2003)
Eubank, S. in Proc. ACM Symp. Appl. Comput. (eds Maniatty, W. & Szymanski, B.) 139–145 (ACM Press, New York, 2002)
Barrett, C. L. et al. TRANSIMS: Transportation Analysis Simulation System (Technical Report LA-UR-00–1725, Los Alamos National Laboratory, 2000)
Chowell, G., Hyman, J. M., Eubank, S. & Castillo-Chavez, C. Scaling laws for the movement of people between locations in a large city. Phys. Rev. E 68, 066102 (2003)
Dorogovtsev, S. N., Goltsev, A. V. & Mendes, J. F. F. Pseudo-fractal scale-free web. Phys. Rev. E 65, 066122 (2002)
Szabó, G., Alava, M. & Kertész, J. Structural transitions in scale-free networks. Phys. Rev. E 67, 056102 (2003)
Jin, E., Girvan, M. & Newman, M. Structure of growing networks. Phys. Rev. E 64, 046132 (2001)
Ravasz, E., Somera, A., Mongru, D., Oltvai, Z. & Barabási, A.-L. Hierarchical organization of modularity in metabolic networks. Science 297, 1551–1555 (2002)
Albert, R., Jeong, H. & Barabási, A.-L. Error and attack tolerance of complex networks. Nature 406, 378–382 (2000)
Newman, M. Assortative mixing in networks. Phys. Rev. Lett. 89, 208701 (2002)
Pastor-Satorras, R. & Vespignani, A. Immunization of complex networks. Phys. Rev. E 65, 036104 (2002)
Lloyd, A. & May, R. How viruses spread among computers and people. Science 292, 1316–1317 (2001)
Callaway, C., Newman, M., Strogatz, S. & Watts, D. Network robustness and fragility: percolation on random graphs. Phys. Rev. Lett. 85, 5468–5471 (2000)
Cohen, R., Erez, K., ben Avraham, D. & Havlin, S. Breakdown of the internet under intentional attack. Phys. Rev. Lett. 86, 3682–3685 (2001)
Eubank, S., Anil Kumar, V., Marathe, M. V., Srinivasan, A. & Wang, N. in Proc. ACM-SIAM Symp. Discrete Algorithms (ed Munro, I.) 711–720 (SIAM Press, Philadelphia, 2004)
Dall, J. & Christensen, M. Random geometric graphs. Phys. Rev. E 66, 016121 (2002)
Fenner, F., Henderson, D., Arita, I., Jezek, Z. & Ladnyi, I. Smallpox and its Eradication (World Health Organization, Geneva, 1988)
Eichner, M. & Dietz, K. Transmission potential of smallpox: estimates based on detailed data from an outbreak. Am. J. Epidemiol. 158, 110–117 (2003)
Keeling, M. & Grenfell, B. T. Individual-based perspectives on R0 . J. Theor. Biol. 203, 51–61 (2000)
Newman, M., Strogatz, S. & Watts, D. Properties of highly clustered networks. Phys. Rev. E 68, 026121 (2003)
Acknowledgements
We thank G. Korniss, G. Istrate and the Fogarty International Center at the National Institutes of Health for useful discussions, and acknowledge the work of all the members of the TRANSIMS and EpiSims team. The EpiSims project is funded by the National Infrastructure Simulation and Analysis Program (NISAC) at the Department of Homeland Security. The TRANSIMS project was funded by the Department of Transportation. H.G. was supported in part by the National Science Foundation (Division of Materials Research) and Z.T. by the Department of Energy. We thank the anonymous referees for their helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing financial interests.
Supplementary information
Related web sites
-
The EpiSims Project (Los Alamos National Laboratory): http://episims.lanl.gov
-
The TRANSIMS traffic simulation engine at Los Alamos National Laboratory: http://transims.tsasa.lanl.gov and also at http://www.transims.net
-
The Transportation Research Board (The National Academies): http://gulliver.trb.org
Background information and access to data and software
-
TRANSIMS
-
TRANSIMS bibliography
-
Social network estimates
-
EpiSims
-
Generic cities
Additional analysis of the social network
-
Clustering coefficient by degree
-
Location occupancies by activity type and time of day
-
Mixing rates by age
-
Local views of the social network
Methods: EpiSims modelling technology
-
Disease model
-
Transmission model
Methods: Smallpox modelling results
-
Parameters for smallpox
-
Simulated behaviour
-
Simulated response protocols
-
Modifications to the social network
-
Evolution of smallpox epidemics: snapshots
-
Evolution of smallpox epidemic: movie
Note on the degree distribution of a Random Geometric Graph
Future Directions
TRANSIMS
TRANSIMS is a large scale agent based traffic simulation tool being developed by The Los Alamos National Laboratory during the past 8 years involving a team of about 40 people and a total cost of 30 million US dollars. It is sponsored by the US DOT (Department of Transportation), US DOD (Department of Defense) and LANL (Los Alamos National Laboratory). TRANSIMS is a system capable of simulating second-by-second movements of every person and every vehicle through the transportation network of a large metropolitan area. IBM Business Consulting has created a commercial version of TRANSIMS, which is an integrated suite of products containing an easy-to-use Graphical User Interface for the modelling functions, a GIS-based network editor, a 3D data visualization and animation software, and a reporting system. They are releasing the latest version of TRANSIMS to both non-commercial and commercial users. The update includes the TRANSIMS-DOT Modelling Interface, the TRANSIMS-DOT Network Editor, the TRANSIMS-DOT Visualizer, and improvements to the TRANSIMS-LANL, Version 3 modules. IBM Business Consulting Services is preparing to assist the transportation planning and research communities in making the transition to this new technology. For information on how to receive TRANSIMS-DOT, please contact Naveen Lamba, IBM Business Consulting Services, Naveen.Lamba@us.ibm.com, Phone: 703-322-5656, http://www.transims.net
LANL has in the past offered an academic software license to TRANSIMS for a nominal fee. We intend to provide such a license for both the newest version of TRANSIMS and EpiSims. The Department of Transportation has announced that TRANSIMS will be available in mid-February, 2004 for academic use at a cost of around $1000 US.
More than half a dozen universities, including Texas A&M and Open University, already have such licenses. TRANSIMS has been used successfully by these universities to carry out transportation planning research. In addition, they have developed detailed semester long course material based on TRANSIMS for training transportation scientists. As an example, Professor Laurence R. Rilett, an associate research engineer with Texas Transportation Institute and the E.B. Snead II Associate Professor of Civil Engineering, at Texas A&M University been using TRANSIMS for the past five years. See http://itstexas.tamu.edu/presentations/2001annualmeeting/Rilett.pdf for a recent talk by Prof. Rilett on this topic. The TRANSIMS-LANL source code is also available to universities through Los Alamos for US$1000 for teaching, research and development. Contact Mr. Charles Gibson, gibson_charles_e@lanl.gov, in the Technology Transfer office. The computational resources required to develop a model for a city of a million or so people should be available at most universities.
The Federal Highway Administration and DOT have decided to use TRANSIMS as their primary transport planning modelling environment. This is an unprecedented step: the current models in use in Metropolitan Planning Offices (MPOs) are about 30 years old. It povides a perfect opportunity to produce social contact networks for various cities over the next 5-10 years time frame. IBM has been given the initial contract for this process and more than $100 million has been allocated for the initial deployment in 5-10 cities over the next 2-4 year time frame.
For more information and technical details on TRANSIMS see the bibliography below and proceedings volumes from the Transportation Research Board (TRB) annual conferences (http://gulliver.trb.org), where TRANSIMS has been regularly presented for the last eight years. These papers describe the entire spectrum of research: from modelling methods to efficient algorithms to studies and statistical analysis of data. The research papers and technical reports provide a very detailed account of methods and calibration processes used in TRANSIMS. Kai Nagel, who was our colleague at Los Alamos and currently is at ETH Zurich, is teaching a similar course at ETH and is also writing a book (http://www.sim.inf.ethz.ch/papers/) based on the work done at Los Alamos and ETH.
Calibration and validation of TRANSIMS has been carried out at various levels. A structural validation of the simulation is done so that the models produce known traffic invariants such as flow density patterns, jam wave propagation, etc. At the level of data matching, TRANSIMS is designed so that each module of TRANSIMS produces data sets that can be matched to known or collected macroscopic observables. These include: activities and population densities in an entire city, number of people occupying various locations in a time varying fashion, time varying traffic density split by trip purpose and various modal choices over highways and other major roads, turn counts, number of trips going between zones in a city, etc. The data set used for Portland has been validated at all these levels. TRANSIMS has been used in three 1-2 year case studies, for Albuquerque, Dallas/Ft. Worth, and Portland. Each of these studies guided its development to more sophisticated use cases. Technical reports on the Dallas and Portland case studies are available on LANL's TRANSIMS web site (http://transims.tsasa.lanl.gov).
TRANSIMS bibliography
Some of the published papers on different aspects of TRANSIMS are listed below. Many more papers, reports and user documentation for TRANSIMS are available on the web site: http://transims.tsasa.lanl.gov/documents.html
In particular, papers 9-18 set the theoretical and physical basis of the simulation itself. The other papers and publications are concerned with the computational problems of the simulation (such as efficiency of the algorithms, parallelization, etc.).
-
1.
C. Barrett, K. Bisset, R. Jacob, G. Konjevod, M. V. Marathe. Classical and Contemporary Shortest Path Problems in Road Networks: Implementation and Experimental Analysis of the TRANSIMS Router, in Proceedings of the European Symposium on Algorithms, Lecture Notes in Computer Science, Springer, 126-138, 2002.
-
2.
C. Barrett, R. Jacob, M. V. Marathe. Formal-Language-Constrained Path Problems. SIAM Journal of Computing, 30 (3): 809-837, 2000.
-
3.
R.R. Jacob, M. V. Marathe, K. Nagel. A Computational Study of Routing Algorithms for Realistic Transportation Networks, ACM Journal of Experimental Algorithms, 4 , Article No. 6 (1999).
-
4.
P. Wagner and K. Nagel., Microsimulation and the Physical Basis for TRANSIMS. Microscopic Modelling of Travel Demand: The Home-to-Work Problem, Transportation Research Board Preprint, (1999).
-
5.
P M Simon and K Nagel, Simple queuing model applied to the city of Portland, International Journal of Modern Physics , 10, 941-960 (1999).
-
6.
J. Esser and K. Nagel, Census-based travel demand generation for transportation simulations. In Traffic and Mobility: Simulation-Economics-Environment, Eds. W. Brilon, F. Huber M. Schreckenberg, H. Wallentowitz, Springer, (1999), p. 135-148.
-
7.
K. Nagel, M. Rickert, P. M. Simon and M Pieck. The dynamics of iterated transportation simulations. Presented at the TRIannual Symposium on Transportation ANalysis (TRISTAN-3), San Juan, Puerto Rico, (1998).
-
8.
M. Rickert and K. Nagel, Issues of simulation-based route assignment, International Symposium on Transportation and Traffic Theory (ISTTT) (1999).
-
9.
T P Kelly and K Nagel. Relaxation criteria for iterated traffic simulations, International Journal of Modern Physics C, 9, 113-132 (1998).
-
10.
P M Simon, K Nagel, Simplified cellular automaton model for city traffic, Physical Review E, 58, 1286-1295 (1998).
-
11.
K Nagel, D E Wolf, P Wagner, and P Simon, Two-lane traffic rules for cellular automata: A systematic approach, Physical Review E, 58, 1425-1437 (1998).
-
12.
K Nagel. Experiences with iterated traffic microsimulations in Dallas, Overview Paper, in Traffic and Granular Flow , (1997).
-
13.
M Rickert, K Nagel. Experiences with a simplified microsimulation for the Dallas/Fort-Worth area, International Journal of Modern Physics C, 8, 1009 (1997).
-
14.
K Nagel, C L Barrett. Using microsimulation feedback for trip adaptation for realistic traffic in Dallas, International Journal of Modern Physics C, 8, 505-525 (1997).
-
15.
P Wagner, K Nagel, D E Wolf, Realistic multi-lane traffic rules for cellular automata, Physica A, 234, 687-698 (1997).
-
16.
M. Rickert, K. Nagel, M. Schreckenberg and A. Latour. Two lane traffic simulations using cellular automata, Physica A, 231 (4) 534-550 (1996)
-
17.
K. Nagel, Particle hopping models and traffic flow theory, Physical Review E, 53 (5), 4655 (1996).
-
18.
K Nagel and S Rasmussen. Traffic at the edge of chaos, Artificial Life IV, edited by R.A. Brooks and P. Maes, MIT Press Cambridge MA, p. 222-235, (1994).
Social network estimates
An instance of the static people-people referred to in the paper can be downloaded here. This is an ASCII text file compressed with gzip. For each vertex, it gives the vertex id and degree, followed by a list of its neighbour's identifiers and the duration of contact with that neighbour in hours. For example, the data for the first two vertices in the file is:
Vertex (person) id 63470 has 7 neighbours. Neighbour 30497 had 3.25028 hours of contact with 63470 during the course of a day. Neighbour 63471 is the second vertex in the file. Note that each link is reproduced twice in this file: once for each endpoint.
The full bipartite dynamic social network data can be obtained from LANL by sending an e-mail request to episims-data@lanl.gov accompanied by a one page, formal proposal for the use of the data. This data contains the following information: for every person (approximately 1.6 million of them) characterized by an integer index, it lists during a 24 hour period the entrance times and exit times into and from a location (characterized by a location integer index), for all locations that person visited during the day (there are a total of approximately 181,000 locations in the Portland data). The data is too large to download via the internet (approximately 12GB) but it will be sent via mail to researchers upon our acceptance of the proposal. This is for a single-day population activity. As more network instances are generated, we intend to make them available throgh the same mechanism.
The census data that goes into the TRANSIMS simulation is publicly available from the census bureau at www.census.gov. Land use and survey data are typically held by urban planning organisations. The Department of Transportation lists data resources and contact information for the 35 largest US urban areas at http://tmip.fhwa.dot.gov/clearinghouse/docs/landuse/compendium/iurd.stm.
EpiSims
The EpiSims software is not as mature as TRANSIMS. It is research software subject to almost daily change and lacking a user interface. We intend to create a stable, documented version covered by an academic license similar to that for TRANSIMS. In the meantime, we have included in this Supplementary Information details on the modelling technology and the parameters used for our studies sufficient for the motivated reader to reproduce our models.
Generic cities
As we have tried to make clear in this paper, we view the social networks created by TRANSIMS as a single instance of a stochastic process defined in an enormous space of possibilities. Our work on characterizing this instance has been undertaken with the goal of eventually generating, through a generalized random graph process, graphs that are constrained to look like social networks produced by the TRANSIMS data. Preliminary studies show that indeed it is possible to parameterize the process in such a way as to model specific cultural, geographic, or demographic attributes of cities. The study, along with the network data will be posted on the EpiSims web site in the near future.
Additional analysis of the social network
The following is a list of a number of other measurements based on the social network data.
Clustering coefficients by degree

Figure 1a
(GIF 21,3 KB)
Clustering coefficients by degree for a) the people-contact graph and b) the locations network (after discarding the direction of edges in the latter).

Figure 1b
(GIF 23,7 KB)
Occupancies by activity type and time of day

Figure 2a
(GIF 8.38 KB)
Each location in EpiSims is associated with several activities. We consider the primary activity for each location (namely the activity done by the majority of people visiting that location) and observe the number of people with this activity at the location (i.e., temporal degree), as time progresses. The figures above show the temporal degrees of a few locations with different activity types. Each plot shows the temporal degree of 5 randomly chosen locations. The horizontal axis shows time over a 24 hour period with 0 being approximately 11:00 p.m. The primary activity is indicated in the figure. The vertical axis represents the number of individuals at that location as the day progresses. The temporal degrees are according to our expectations. For example, figure a) shows 5 different randomly chosen location blocks labelled homes: the degree decreases considerable during mid-day when people leave for work then it goes back up when they start returning home (some people do not return home working night shifts and leading to a small difference compared to the early morning hours). The locations where the primary activity is work, fill up with people during mid-day, to get emptied again by night when they leave, see figure b). The little dips around noon correspond to people leaving workplaces for lunch. Similarly, for schools, figure e) and colleges figure f) there is a mid-day fill up, with the difference that in colleges the evening classes create a second peak. All these data are result of the people mobility generated by the TRANSIMs simulation engine, and thus they are not inputs to the simulation. The fact that these curves follow our expectations, is a validation of the simulation.

Figure 2b
(GIF 8.31 KB)

Figure 2c
(GIF 8.31 KB)

Figure 2d
(GIF 9.43 KB)

Figure 2e
(GIF 8.58 KB)

Figure 2f
(GIF 9.95 KB)

Figure 2g
(GIF 9.95 KB)

Figure 2h
(GIF 10.8 KB)
Mixing rates by age


Figure 3a
(GIF 8.68 KB)
Demographics are likely to play a very important role in determining the efficacy of any strategies for disease control. We show here mixing rates for one important demographic group, age. Figures a) - o) show the average number of contacts that a particular age group has with the rest of the population. Each graph corresponds to a specific age group (say A). The horizontal axis corresponds to all the age groups. For a particular age group (say B) on the x-axis, the (corresponding) value of the vertical axis corresponds to the average number of contacts group A make with group B. The particular age (A) for which results are plotted is stated above the plot. The empirical observations agree quite well with our intuition. It also shows the degree of mixing among parts of population with that belong to various age groups. From the pictures a) - g) it follows that youngsters typically have meetings with youngsters (siblings, schools, etc.). Figures i) - o) show that adults spend most contact with other adults (work places). The very high peaks in f), g), and i) show that teenagers have most contacts among other teenagers of the same age (16-18), and have little mixing with others. One reason for studying these distributions is to see if it is possible to design targeted vaccination strategies that are derived from the demographic attributes of a population. Mixing properties among various age groups help specialize the targeting methodology.

Figure 3b
(GIF 8.80 KB)

Figure 3c
(GIF 8.79 KB)

Figure 3d
(GIF 8.49 KB)

Figure 3e
(GIF 9.78 KB)

Figure 3f
(GIF 8.74 KB)

Figure 3g
(GIF 9.78 KB)

Figure 3h
(GIF 10.2 KB)

Figure 3i
(GIF 10.2 KB)

Figure 3j
(GIF 9.8 KB)

Figure 3k
(GIF 10.1 KB)

Figure 3l
(GIF 9.95 KB)

Figure 3m
(GIF 10 KB)

Figure 3n
(GIF 10.4 KB)

Figure 3o
(GIF 10.9 KB)
Local views of the social network

Figure 4a
(GIF 130 KB)
These figures display different representations of the same small part of the person-person contact graph, rendered using the Tulip graph (http://www.tulip-software.org) drawing program. Vertices represent individual people, and edges are present if the two people came into contact for at least an hour during the day. Vertices are coloured by their distance in the graph from one of a few individuals. Vertex colours are the same in each panel. Edges are coloured corresponding to the colour of vertices at either end.

Figure 4b
(GIF 36.5 KB)

Figure 4c
(GIF 115 KB)

Figure 4d
(GIF 59.6 KB)
EpiSims Modelling Technology
EpiSims is designed to simulate many different diseases. Hence we have developed a disease model capable of representing the characteristics of many diseases by appropriate parameter selection. Here we describe the general within-host progression and between-host transmission models used for the study results reported below, together with the actual parameter settings used in the smallpox and plague models. In addition, we describe a planned revision of the models to address limitations of the current models.
Disease Model
Within Host
Each individual in the simulation who is exposed (either through exposure to an initial release or through contact with an infected and infectious person) will progress through a series of disease stages. An exposed individual will either become infected or not with a probability based upon the disease model and the individual's demographics. Individuals who become infected either develop a clinical case of the disease or not. For instance, some fraction of those infected with smallpox never develop a fever or symptoms of the disease. As above, the probability of developing clinical symptoms depends upon victim characteristics.
Those individuals who develop clinical cases may develop different variants of the disease with correspondingly different disease courses and different epidemiological implications. Five different manifestations of smallpox (infection with variola major) are identified in the literature:
-
ordinary,
-
modified,
-
flat or malignant,
-
early hemorrhagic,
-
and late hemorrhagic.
EpiSims uses a single parameter, the disease load, to represent the effect of a disease upon a host. The load in EpiSims is intended to be analogous to viral titre in a throat swab, number of spores or bacteria present, concentration of toxin, etc. However, it need not reproduce such clinical aspects of these loads as distribution throughout the body. It is merely a parameter that is used to determine whether a person is infected, symptomatic, too sick for normal activities, infectious, or dead. The higher the disease load, the sicker the person.
An isolated contaminated person or location's load grows or shrinks at predetermined rates. All locations share a single common exponential growth or decay rate, specified by the user in the disease description. For example, the amount of virus present in the environment would decay exponentially if there were no sources (infected people); the amount of bacteria might grow exponentially; while the number of spores would remain fixed.
Each person has his or her own schedule determining the growth and decay of the disease. The schedule provides for piecewise exponential change in the load (or, put another way, piecewise linear growth of the logarithm of the load). The growth schedule is parameterized by an arbitrary number of time delays (t0, t1, t2, ...) and growth rates (ɣ0, ɣ1, ɣ2, ...). Any of the growth rates can be zero or negative if desired. We use this growth schedule to represent many different effects, including:
-
small variations in host response to a disease, by drawing growth rates from a distribution where the data is available;
-
different variants of disease caused by the same infectious agent, e.g. hemorrhagic or malignant smallpox;
-
immuno-compromised individuals;
-
vaccination or application of anti-virals or antibiotics;
-
variations in infectivity during the course of the disease.
The final component of the within-host disease model is a set of threshold values for determining the effect of the load on an individual. The thresholds we use determine whether an individual is:
-
infected (LI),
-
symptomatic (LS),
-
staying home from normal activities (LHS),
-
infectious (LC),
-
or dead (LD).
It is important to note that EpiSims does not assume any ordering of these values, except that LD is the largest and LI the smallest. Thus the relative value of the "staying home" and infectious thresholds can dramatically alter the course of the simulation, as it should. On the other hand, the thresholds in this model are global values, so there is no individual variation in disease related behaviour.
The course of an individual case of disease in EpiSims runs like this:
-
A person absorbs load from the environment.
-
As long as the load is below the threshold for infection, it does not grow. It may in fact decrease.
-
When the absorbed load crosses the threshold for infection, it begins to grow exponentially at the rate ɣ0. Absorption from the environment continues, but is soon negligible compared to the exponentially growing load within the host.
-
After t0 hours of growth at the rate ɣ0, the rate changes to ɣ1. These changes continue through the last time delay specified for the individual.
-
When the load is above the symptomatic threshold, other people in the simulation, such as contact tracers, can recognize that the individual is sick.
-
When the load is above the "stay at home" threshold LHS, the individual will return home and not leave unless quarantined.
-
When the load is above the infectious threshold LC, the individual begins to shed a fixed fraction of load to the local environment per hour. Typically, this fraction is negligible compared to the person's load.
-
If the load crosses the death threshold, the individual is removed from the simulation.
Transmission model
Environment-mediated transmission
In EpiSims, an infectious person contaminates his or her environment, in a process analogous to sneezing or coughing. The contamination may be restricted to a small region near the infected person, and/or it may spread to an entire EpiSims location, which is roughly the size of an apartment building, office building, or shopping mall. Transmission occurs as uninfected people absorb virus (or bacteria, spores, etc.) from a contaminated location.
Geographical locations, as well as people, have a disease load associated with them, representing the level of contamination of the location. Disease load in a location has an associated exponential growth rate, which may be positive, negative, or zero. This allows EpiSims to model non-infectious diseases, transmission of disease between people who are never in direct contact, or diseases with non-human vectors. The simulation can be initialized by contaminating a specific location at a specific time and/or by assigning a non-zero load to one or more people.
Disease transmission among people is accomplished by contaminating the environment they share. There are two steps:
-
1.
infectious people contaminate their local environment by shedding load.
-
2.
people present at a contaminated location absorb load from it.
There are two corresponding parameters controlling the interaction of each person with his or her local environment:
-
1.
shedding rate, ßS, the fraction of the individual's load that is shed to the environment per hour.
-
2.
absorption rate, ßA, the fraction of the environment's load that is absorbed by an individual per hour.
These parameters are specific to the individual. In this way EpiSims can model some behavioural differences that affect transmission rates. For example, children can be given higher absorption and shedding rates than adults if the available data so indicate.
The shedding and absorption parameters can be set from an estimate of how long a person must be in close contact with an infectious person before becoming infected. The product of the shedding rate and the threshold for contagion (ßSLC) gives the minimum amount of load transferred from the infectious person to the environment per hour. The product of the absorption rate with the shedding rate and the threshold load for contagion (ßA ßS LC) gives the overall rate of absorption by the exposed person. The minimum time to become infected is the threshold for infection divided by the overall absorption rate, or min(TI) = LI/ßA ßS LC. If more detailed information is available, for example the probability of infection as a function of time spent in close contact with an infectious person, it can be incorporated into the model.
The scaling of transmission probability with number of susceptibles is not well understood. Clearly, a single infectious person is unlikely to infect everyone in a large stadium, although she or he might infect everyone in a household. Yet the same person might infect everyone in a conference room. The mechanistic transmission model we have outlined here has the property that an infectious person infects roughly the same absolute number of people per unit time, regardless of the number of susceptibles present. This is because load is absorbed from the environment in a round robin fashion, and it is removed from the environment by absorption. Once a person has absorbed enough load to be infected, that person no longer absorbs load. This models diseases for which the primary caregiver is most likely to be infected and people who are not in close contact are unlikely to be infected.
The transmission model in EpiSims can reflect both the distance between a susceptible individual and an infectious person and the duration of the exposure. If the interaction is of sufficient duration given the distance at which it occurred, the susceptible individual is assumed to have been exposed.
Because of the limitations of the process that produces our social network estimates, we do not have data for proximity of people, other than that they are in the same (possibly very large) location. We do have good estimates of the duration of contact. It seems as though the dependence on distance is very coarse: one mode of transmission occurs for close ranges (< 6 feet) and another for larger distances. We have developed an ad hoc model that takes advantage of this coarseness. A large location is split into small sublocations. An infectious person transmits disease to everyone in the same sublocation at a much higher rate than to others in different sublocations of the same location.
Basic reproduction number
Traditionally, epidemiology has focused on the basic reproduction number, a measure of how many people would be directly infected by a single infectious individual inserted into a population of susceptibles. The basic reproductive number is a convolution of several quantities evaluated at the introduction of the first infectious person:
-
a (possibly demographic-dependent) person-person transmission rate,
-
the mixing rate,
-
the number of susceptibles.
Indeed, it is possible to define a spectrum of reproductive numbers related to the characteristic directions in the space of demographics along which disease spreads. In addition, the same convolution of quantities taken at other times will in general yield a time varying reproductive number. The reproductive number is not an input parameter for EpiSims. Instead we suggest that the demographic-dependent person-person transmission rates are the most easily observable invariant quantities, and allow the simulated movement of people to produce the time dependent mixing rates. For diseases with fairly lengthy incubation periods, and thus clearly distinct waves of infection, a value for the basic reproductive number can be estimated from EpiSims output as the ratio of the size of the first two cohorts infected in the simulation.
Smallpox Modelling Results
We have chosen disease parameters for this study based on data available in the open literature, particularly Fenner et al. (Smallpox and its eradication, F. Fenner, D.A. Henderson, I. Arita, Z. Jezek, I.D. Ladnyi, World Health Organization, 1988, also available online (http://www.who.int/emc/diseases/smallpox/Smallpoxeradication.html), and on private communications with many experts in smallpox modelling. There are, of course, differences of opinion on the correct value of many of these parameters. The ranges of values we have chosen represent our understanding of the best estimates available at the time the studies were undertaken. Our intention with this model is to demonstrate the range of possibilities available in individual based models, and to conduct sensitivity studies for certain parameters.
Parameters for smallpox
It is not sufficiently precise to say an individual has smallpox, because each manifestation has a distinct disease course and poses a different set of issues for response. For example, the flat and hemorrhagic forms disproportionately affect pregnant and immuno-suppressed individuals. Patients with these forms have shorter prodromal periods, are more highly infectious, and will present with different symptoms than ordinary smallpox patients. The correlation between these differences is particularly unfortunate -- if enough people are exposed to the virus, it is likely that individuals with these short incubation time forms of smallpox will be the first to show up in the health care system. They will be haemorrhaging from all body orifices and progressively under every inch of their skin and they will die at a much higher rate than those with ordinary smallpox. Because their symptoms are not as obvious as the classic pox and there will not yet have been any diagnoses of ordinary smallpox, they are likely to be misdiagnosed at first. Misdiagnosis is particularly dangerous in these cases, as they are highly infectious almost as soon as they start presenting symptoms (much sooner than ordinary smallpox patients). Our model for smallpox attempts to capture some of these correlations and provide for the possibility that a subpopulation such as immuno-compromised people might serve as a backbone for disease transmission.
The transmission model quantifies the types of interaction necessary for a susceptible individual to be classified as exposed to a disease and potentially infected with it. In this context we define exposure to mean that the individual has received enough smallpox virions or viral particles that he or she could develop smallpox. Although the threshold is commonly taken to be a single virion for smallpox, not everyone who is in proximity to an infectious person will receive this dose. For example, CDC guidelines recommend prioritizing for vaccination people who have had "face-to-face close contacts ( ~6.5 feet or 2 meters) or household contacts to smallpox patients after the onset of the smallpox patient's fever." (CDC Interim Smallpox Response Plan and Guidelines, Draft 2.0 - 11/21/01) They also distinguish among non-household contacts with fewer than 1 hour of contact, 1-3 hours of contact, and more than 3 hours of contact. Thus, we chose to set transmission parameters so that 1 hour of contact was often sufficient to infect, and more than 3 hours of contact almost always sufficient.
Several variables affect the relationship between exposure and the duration and distance characterizing the interaction between the infectious person and susceptible individual. For example, it is well known that smallpox victims tend to be most infectious during the first few days of rash, with contagion diminishing as the disease progresses. Different manifestations of smallpox (e.g. modified, ordinary, flat, early hemorrhagic, or late hemorrhagic smallpox) also imply different levels of transmissibility. Consequently, a smallpox transmission model should take into account the particular disease manifestation present in the infectious person.
We have chosen to represent two variant forms of the disease, both caused by variola major: ordinary smallpox and hemorrhagic smallpox, which is both more infectious and more lethal. Tables 2 and 3 shows parameter values for the two variants. Note that the variant manifested by each person is determined before the simulation is run. We assign 2.4% of the general population hemorrhagic parameters, as well as 21% of pregnant women, and 10% of HIV cases (which are drawn uniformly from the population independent of demographics at a rate of 0.14\%).
The growth rates and time delays for ordinary smallpox are chosen so that the following hold:
-
The incubation period is normally distributed about 12 days, with a standard deviation of 2 days. The distribution is thresholded at 7 and 17 days. That is, any incubation periods initially chosen to be less than 7 days are reassigned the minimum value of 7 days, and similarly for periods longer than 17 days. At the end of this period, the person is in the prodromal phase of the disease, with non-specific symptoms of fever and rash.
-
The threshold for becoming infectious is reached after an additional period of 4 days with probability 0.8, or 3 or 5 days with probability 0.1 each.
-
Upon crossing the threshold for contagion, the individual rapidly (in 12 hours) reaches a peak contagion in which he sheds 10 times as fast as the minimum rate.
-
Contagion gradually decays over the course of 4 days (with probability 0.8), or 3 or 5 days, each with probability 0.1.
-
6 - 12 days (chosen uniformly at random) after the end of the period of contagion, 30% of victims (45% of pregnant victims) die:
-
Post exposure vaccination can prevent death if administered up to 2 days after exposure, or up to 4 days for people over 30 (who are assumed to have been vaccinated previously). In addition, it ameliorates the disease.
The parameters for the hemorrhagic variant are adjusted so that all victims die. 30% of the deaths occur between 12 hours and 36 hours after the end of the incubation period (modelling an early hemorrhagic variant); the rest are 5-7 days after the incubation period. Post exposure vaccination has no effect on people who develop a hemorrhagic variant.
Variola is assumed to be inactivated very quickly in the environment, so that direct contact is required for transmission. Its decay rate outside a host is taken to leave only one virion in a million viable after an hour.
As discussed above, EpiSims requires shedding and absorption rates for each person to accomplish disease transmission. For the disease parameter values given in the tables above, shedding rates of ßS = 10-4 per hour for people with normal variety and 10 times higher for the hemorrhagic variety, that involves more coughing, are reasonable. The absorption rate can now be determined using estimated transmission probabilities as a function of time. For example, assume that 1 hour of close contact with an infectious person leads to infection in 95% of the people. The remaining 5% will become infected in durations spread uniformly from 3 minutes to 18 hours, as shown in Table 3.
There are several possibilities for choosing whom to infect. The load could be spread among everyone present, concentrated onto one victim, or anything in between. For the studies reported in this paper, environmental load was distributed among all present, though it had no effect on those who were immune.
Although not directly parameterized, EpiSims can control the infectivity ratio defined as the quotient of peak infectivity at the beginning of the infectious period to minimum infectivity, given by the threshold for contagion, $L_C$. In the experiments reported here, the ratio is 10.
As noted above, R0, the basic reproductive number, is not a parameter of this model. R0 depends on the social network, disease transmission parameters, and the identities of the first infected people. We can estimate a value from the results of each simulation run as the ratio of the number of people in the second cohort of infected people to the number in the first cohort. With the parameters listed herein, varying the initially infected people and the viral load that causes people to stay home sick, estimated values for R0 vary from 1.0 to 3.4.
Simulated Behaviour
One of the most important assumptions in any smallpox model is whether infectious people are mixing normally in the population. There are two relevant questions: can infectious people be diagnosed by the casual observer (i.e., are people infectious before the appearance of characteristic pox?); and are people incapacitated before they become infectious? This study was designed to examine the sensitivity of results to variation in this assumption. We undertook to model two (probably unrealistic) extreme cases: one in which no one who is infectious is mixing with the general population and another in which no one's behaviour is affected at all by the disease. In addition, we modelled one more realistic case between these two extremes. We have not explored more of this variability because we would first like to refine the overall model.
Table 1 shows parameter values for disease thresholds. We have examined three different thresholds for staying home sick, or self-isolation. The effect of the values we have chosen is as follows:
-
early: people are at home when they become infectious
-
late: People engage in their usual activities for a while after becoming infectious. Because of the way this has been implemented, we do not have direct control over the distribution of durations. For the value we have chosen, 70% of people continue their usual activities for 5 hours or less after becoming infectious; 90% for 2 days or less.
-
never: people effectively do not isolate themselves
Simulated Response Protocol
Every person who becomes symptomatic in the simulation is placed on a list. Every simulated day, if contact tracing is in effect, a subset of the people on the list is chosen for contact tracing. The subset contains the minimum of an absolute number of people or a fraction of the people on the list. In the experiments reported here, we use the fraction 0.8 and set the absolute threshold at either 10,000 or 1,000. These are probably unrealistically large numbers, but they allow us to estimate the best case results of a targeted vaccination strategy. Note that because vaccination is done on a household basis, the actual number of people vaccinated per day can be several times as large as the absolute threshold.
We consider the effects of delay in response, assuming the response is instituted 14, 17, or 20 days after the attack. Mass vaccination is assumed to require four days.
Social network
The activity data currently available from TRANSIMS resolves locations at which activities are performed down to roughly four per city block. Using the social network derived from this level of resolution creates unrealistically high contact rates. Instead EpiSims breaks each location into several cells. Individuals are assigned to one of the cells containing other people performing similar activities at that location. The maximum number of people allowed in a cell varies by activity type, as shown in Table 7. The values chosen below are nothing more than reasonable guesses. The larger these values, the more opportunity for mixing and transmission.
1) Evolution of smallpox epidemics

Figure 5a
(GIF 355 KB)
Above are four frames of a movie showing a side-by-side comparison of a baseline case (on the left) with a targeted vaccination and quarantine strategy, in which symptomatic people are interviewed, most of their recent contacts identified, and the contacts and their households are vaccinated and sent to quarantine. The full movie below shows 6 frames per day at 4 hour intervals for 70 days. The bars represent number infected at each location, and the colour represents the fraction of infected people who are infectious. The attack is presumed to be covert, so until people become symptomatic around day 10 they continue with their normal activities (and there is no difference between the two movies). The attack site, a university, is readily visible as a very large spike in the downtown area which grows and decays every day as students gather on campus and disperse throughout the city. Above the views of Portland are strip charts displaying the cumulative number of people infected and dead as a function of time, and for the targeted response, the number vaccinated and quarantined, which are important for determining feasibility of the response. These are not labelled, but the colour coding corresponds to the labelled text below the charts. Note that the scale on the leftmost chart is a factor of one hundred different from the rightmost.

Figure 5b
(GIF 377 KB)

Figure 5c
(GIF 377 KB)

Figure 5d
(GIF 375 KB)
Smallpox propagation movie (MOV 250 MB)
(If your browser is not set up to play movies, try opening the AVI file directly with Windows Media Player or QuickTime Player.)
Note on the degree distribution of a Random Geometric Graph
A random geometric graph (RGG) is obtained by randomly distributing points in the unit square and connecting with edges only those points which are within a distance R of each other. The existence of a peak around the mean degree and an exponentially decaying tail for large degrees comes from the fact that physical proximity has a typical cost to it, requiring time and space, and a person simply cannot be in close proximity to 1.6 million people during the day14. In spirit, an RGG is similar: the distance R represents a cost beyond which edges do not exist (one can relax this by introducing a distribution around R).
Future Directions
As a result of discussions with modellers and epidemiologists, we have identified several areas in which the current EpiSims technology needs improvements. The design below will permit much easier comparison with other models in the field while still retaining the individual based resolution characteristic to EpiSims. The remainder of this section consists of excerpts from a design document. It does not represent the current state of EpiSims.
Requirements for a model:
-
allow multiple manifestations of disease, possibly based on demographics
-
allow contamination of locations
-
allow variable infectiousness and susceptibility
-
represent effects of a variety of treatments
-
relate transmission rate to duration/type of contact and demographics of susceptible and infectious
-
allow flexible ordering of symptomatic, infectious, etc.
-
allow flexible transmission scaling behaviour as number of people increases
-
label states with meaningful names (infected, symptomatic, etc.)
-
provide easy tracking of state changes
-
scale to populations of 10 million
Desirable properties:
-
easy matching between people and the course of their disease
-
match state update process to discrete event system
-
entire model and scenario specifiable by naive user
-
lightweight computation and memory requirements
Drawbacks of the current model:
-
thresholds affect both infectiousness and progress of the disease, with complicated consequences
-
large variability in state duration arising from small variability in initial load
-
poor decomposition of infection rate by demographics
-
unwarranted precision in model
-
profusion of exponentiation and logarithms, slowing computation
-
approximates nonlinear dynamics with linear dynamics
-
overly deterministic transmission process
Benefits of the current model:
-
easy mechanism for contaminating a location
-
analogous to physical process
-
mechanism for representing effects of treatment
-
transmission independent of number of people in a location (not always a benefit!)
Different individuals manifest infection by the same infectious agent in different ways. A primary goal of EpiSims is to capture the dependence of disease manifestation on demographics. To this end, each person in the population is assigned:
-
a Disease Manifestation,
-
a Disease State and an associated time stamp,
-
a Treatment Id,
-
and a Disease Transmission Type.
The assignment is consistent with user specified probabilities conditional on demographics. A variety of assignments may be produced by varying the random seed. During the course of the simulation, each location (at the finest resolution simulated) is also associated with a disease state. Some aspects of a location's disease state may be modified by exogenous events created by the user (e.g. contamination, decontamination); others reflect transmission dynamics internal to the simulation.
In addition to the conditional probabilities for the assignments described above, the user must also specify the following:
-
a set of Disease Manifestations,
-
a set of Transmission Rate functions,
-
a set of behavioural threshold values.
Planned implementation of Disease Manifestations
Each possible Disease Manifestation must be specified by the user prior to using EpiSims. A Disease Manifestation is a Markov Chain consisting of a finite set of Disease States together with transition probabilities among them and a distribution of residence times in each state. Most Disease States are associated with values for the following attributes relevant to the spread of disease:
-
prodrome (non-specific symptoms, easily mis-diagnosed)
-
symptoms (depending on thresholds)
-
infectivity (capable of transmitting disease - may also represent contamination)
-
incapacitation (cannot perform some activity - distinct from symptoms)
The value of some attributes affects the dynamics of disease transmission directly. For example, infectivity is related to the probability of transmission as explained below. Others may affect the behaviour of an infected person: symptom levels reflect the severity of symptoms, the likelihood of health-care-seeking behaviour, and the likelihood of correct diagnosis; the degree of incapacitation affects whether a person stays home from work, shopping, or other activities. Detailed interpretation of these attributes is provided below. In addition to these attributes, the user can assign each state a unique name. Simulation outputs and analysis tools will refer to states by this name.
Note that the Disease State does not contain a "recovered" attribute. The simulation maintains information about each person's history, including whether an individual has ever been infected and whether he or she is currently infected. These can be combined into the notion of "recovered". Alternatively, it is possible to specify a transition from one Disease Manifestation to another upon "recovery". That is, a person who has contracted the disease and recovered may have a different reaction the next time.
As mentioned above, the finest resolution of location also includes a form of Disease State. A location's Disease State contains enough information to represent contamination. Thus, at least the "infectivity" attribute of a Location's Disease State should be maintained, although other attributes are ill defined. Possibly, the "symptom" attribute could be used to specify whether contamination could be detected. Note that, unlike a person's Disease State, a Location will probably cycle through many infections in the course of the simulation. Whenever an infectious person is present, the Location will become contaminated. This contamination may decay quickly if the residence time in the infected state specified by the user is short.
Residence Times
Every Disease State except the special dead and uninfected states is associated with a probability distribution of residence times. The user may choose from a predetermined set of distributions and assign any necessary parameters.
State Transitions
The user may specify an arbitrary number of transitions out of each Disease State into others. Associated with each transition is a probability. Optionally, each transition may also be associated with a set of Treatment Ids. When a person leaves a Disease State, she or he will pick a new state from among those whose transitions are labelled with the person's treatment id, with
Planned Implementation of Disease Transmission
A transmission rate function returns the (baseline) probability of a person's becoming infected per minute of contact as a function of his/her disease transmission type and the type of an infectious person at the same location. That is, if exactly one susceptible of transmission type j and one infectious person transmission type k have been in a work location for one minute, the base probability that the susceptible has become infected is given by ρwork(j,k). The susceptible or infectious "person" may in fact be a location. Note that the transmission rate function need not be symmetric between susceptible and infective, and that it may be activity specific.
Planned Adjustments to Transmission Rates
The reason the probability returned by the transmission rate function is called a "baseline" is that it is further adjusted by duration of contact, number of people in the location, infectivity, and susceptibility.
Duration of Contact
If more or less time than one minute has passed, the probability is adjusted as for a Poisson process, using the survival rate and assuming the probability of infection in each time interval is independent. Thus if the base probability for infection per minute is p, the probability in t time units is 1 - (1-p)t.
Number of People Present
If more than one infective is present, the probability is scaled under the assumption that each infective spreads disease independently. Thus if there are Ni infectives of transmission type i, with probability of transmission pi, the overall probability of transmission in time t will be 1 - exp{t Σi Ni ln(1-pi)}. If M susceptibles are present, we divide the probability of transmission by the scale factor Mα, where α is a user specified scale factor. Each susceptible present undergoes a Bernoulli trial with the probability relevant to that person.
Infectivity and Susceptibility
If the infective has infectivity r, and the susceptible has susceptibility s, the base transmission probability is adjusted to be srρwork(j,k). The user should ensure that all possible resulting probabilities are less than unity. Taking into account the different levels of infectivity associated with each Disease State, if there are nk,r infectious people of type k with infectivity r, then the probability of infecting a single susceptible of type j in time t would be
p(t) = 1 - exp [t Σtypes k Σinfectivity r nk,r ln(1 - rρwork(j,k)j)].
Total probability of transmission
Putting everything together, the probability of infecting a person of transmission type j with susceptibility s in a location with activity type a with M susceptibles and nk,l infectious people of type k with infectivity r during a time t, subject to user specified scaling in susceptibles α, is:
pj,s(t) = {1 - exp [t Σtypes k Σinfectivity r nk,r (1 - rs ρ a(j,k)]}/Mα
Planned Disease Manifestation Constraints
There is a single consistency constraint on allowed values of attributes for a Disease State: non-zero incapacitation implies non-zero prodrome or symptoms. In particular, the following constraints are NOT imposed:
-
1.
infectious => symptomatic or prodromal
-
2.
dead => uninfectious (corpses can be hazardous)
In addition, the transition probabilities for each state must sum to unity by Treatment Id.
Planned Implementation of Behavioural Thresholds
Some actions taken at run time during the simulation depend on thresholds set by the user. For example, when a person becomes incapacitated, he or she will skip some normal activities. Which activities are skipped depends on the value of the person's incapacitation versus user specified thresholds. Similarly, symptomatic people may be mis-diagnosed if their level of symptoms is not above a user specified threshold. Also, symptomatic people may seek over-the-counter remedies or emergency care as the level of their symptoms rises. The user may specify a threshold value for incapacitated for staying home from any of the defined activity types. Furthermore, the user may specify any of the following thresholds for the symptomatic and prodrome attributes:
-
seek over-the-counter remedies
-
seek treatment at hospital/clinic
-
be readily diagnosed by trained physician, lab test, etc.
-
be readily diagnosed by casual observer (or contact tracer)
The user may specify two sets of thresholds – when more than a user specified number of people have been diagnosed with the disease the second set of thresholds will be used. This allows for the increased likelihood of correct diagnosis when the disease is known to be present in the community.
Planned Implementation of Prophylaxis and Treatment
Prophylaxis (before infection) is modelled by changing the person's susceptibility. The user must specify a distribution of susceptibilities to use. As usual, this distribution may be conditioned on people's demographics. The variability in susceptibility post-prophylaxis allows one to model variable efficacy.
During the course of the simulation, an individual may seek treatment as described above. Availability of treatment is constrained by the simulation based on available resources (in an as-yet-to-be-determined way) and on level of symptoms (also to be determined). The simulation will determine whether each individual seeking treatment receives it, and also what kind of treatment is given. Examples of possible treatments might include:
-
over-the-counter drugs
-
anti-virals
-
vaccinations
-
antibiotics
-
ventilators
-
hospitalization
-
morgue
The effect of treatment (after infection) is specified by the user in the Disease Manifestation Model. Each state transition may be labelled with a set of Treatment Ids. If it is not labelled, the transition is available to any individual. A labelled transition is only available to individuals who have received treatment at one of the ids included in the set.
Rights and permissions
About this article
Cite this article
Eubank, S., Guclu, H., Anil Kumar, V. et al. Modelling disease outbreaks in realistic urban social networks. Nature 429, 180–184 (2004). https://doi.org/10.1038/nature02541
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature02541
This article is cited by
-
Recent achievements and conceptual challenges for urban digital twins
Nature Computational Science (2024)
-
Central node identification via weighted kernel density estimation
Data Mining and Knowledge Discovery (2024)
-
Measuring unequal distribution of pandemic severity across census years, variants of concern and interventions
Population Health Metrics (2023)
-
Evaluation of COVID-19 intervention policies in South Korea using the stochastic individual-based model
Scientific Reports (2023)
-
A time evolving online social network generation algorithm
Scientific Reports (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.