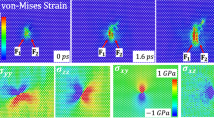
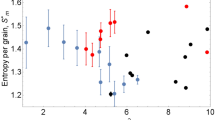
Abstract
Martensitic transformations are diffusionless, solid-to-solid phase transitions, and have been observed in metals, alloys, ceramics and proteins1,2. They are characterized by a rapid change of crystal structure, accompanied by the development of a rich microstructure. Martensitic transformations can be irreversible, as seen in steels upon quenching1, or they can be reversible, such as those observed in shape-memory alloys3,4. In the latter case, the microstructures formed on cooling are easily manipulated by loads and disappear upon reheating. Here, using mathematical theory and numerical simulation, we explain these sharp differences in behaviour on the basis of the change in crystal symmetry during the transition. We find that a necessary condition for reversibility is that the symmetry groups of the parent and product phases be included in a common finite symmetry group. In these cases, the energy barrier to lattice-invariant shear is generically higher than that pertaining to the phase change and, consequently, transformations of this type can occur with virtually no plasticity. Irreversibility is inevitable in all other martensitic transformations, where the energy barrier to plastic deformation (via lattice-invariant shears, as in twinning or slip) is no higher than the barrier to the phase change itself. Various experimental observations confirm the importance of the symmetry of the stable states in determining the macroscopic reversibility of martensitic transformations.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Olson, G. B. & Owen, W. (eds) Martensite (ASM International, Materials Park, OH, 1992)
Salje, E. K. H. Phase Transitions in Ferroelastic and Co-elastic Crystals (Cambridge Univ. Press, Cambridge, 1993)
Otsuka, K. & Wayman, C. M. Shape Memory Materials (Cambridge Univ. Press, Cambridge, 1998)
Barrett, C. S. & Massalski, T. B. Structure of Metals 3rd edn (Pergamon, Oxford, 1987)
Bocanegra-Bernal, M. H. & De la Torre, S. D. Phase transitions in zirconium dioxide and related materials for high performance engineering ceramics. J. Mater. Sci. 37, 4947–4971 (2002)
Olson, G. B. & Hartman, H. Martensite and life—displacive transformations as biological processes. J. Physique 43(C4), 855–865 (1982)
James, R. D. & Wuttig, M. Magnetostriction of martensite. Phil. Mag. A 77, 1273–1299 (1998)
Sozinov, A., Likhachev, A. A., Lanska, N. & Ullakko, K. Giant magnetic-field-induced strain in NiMnGa seven-layered martensitic phase. Appl. Phys. Lett. 80, 1746–1748 (2002)
Shu, Y. C. & Bhattacharya, K. Domain patterns and macroscopic behaviour of ferroelectric materials. Phil. Mag. B 81, 2021–2054 (2001)
de Gennes, P.-G. & Okumura, K. Phase transitions of nematic rubbers. Europhys. Lett. 63, 76–82 (2003)
Bhattacharya, K. Microstructure of Martensite: Why it Forms and How it Gives Rise to the Shape-Memory Effect (Oxford Univ. Press, Oxford, 2003)
Ericksen, J. L. Weak martensitic transformations in Bravais lattices. Arch. Ration. Mech. Anal. 107, 23–36 (1989)
Tolédano, P. & Dmitriev, V. Reconstructive Phase Transitions (World Scientific, Singapore, 1996)
Maki, T. & Tamura, I. in Proc. Int. Conf. on Martensitic Transformations 963–970 (The Japan Institute of Metals, Nara, 1986)
Barker, L. M. & Hollenbach, R. E. Shock wave study of the α↔ɛ phase transition in iron. J. Appl. Phys. 45, 4872–4887 (1974)
Kadau, K., Germann, T. C., Lomdahl, P. S. & Holian, B. L. Microscopic view of structural phase transitions induced by shock waves. Science 296, 1681–1684 (2002)
Liu, Y. et al. Thermomechanical behaviour of fcc↔hcp martensitic transformation in CoNi. J. Alloys Compd. (in the press)
Matsumoto, S., Sato, A. & Mori, T. Formation of h.c.p. and f.c.c. twins in an Fe-Mn-Cr-Si-Ni alloy. Acta Metall. Mater. 42, 1207–1213 (1994)
Yang, J. H. & Wayman, C. M. On secondary variants formed at intersections of ɛ martensite variants. Acta Metall. Mater. 40, 2011–2023 (1992)
Lee, H. H. et al. Orientational proliferation and successive twinning from thermoreversible hexagonal-body-centered cubic transitions. Macromolecules 35, 785–794 (2002)
Otsuka, K. & Shimizu, K. On the crystallographic reversibility of martensitic transformations. Scripta Met. 11, 757–760 (1977)
Schwarzenberger, R. L. E. Classification of crystal lattices. Proc. Camb. Phil. Soc. 72, 325–349 (1972)
Pitteri, M. & Zanzotto, G. Continuum Models for Phase Transitions and Twinning in Crystals (Chapman & Hall/CRC, Boca Raton, 2002)
Ericksen, J. L. Some phase transitions in crystals. Arch. Ration. Mech. Anal. 73, 99–124 (1980)
Pitteri, M. Reconciliation of local and global symmetries of crystals. J. Elast. 14, 175–190 (1984)
Ball, J. M. & James, R. D. Proposed experimental tests of a theory of fine microstructure and the two-well problem. Phil. Trans. R. Soc. Lond. A 338, 389–450 (1992)
Fonseca, I. Variational methods for elastic crystals. Arch. Ration. Mech. Anal. 97, 189–220 (1987)
Hull, D. & Bacon, D. J. Introduction to Dislocations 3rd edn (Pergamon, Oxford, 1984)
Conti, S. & Zanzotto, G. A variational model for reconstructive phase transformations in crystals, and their relation to dislocations and plasticity. Arch. Ration. Mech. Anal. (in the press)
Hua, L. K. & Reiner, I. On the generators of the symplectic modular group. Trans. Am. Math. Soc. 65, 415–426 (1949)
Acknowledgements
This work was largely carried out when J.Z. held a position at the California Institute of Technology. The work of S.C. and J.Z. was partially supported by the Deutsche Forschungsgemeinschaft. G.Z. acknowledges the partial support of the Italian MIUR (CoFin Modelli Matematici per i Materiali). S.C. and G.Z. acknowledge the partial support of the IV Framework Programme of the EU. K.B. and J.Z. acknowledge the partial financial support of the US Air Force Office of Scientific Research and the US Office of Naval Research. All authors contributed equally to this work.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing financial interests.
Rights and permissions
About this article
Cite this article
Bhattacharya, K., Conti, S., Zanzotto, G. et al. Crystal symmetry and the reversibility of martensitic transformations. Nature 428, 55–59 (2004). https://doi.org/10.1038/nature02378
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature02378
This article is cited by
-
Elucidating the pressure-induced enhancement of ionic conductivity in sodium closo-hydroborate electrolytes for all-solid-state batteries
Journal of Materials Science (2023)
-
Ericksen-Landau Modular Strain Energies for Reconstructive Phase Transformations in 2D Crystals
Journal of Elasticity (2023)
-
Atomistic mechanism of phase transformation between topologically close-packed complex intermetallics
Nature Communications (2022)
-
Fatigue Properties of Nickel Titanium and their Improvement Using Low-Energy High-Current Electron Beams
Russian Physics Journal (2021)
-
Unraveling Frequency Effects in Shape Memory Alloys: NiTi and FeMnAlNi
Shape Memory and Superelasticity (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.