Abstract
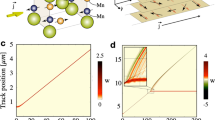
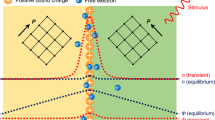
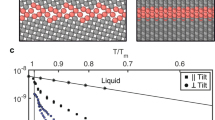
The discrete nature of crystal lattices plays a role in virtually every material property. But it is only when the size of entities hosted by a crystal becomes comparable to the lattice period—as occurs for dislocations1,2,3, vortices in superconductors4,5,6 and domain walls7,8,9—that this discreteness is manifest explicitly. The associated phenomena are usually described in terms of a background Peierls ‘atomic washboard’ energy potential, which was first introduced for the case of dislocation motion1,2 in the 1940s. This concept has subsequently been invoked in many situations to describe certain features in the bulk behaviour of materials, but has to date eluded direct detection and experimental scrutiny at a microscopic level. Here we report observations of the motion of a single magnetic domain wall at the scale of the individual peaks and troughs of the atomic energy landscape. Our experiments reveal that domain walls can become trapped between crystalline planes, and that they propagate by distinct jumps that match the lattice periodicity. The jumps between valleys are found to involve unusual dynamics that shed light on the microscopic processes underlying domain-wall propagation. Such observations offer a means for probing experimentally the physics of topological defects in discrete lattices—a field rich in phenomena that have been subject to extensive theoretical study10,11,12.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Peierls, R. E. The size of a dislocation. Proc. Phys. Soc. 52, 34–37 (1940)
Nabarro, F. R. N. Dislocations in a simple cubic lattice. Proc. Phys. Soc. 59, 256–272 (1947)
Kolar, H. R., Spence, J. C. H. & Alexander, H. Observation of moving dislocation kinks and unpinning. Phys. Rev. Lett. 77, 4031–4034 (1996)
Ivlev, B. I. & Kopnin, N. B. Flux creep and flux pinning in layered high-temperature superconductors. Phys. Rev. Lett. 64, 1828–1830 (1990)
Oussena, M., deGroot, P. A. J., Gagnon, R. & Taillefer, L. Lock-in oscillations in magnetic hysteresis curves of YBa2Cu3O7-x single crystals. Phys. Rev. Lett. 72, 3606–3609 (1994)
Kleiner, R., Steinmeyer, F., Kunkel, G. & Müller, P. Intrinsic Josephson effects in Bi2Sr2CaCu2O8 single crystals. Phys. Rev. Lett. 68, 2394–2397 (1992)
Barbara, B. Propriétés des parois étroites dans les substances ferromagnétiques à forte anisotropie. J. Phys 34, 1039–1046 (1973)
van den Broek, J. J. & Zijlstra, H. Calculation of intrinsic coercivity of magnetic domain walls in perfect crystals. IEEE Trans. Magn. 7, 226–230 (1971)
Egami, T. & Graham, C. D. Jr Domain walls in ferromagnetic Dy and Tb. J. Appl. Phys. 42, 1299–1300 (1971)
Aubry, S. Devils staircase and order without periodicity in classical condensed matter. J. Phys. 44, 147–162 (1983)
Braun, O. M. & Kivshar, Y. S. Nonlinear dynamics of the Frenkel-Kontorova model. Phys. Rep. 306, 2–108 (1998)
Bishop, A. R. & Lewis, W. F. A theory of intrinsic coercivity in narrow domain wall materials. J. Phys. C 12, 3811–3825 (1979)
Hilzinger, H. R. & Kronmüller, H. Spin configuration and intrinsic coercive field of narrow domain walls in Co5R-compounds. Phys. Status Solidi 54, 593–604 (1972)
Egami, T. Theory of intrinsic magnetic after-effect. Phys. Status Solidi 19, 747–758 (1973)
Arnaudas, J. I., del Moral, A. & Abell, J. S. Intrinsic coercive field in pseudobinary cubic intermetallic compounds. J. Magn. Magn. Mater. 61, 370–380 (1986)
Musbniskov, N. V., Andreev, A. V., Korolyov, A. V. & Shiokawa, Y. Magnetic viscosity in a UPtAl single crystal. J. Alloys Comp. 305, 188–193 (2002)
Geim, A. K. et al. Ballistic Hall micromagnetometry. Appl. Phys. Lett. 71, 2379–2381 (1997)
Geim, A. K. et al. Phase transitions in individual sub-micrometre superconductors. Nature 390, 259–262 (1997)
Pisarev, R. V. et al. Optical second-harmonic generation in magnetic garnet thin films. J. Phys. 5, 8621–8628 (1993)
Pavlov, V. V., Pisarev, R. V., Kirilyuk, A. & Rasing, T. Observation of a transversal nonlinear magneto-optical effect in thin magnetic garnet films. Phys. Rev. Lett. 78, 2004–2007 (1997)
Novoselov, K. S., Geim, A. K., van der Berg, D., Dubonos, S. V. & Maan, J. C. Domain wall propagation on nanometer scale: coercivity of a single pinning center. IEEE Trans. Magn. 38, 2583–2585 (2002)
Peeters, F. M. & Li, X. Q. Hall magnetometer in the ballistic regime. Appl. Phys. Lett. 72, 572–574 (1998)
Kent, A. D., von Molnar, S., Gider, S. & Awschalom, D. D. Properties and measurement of scanning tunneling microscope fabricated ferromagnetic particle arrays. J. Appl. Phys. 76, 6656–6660 (1994)
Li, Y. Q. et al. Hall magnetometry on a single iron nanoparticle. Appl. Phys. Lett. 80, 4644–4646 (2002)
Hengstmann, T. M., Grundler, D., Heyn, C. & Heitmann, D. Stray-field investigation on permalloy nanodisks. J. Appl. Phys. 90, 6542–6544 (2001)
Schuh, D., Biberger, J., Bauer, A., Breuer, W. & Weiss, D. Hall-magnetometry on ferromagnetic dots and dot arrays. IEEE Trans. Magn. 37, 2091–2093 (2001)
Vergne, R., Cotillard, J. C. & Porteseil, J. L. Some statistical aspects of magnetization processes in ferromagnetic bodies—motion of a single 180-degrees Bloch wall in an imperfect crystalline medium. Rev. Phys. Appl. 16, 449–476 (1981)
Wunderlich, J. et al. Influence of geometry on domain wall propagation in a mesoscopic wire. IEEE Trans. Magn. 37, 2104–2107 (2001)
Kim, D. H., Choe, S. B. & Shin, S. C. Direct observation of Barkhausen avalanche in Co thin films. Phys. Rev. Lett. 90, 087203 (2003)
Magnus, K. Vibrations (Blackie & Son, London, 1965)
Acheson, D. From Calculus to Chaos (Oxford Univ. Press, Oxford, 1997)
Acknowledgements
This research was supported by the EPSRC (UK). We thank S. Gillott and M. Sellers for technical assistance and J. Steeds for advice on dislocation motion. S.V.D. also acknowledges support from Russian Ministry of Science and Technology.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing financial interests.
Rights and permissions
About this article
Cite this article
Novoselov, K., Geim, A., Dubonos, S. et al. Subatomic movements of a domain wall in the Peierls potential. Nature 426, 812–816 (2003). https://doi.org/10.1038/nature02180
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature02180
This article is cited by
-
The Quantum Hall Effect and Von Klitzing Constant
Measurement Techniques (2021)
-
Micromagnetometry of two-dimensional ferromagnets
Nature Electronics (2019)
-
Energy landscape scheme for an intuitive understanding of complex domain dynamics in ferroelectric thin films
Scientific Reports (2015)
-
Nonlinear spin excitations in chiral magnetic solids
Russian Chemical Bulletin (2014)
-
Dynamic control of magnetic nanowires by light-induced domain-wall kickoffs
Nature Materials (2013)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.