Abstract
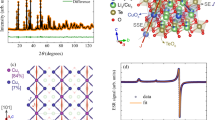
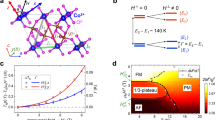
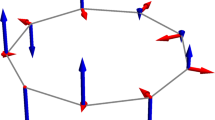
Frustrated systems are ubiquitous1,2,3, and they are interesting because their behaviour is difficult to predict; frustration can lead to macroscopic degeneracies and qualitatively new states of matter. Magnetic systems offer good examples in the form of spin lattices, where all interactions between spins cannot be simultaneously satisfied4. Here we report how unusual composite spin degrees of freedom can emerge from frustrated magnetic interactions in the cubic spinel ZnCr2O4. Upon cooling, groups of six spins self-organize into weakly interacting antiferromagnetic loops, whose directors—the unique direction along which the spins are aligned, parallel or antiparallel—govern all low-temperature dynamics. The experimental evidence comes from a measurement of the magnetic form factor by inelastic neutron scattering; the data show that neutrons scatter from hexagonal spin clusters rather than individual spins. The hexagon directors are, to a first approximation, decoupled from each other, and hence their reorientations embody the long-sought local zero energy modes for the pyrochlore lattice.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Debenedetti, P. G. & Stillinger, F. H. Supercooled liquids and the glass transition. Nature 410, 259–267 (2001)
Wolynes, P. G. & Eaton, W. A. The physics of protein folding. Phys. World 12, 39–44 (1999)
Bramwell, S. T. & Gingras, M. J. P. Spin ice state in frustrated magnetic pyrochlore materials. Science 294, 1495–1501 (2001)
Ramirez, A. P. in Handbook on Magnetic Materials (ed. Busch, K. J. H.) Vol. 13, 423–520 (Elsevier Science, Amsterdam, 2001)
Moessner, R. & Chalker, J. T. Properties of a classical spin liquid: the Heisenberg pyrochlore antiferromagnet. Phys. Rev. Lett. 80, 2929–2932 (1998)
Canals, B. & Lacroix, C. Pyrochlore antiferromagnet: a three-dimensional quantum spin liquid. Phys. Rev. Lett. 80, 2933–2936 (1998)
Stormer, H. L., Tsui, D. C. & Gossard, A. C. The fractional quantum Hall effect. Rev. Mod. Phys. 71, S298–S305 (1999)
Laughlin, R. B. & Pines, D. The theory of everything. Proc. Natl Acad. Sci. USA 97, 28–31 (2000)
Lovesey, S. W. Theory of Thermal Neutron Scattering from Condensed Matter (Clarendon, Oxford, 1984)
Birgeneau, R. J. et al. Instantaneous spin correlations in La2CuO4 . Phys. Rev. B 59, 13788–13794 (1999)
Lee, S.-H. et al. Spin-glass and non-spin-glass features of a geometrically frustrated magnet. Europhys. Lett. 35, 127–132 (1996)
Moessner, R. & Chalker, J. T. Low-temperature properties of classical, geometrically frustrated antiferromagnets. Phys. Rev. B 58, 12049–12062 (1998)
Lee, S.-H., Broholm, C., Kim, T. H., Ratcliff, W. & Cheong, S-W. Local spin resonance and spin-Peierls-like phase transition in a geometrically frustrated antiferromagnet. Phys. Rev. Lett. 84, 3718–3721 (2000)
Moessner, R. & Berlinsky, A. J. Magnetic susceptibility of diluted pyrochlore and SrCr9-9xGa3+9xO19 . Phys. Rev. Lett. 83, 3293–3296 (1999)
Garcia-Adeva, A. J. & Huber, D. L. Quantum tetrahedral mean-field theory of the pyrochlore lattice. Can. J. Phys. 79, 1359–1364 (2001)
Mekata, M. & Yamada, Y. Magnetic-ordering process in SrCr9(Ga-In)3O19 . Can. J. Phys. 79, 1421–1426 (2001)
Uemura, Y. J. et al. Spin fluctuations in frustrated kagomé lattice system SrCr8Ga4O19 studied by muon spin relaxation. Phys. Rev. Lett. 73, 3306–3309 (1994)
Ramirez, A. P., Espinosa, G. P. & Cooper, A. S. Elementary excitations in a diluted antiferromagnetic kagomé lattice. Phys. Rev. B 45, 2505–2508 (1992)
Broholm, C., Aeppli, G., Espinosa, G. P. & Cooper, A. S. Antiferromagnetic fluctuations and short range order in a kagomé lattice. Phys. Rev. Lett. 65, 3173–3716 (1990)
Pande, V. S., Grosberg, A. Yu. & Tanaka, T. Heteropolymer freezing and design: Towards physical models of protein folding. Rev. Mod. Phys. 72, 259–314 (2000)
Acknowledgements
We thank O. Tchernyshyov, R. Moessner, S. L. Sondhi, A. B. Harris, G. Aeppli, N. Read and D. Weitz for discussions, J. J. Rush, A. P. Ramirez and P. M. Gehring for critical reading of the manuscript, and Z. Huang for assistance in making figures. This work was partially supported by the NSF and the BSF.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing financial interests.
Rights and permissions
About this article
Cite this article
Lee, SH., Broholm, C., Ratcliff, W. et al. Emergent excitations in a geometrically frustrated magnet. Nature 418, 856–858 (2002). https://doi.org/10.1038/nature00964
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature00964
This article is cited by
-
Mössbauer study of A-site ordered spinel LiFeCr4O8
Interactions (2024)
-
A self-adaptive first-principles approach for magnetic excited states
Quantum Frontiers (2023)
-
Coexisting Z-type charge and bond order in metallic NaRu2O4
Communications Materials (2022)
-
Dichotomy in temporal and thermal spin correlations observed in the breathing pyrochlore LiGa1−xInxCr4O8
npj Quantum Materials (2021)
-
Dimensional reduction by geometrical frustration in a cubic antiferromagnet composed of tetrahedral clusters
Nature Communications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.