Abstract
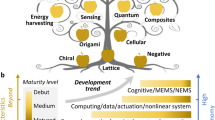
Mechanical metamaterials exhibit properties and functionalities that cannot be realized in conventional materials. Originally, the field focused on achieving unusual (zero or negative) values for familiar mechanical parameters, such as density, Poisson's ratio or compressibility, but more recently, new classes of metamaterials — including shape-morphing, topological and nonlinear metamaterials — have emerged. These materials exhibit exotic functionalities, such as pattern and shape transformations in response to mechanical forces, unidirectional guiding of motion and waves, and reprogrammable stiffness or dissipation. In this Review, we identify the design principles leading to these properties and discuss, in particular, linear and mechanism-based metamaterials (such as origami-based and kirigami-based metamaterials), metamaterials harnessing instabilities and frustration, and topological metamaterials. We conclude by outlining future challenges for the design, creation and conceptualization of advanced mechanical metamaterials.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout







Similar content being viewed by others
References
Soukoulis, C. & Wegener, M. Past achievements and future challenges in the development of three-dimensional photonic metamaterials. Nat. Photonics 5, 523–530 (2011).
Cummer, S. A., Christensen, J. & Alù, A. Controlling sound with acoustic metamaterials. Nat. Rev. Mater. 1, 16001 (2016).
Schittny, R., Kadic, M., Guenneau, S. & Wegener, M. Experiments on transformation thermodynamics: molding the flow of heat. Phys. Rev. Lett. 110, 195901 (2013).
Pendry, J. B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 85, 3966–3969 (2000).
Kadic, M., Bückmann, T., Schittny, R. & Wegener, M. Metamaterials beyond electromagnetism. Rep. Prog. Phys. 76, 126501 (2013).
Christensen, J., Kadic, M., Kraft, O. & Wegener, M. Vibrant times for mechanical metamaterials. MRS Commun. 5, 453–462 (2015).
Lakes, R. Foam structures with a negative Poisson's ratio. Science 235, 1038–1040 (1987).
Lakes, R. Deformation mechanisms of negative Poisson's ratio materials: structural aspects. J. Mater. Sci. 26, 2287–2292 (1991).
Milton, G. Composite materials with poisson's ratios close to — 1. J. Mech. Phys. Solids 40, 1105–1137 (1992).
Milton, G. W. & Cherkaev, A. V. Which elasticity tensors are realizable? J. Eng. Mater. Technol. 117, 483–493 (1995).
Kadic, M., Bückmann, T., Stenger, N., Thiel, M. & Wegener, M. On the practicability of pentamode mechanical metamaterials. Appl. Phys. Lett. 100, 191901 (2012).
Nicolaou, Z. G. & Motter, A. E. Mechanical metamaterials with negative compressibility transitions. Nat. Mater. 11, 608–613 (2012).
Bückmann, T., Thiel, M., Kadic, M., Schittny, R. & Wegener, M. An elasto-mechanical unfeelability cloak made of pentamode metamaterials. Nat. Commun. 5, 4130 (2014).
Schenk, M. & Guest, S. D. Geometry of miura-folded metamaterials. Proc. Natl Acad. Sci. USA 110, 3276–3281 (2013).
Yasuda, H. & Yang, J. Reentrant origami-based metamaterials with negative Poisson's ratio and bistability. Phys. Rev. Lett. 114, 185502 (2015).
Gatt, R. et al. Hierarchical auxetic mechanical metamaterials. Sci. Rep. 5, 8395 (2015).
Babaee, S. et al. 3D soft metamaterials with negative Poisson's ratio. Adv. Mater. 25, 5044–5049 (2013).
Liu, J. et al. Harnessing buckling to design architected materials that exhibit effective negative swelling. Adv. Mater. 28, 6619–6624 (2016).
Miura, K. Method of packaging and deployment of large membranes in space. Inst. Space Astronaut. Sci. Rep. 618, 1–9 (1985).
Hawkes, E. et al. Programmable matter by folding. Proc. Natl Acad. Sci. USA 107, 12441–12445 (2010).
Tachi, T. & Miura, K. Rigid-foldable cylinders and cells. J. Int. Shell Spat. Struct. 53, 217–226 (2012).
Wei, Z. Y., Guo, Z. V., Dudte, L., Liang, H. Y. & Mahadevan, L. Geometric mechanics of periodic pleated origami. Phys. Rev. Lett. 110, 215501 (2013).
Lv, C., Krishnaraju, D., Konjevod, G., Yu, H. & Jiang, H. Origami based mechanical metamaterials. Sci. Rep. 4, 5979 (2014).
Lechenault, F., Thiria, B. & Adda-Bedia, M. Mechanical response of a creased sheet. Phys. Rev. Lett. 112, 244301 (2014).
Cheung, K. C., Tachi, T., Calisch, S. & Miura, K. Origami interleaved tube cellular materials. Smart Mater. Struct. 23, 094012 (2014).
Cho, Y. et al. Engineering the shape and structure of materials by fractal cut. Proc. Natl Acad. Sci. USA 111, 17390 (2014).
Waitukaitis, S., Menaut, R., Chen, B. G. & van Hecke, M. Origami multistability: from single vertices to metasheets. Phys. Rev. Lett. 114, 055503 (2015).
Shyu, T. et al. A kirigami approach to engineering elasticity in nanocomposites through patterned defects. Nat. Mater. 14, 785–789 (2015).
Filipov, E. T., Tachi, T. & Paulino, G. H. Origami tubes assembled into stiff, yet reconfigurable structures and metamaterials. Proc. Natl Acad. Sci. USA 112, 12321–12326 (2015).
Coulais, C., Teomy, E., de Reus, K., Shokef, Y. & van Hecke, M. Combinatorial design of textured mechanical metamaterials. Nature 535, 529–532 (2016).
Isobe, M. & Okumura, K. Initial rigid response and softening transition of highly stretchable kirigami sheet materials. Sci. Rep. 6, 24758 (2016).
Dudte, L., Vouga, E., Tachi, T. & Mahadevan, L. Programming curvature using origami tessellations. Nat. Mater. 15, 583–588 (2016).
Haghpanah, B. et al. Multistable shape-reconfigurable architected materials. Adv. Mater. 28, 7915–7920 (2016).
Overvelde, J. T. et al. A three-dimensional actuated origami-inspired transformable metamaterial with multiple degrees of freedom. Nat. Commun. 7, 10929 (2016).
Overvelde, J. T., Weaver, J., Hoberman, C. & Bertoldi, K. Rational design of reconfigurable prismatic architected materials. Nature 541, 347–352 (2017).
Prodan, E. & Prodan, C. Topological phonon modes and their role in dynamic instability of microtubules. Phys. Rev. Lett. 103, 248101 (2009).
Kane, C. L. & Lubensky, T. C. Topological boundary modes in isostatic lattices. Nat. Phys. 10, 39–45 (2014).
Chen, B. G., Upadhyaya, N. & Vitelli, V. Nonlinear conduction via solitons in a topological mechanical insulator. Proc. Natl Acad. Sci. USA 111, 13004–13009 (2014).
Vitelli, V., Upadhyaya, N. & Chen, B. G. Topological mechanisms as classical spinor fields. Preprint at http://arxiv.org/abs/1407.2890v2 (2014).
Paulose, J., Chen, B. G. & Vitelli, V. Topological modes bound to dislocations in mechanical metamaterials. Nat. Phys. 11, 153–156 (2015).
Paulose, J., Meeussen, A. S. & Vitelli, V. Selective buckling via states of self-stress in topological metamaterials. Proc. Natl Acad. Sci. USA 112, 7639–7644 (2015).
Nash, L. M. et al. Topological mechanics of gyroscopic metamaterials. Proc. Natl Acad. Sci. USA 112, 14495–14500 (2015).
Khanikaev, A. B., Fleury, R. & Mousavi, S. H. & Alù, A. Topologically robust sound propagation in an angular-momentum-biased graphene-like resonator lattice. Nat. Commun. 6, 8260 (2015).
Susstrunk, R. & Huber, S. D. Observation of phononic helical edge states in a mechanical topological insulator. Science 349, 47–50 (2015).
Meeussen, A. S., Paulose, J. & Vitelli, V. Geared topological metamaterials with tunable mechanical stability. Phys. Rev. X 6, 041029 (2016).
Rocklin, D. Z., Chen, B. G., Falk, M., Vitelli, V. & Lubensky, T. C. Mechanical Weyl modes in topological Maxwell lattices. Phys. Rev. Lett. 116, 135503 (2016).
Kariyado, T. & Hatsugai, Y. Manipulation of Dirac cones in mechanical graphene. Sci. Rep. 5, 18107 (2015).
Chen, B. G. et al. Topological mechanics of origami and kirigami. Phys. Rev. Lett. 116, 135501 (2016).
Mousavi, S. H., Khanikaev, A. B. & Wang, Z. Topologically protected elastic waves in phononic metamaterials. Nat. Commun. 6, 8682 (2015).
Xiao, M., Chen, W.-J., He, W.-Y. & Chan, C. T. Synthetic gauge flux and Weyl points in acoustic systems. Nat. Phys. 11, 920–924 (2015).
Rocklin, D. Z., Zhou, S., Sun, K. & Mao, X. Transformable topological mechanical metamaterials. Nat. Commun. 8, 14201 (2017).
Yang, Z. et al. Topological acoustics. Phys. Rev. Lett. 114, 1–4 (2015).
Süsstrunk, R. & Huber, S. D. Classification of topological phonons in linear mechanical metamaterials. Proc. Natl Acad. Sci. USA 113, E4767–E4775 (2016).
Deymier, P. A., Runge, K., Swinteck, N. & Muralidharan, K. Torsional topology and fermion-like behavior of elastic waves in phononic structures. Comptes Rendus Mécanique 343, 700–711 (2015).
Bi, R. & Wang, Z. Unidirectional transport in electronic and photonic Weyl materials by dirac mass engineering. Phys. Rev. B 92, 241109 (2015).
Berg, N., Joel, K., Koolyk, M. & Prodan, E. Topological phonon modes in filamentary structures. Phys. Rev. E 83, 021913 (2011).
Peano, V., Brendel, C., Schmidt, M. & Marquardt, F. Topological phases of sound and light. Phys. Rev. X 5, 031011 (2015).
Wang, Y.-T., Luan, P.-G. & Zhang, S. Coriolis force induced topological order for classical mechanical vibrations. New J. Phys. 17, 073031 (2015).
Wang, P., Lu, L. & Bertoldi, K. Topological phononic crystals with one-way elastic edge waves. Phys. Rev. Lett. 115, 104302 (2015).
Po, H. C., Bahri, Y. & Vishwanath, A. Phonon analog of topological nodal semimetals. Phys. Rev. B 93, 205158 (2016).
Coulais, C., Sounas, D. & Alù, A. Static non-reciprocity in mechanical metamaterials. Nature 542, 461–464 (2017).
Mullin, T., Deschanel, S., Bertoldi, K. & Boyce, M. C. Pattern transformation triggered by deformation. Phys. Rev. Lett. 99, 084301 (2007).
Bertoldi, K., Reis, P. M., Willshaw, S. & Mullin, T. Negative Poisson's ratio behavior induced by an elastic instability. Adv. Mater. 22, 361–366 (2010).
Shim, J., Perdigou, C., Chen, E., Bertoldi, K. & Reis, P. Buckling-induced encapsulation of structured elastic shells under pressure. Proc. Natl Acad. Sci. USA 109, 5978–5983 (2012).
Florijn, B., Coulais, C. & van Hecke, M. Programmable mechanical metamaterials. Phys. Rev. Lett. 113, 175503 (2014).
Coulais, C., Overvelde, J. T., Lubbers, L. A., Bertoldi, K. & van Hecke, M. Discontinuous buckling of wide beams and metabeams. Phys. Rev. Lett. 115, 044301 (2015).
Fargette, A., Neukirch, S. & Antkowiak, A. Elastocapillary snapping: capillarity induces snap-through instabilities in small elastic beams. Phys. Rev. Lett. 112, 137802 (2014).
Silverberg, J. L. et al. Using origami design principles to fold reprogrammable mechanical metamaterials. Science 345, 647–650 (2014).
Kang, S. H. et al. Complex ordered patterns in mechanical instability induced geometrically frustrated triangular cellular structures. Phys. Rev. Lett. 112, 098701 (2014).
Shan, S. et al. Multistable architected materials for trapping elastic strain energy. Adv. Mater. 27, 4296 (2015).
Silverberg, J. L. et al. Origami structures with a critical transition to bistability arising from hidden degrees of freedom. Nat. Mater. 14, 389–393 (2015).
Zhang, Y. et al. A mechanically driven form of kirigami as a route to 3D mesostructures in micro/nanomembranes. Proc. Natl Acad. Sci. USA 112, 11757–11764 (2015).
Raney, J. R. et al. Stable propagation of mechanical signals in soft media using stored elastic energy. Proc. Natl Acad. Sci. USA 113, 9722–9727 (2016).
Rafsanjani, A., Akbarzadeh, A. & Pasini, D. Snapping mechanical metamaterials under tension. Adv. Mater. 55, 5931–5935 (2007).
Alexander, S. Amorphous solids: their structure, lattice dynamics and elasticity. Phys. Rep. 296, 65–236 (1998).
van Hecke, M. Jamming of soft particles: geometry, mechanics, scaling and isostaticity. J. Phys. Condens. Matter 22, 033101 (2010).
Katgert, G., Tighe, B. P. & van Hecke, M. The jamming perspective on wet foams. Soft Matter 9, 9739–9746 (2013).
Jaeger, H. M., Nagel, S. R. & Behringer, R. P. Granular solids, liquids, and gases. Rev. Mod. Phys. 68, 1259 (2012).
Broedersz, C. P. & MacKintosh, F. C. Modeling semiflexible polymer networks. Rev. Mod. Phys. 86, 995 (2014).
Jacobs, D. J. & Thorpe, M. F. Generic rigidity percolation: the pebble game. Phys. Rev. Lett. 75, 4051–4054 (1995).
Wyart, M., Liang, H., Kabla, A. & Mahadevan, L. Elasticity of floppy and stiff random networks. Phys. Rev. Lett. 101, 215501 (2008).
Ellenbroek, W. G., Zeravcic, Z., van Saarloos, W. & van Hecke, M. Non-affine response: jammed packings versus spring networks. EPL 87, 34004 (2009).
Ellenbroek, W. G., Hagh, V. F., Kumar, A., Thorpe, M. F. & van Hecke, M. Rigidity loss in disordered systems: three scenarios. Phys. Rev. Lett. 114, 135501 (2015).
Goodrich, C. P., Liu, A. J. & Nagel, S. R. The principle of independent bond-level response: tuning by pruning to exploit disorder for global behavior. Phys. Rev. Lett. 114, 225501 (2015).
O’Rourke, J. How to Fold It: The Mathematics of Linkages, Origami and Polyhedra (Cambridge Univ. Press, 2011).
Grima, J. N. & Evans, K. E. Auxetic behavior from rotating squares. J. Mater. Sci. Lett. 19, 1563–1565(2000).
Overvelde, J. T., Shan, S. & Bertoldi, K. Compaction through buckling in 2D periodic, soft and porous structures: effect of pore shape. Adv. Mater. 24, 2337–2342 (2012).
Overvelde, J. T. & Bertoldi, K. Relating pore shape to the non-linear response of periodic elastomeric structures. J. Mech. Phys. Solids 64, 351–366 (2014).
Kuribayashi, K. et al. Self-deployable origami stent grafts as a biomedical application of Ni-rich TiNi shape memory alloy foil. Mater. Sci. Eng. A 419, 131–137 (2006).
Song, Z. et al. Origami lithium-ion batteries. Nat. Commun. 5, 3140 (2014).
Goldman, F. in Origami5: Fifth International Meeting of Origami Science, Mathematics, and Education (eds Wang-Iverson, P., Lang, R. J . & Yim, M. ) 99–110 (CRC Press, 2011).
Blees, K. et al. Graphene kirigami. Nature 524, 204–207 (2015).
Song, Z. et al. Kirigami-based stretchable lithium-ion batteries. Sci. Rep. 5, 10988 (2015).
Xu, L. et al. Kirigami nanocomposites as wide-angle diffraction gratings. ACS Nano 10, 6156–6162 (2016).
Rafsanjani, A. & Bertoldi, K. Buckling-induced kirigami. Phys. Rev. Lett. 118, 084301 (2017).
Lamoureux, A. et al. Dynamic kirigami structures for integrated solar tracking. Nat. Commun. 6, 8092 (2015).
Eidini, M. & Paulino, G. H. Unraveling metamaterial properties in zigzag-base folded sheets. Sci. Adv. 1, e1500224 (2015).
Sussman, D. et al. Algorithmic lattice kirigami: a route to pluripotent materials. Proc. Natl Acad. Sci. USA 112, 7449–7453 (2015).
Bückmann, T. et al. Tailored 3D mechanical metamaterials made by dip-in direct-laser-writing optical lithography. Adv. Mater. 24, 2710–2714 (2012).
Gibson, L. & Ashby, M. Cellular Solids: Structure and Properties 2 nd edn (Cambridge Univ. Press, 1999).
Wierzbicki, T. & Abramowicz, W. On the crushing mechanics of thin-walled structures. J. Appl. Mech. 50, 727–734 (1983).
Papka, S. & Kyriakides, S. Biaxial crushing of honeycombs: — part1: experiments. Int. J. Solids Struct. 36, 4367–4396 (1999).
Papka, S. & Kyriakides, S. In-plane biaxial crushing of honeycombs:— part II: analysis. Int. J. Solids Struct. 36, 4397–4423 (1999).
Wu, E. & Jiang, W. Axial crush of metallic honeycombs. Int. J. Impact Eng. 19, 439–456 (1997).
Hayes, A. M., Wang, A., Dempsey, B. M. & McDowell, D. L. Mechanics of linear cellular alloys. Mech. Mater. 36, 691–713 (2004).
Zhang, Y. et al. One-step nanoscale assembly of complex structures via harnessing of an elastic instability. Nano Lett. 8, 1192–1196 (2008).
Babaee, S., Shim, J., Weaver, J., Patel, N. & Bertoldi, K. 3D soft metamaterials with negative Poisson's ratio. Adv. Mater. 25, 5044–5049 (2013).
Bertoldi, K. & Boyce, M. C. Mechanically-triggered transformations of phononic band gaps in periodic elastomeric structures. Phys. Rev. B 77, 052105 (2008).
Wang, P., Casadei, F., Shan, S., Weaver, J. & Bertoldi, K. Harnessing buckling to design tunable locally resonant acoustic metamaterials. Phys. Rev. Lett. 113, 014301 (2014).
Shan, S. et al. Harnessing multiple folding mechanisms in soft periodic structures for tunable control of elastic waves. Adv. Funct. Mater. 24, 4935–4942 (2014).
Krishnan, D. & Johnson, H. Optical properties of two dimensional polymer photonic crystals after deformation induced pattern transformations. J. Mech. Phys. Solids 57, 1500–1513 (2009).
Li, J. et al. Switching periodic membranes via pattern transformation and shape memory effect. Soft Matter 8, 10322–10328 (2012).
Kang, S. et al. Buckling-induced reversible symmetry breaking and amplification of chirality using supported cellular structures. Adv. Mater. 25, 3380–3385 (2013).
Bazant, Z. P. & Cedolin, L. Stability of Structures: Elastic, Inelastic, Fracture, and Damage Theories (Oxford Univ. Press, 1991).
Pandey, A., Moulton, D., Vella, D. & Holmes, D. Dynamics of snapping beams and jumping poppers. EPL 105, 24001 (2014).
Restrepo, D., Mankame, N. D. & Zavattieri, P. D. Phase transforming cellular materials. EML 4, 52–60 (2015).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Lubensky, T. C., Kane, C. L., Mao, X., Souslov, A. & Sun, K. Phonons and elasticity in critically coordinated lattices. Rep. Prog. Phys. 78, 073901 (2015).
Zhou, Y., Chen, B. G., Upadhyaya, N. & Vitelli, V. Kink-antikink asymmetry and impurity interactions in topological mechanical chains. Phys. Rev. E 95, 022202 (2017).
Mitchell, N. P., Nash, L. M., Hexner, D., Turner, A. & Irvine, W. T. M. Amorphous gyroscopic topological metamaterials. Preprint at https://arxiv.org/abs/1612.09267 (2016).
Souslov, A., van Zuiden, B. C., Bartolo, D. & Vitelli, V. Topological sound in active-liquid metamaterials. Nat. Phys.http://dx.doi.org/10.1038/nphys4193 (2017).
Coulais, C., Kettenis, C. & van Hecke, M. A characteristic length scale causes anomalous size effects and boundary programmability in mechanical metamaterials. Nat. Phys.http://dx.doi.org/10.1038/nphys4269 (2017).
Lang, R. J. in Proc. 12 th Ann. Symp. Comp. Geo. (eds Whitesides, S. H. ) 98–105 (ACM, 1996).
Felton, S., Tolley, M., Demaine, E., Rus, D. & Wood, R. A method for building self-folding machines. Science 345, 644–646 (2014).
Zeravcic, Z., Manoharan, V. N. & Brenner, M. P. Size limits of self-assembled colloidal structures made using specific interactions. Proc. Natl Acad. Sci. USA 111, 15918–15923 (2014).
Miskin, M. Z. & Jaeger, H. M. Adapting granular materials through artificial evolution. Nat. Mater. 12, 326–331 (2013).
Acknowledgements
J.C. acknowledges support from the European Research Council (ERC) through the Starting Grant No. 714577 PHONOMETA and from the Ministerio de Economía, Industria y Competitividad (MINECO) through a Ramon y Cajal grant (Grant No. RYC-2015-17156). M.vH. acknowledges funding from the Netherlands Organisation for Scientific Research through Grant VICI No. NWO-680-47-609. V.V. acknowledges support from the University of Chicago Materials Research Science and Engineering Center, which is funded by the National Science Foundation through Grant No. DMR-1420709.
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the preparation of this manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Rights and permissions
About this article
Cite this article
Bertoldi, K., Vitelli, V., Christensen, J. et al. Flexible mechanical metamaterials. Nat Rev Mater 2, 17066 (2017). https://doi.org/10.1038/natrevmats.2017.66
Published:
DOI: https://doi.org/10.1038/natrevmats.2017.66
This article is cited by
-
Shell buckling for programmable metafluids
Nature (2024)
-
Static vector solitons in a topological mechanical lattice
Communications Physics (2024)
-
Perfect circular polarization of elastic waves in solid media
Nature Communications (2024)
-
Curvature tuning through defect-based 4D printing
Communications Materials (2024)
-
A quirky fluid that has robotic capabilities
Nature (2024)