Abstract
This review article examines digital microfluidic systems that manipulate droplets through surface anisotropy. These systems are categorized as surface tension driven or contact line driven. Surface tension driven systems include electrowetting on dielectric, Marangoni flow on microheater arrays, and chemical gradient surfaces, whereas contact line driven systems include anisotropic ratchet conveyors, nanostructured Parylene ratchets, and tilted pillar arrays. This article describes the operating principles and outlines the fabrication procedures for each system. We also present new equations that unify several previous models of contact line driven systems. The strengths and weaknesses of each system are compared, with a focus on their ability to perform the generation, switching, fusion, and fission of droplets. Finally, we discuss current and potential future applications of these systems.
Similar content being viewed by others
Introduction
Droplet microfluidics is an interdisciplinary field focused on the transport of fluids in small discrete volumes rather than through continuous flow. Like conventional microfluidics, droplet microfluidics arose from advances in microelectromechanical system (MEMS). Early droplet microfluidic systems generated micro- or nano-scale droplets of one liquid by applying a shear flow with a second immiscible liquid, essentially creating an emulsion (typically water in oil)1–3. The segmented flow of droplet microfluidics significantly reduces the volume and reactant quantity requirements compared to continuous flow systems, and it circumvents the issues of Taylor dispersion, solute–surface interactions and cross-contamination4–7. For these reasons, droplet microfluidic platforms are ideal for many biological and chemical applications, such as high throughput screening8–10, enzymatic and cell assays11–13, and combinatorial chemistry14–16. However, droplets in segmented flow systems are not individually addressed. More recently, an emerging area of microfluidics, described as “digital microfluidics” (DMF), has made it possible manipulate individual droplets without microchannels or encapsulating liquids6,7. Although current DMF systems operate with larger droplets at lower transport rates6,7, these systems have the potential to meet a broad range of applications and fulfill a unique niche in the field of microfluidics. Many DMF systems can control droplets through anisotropies on the underlying substrate; these systems will be the focus of this review.
DMF Systems
Each droplet on a DMF system can be thought of as a unit or “bit” of information, and DMF systems can manipulate droplets independently. This is a significant advantage over segmented flow systems that control droplets in series through the flow of an immiscible liquid in microchannels6,7. DMF systems covered in this review can continuously transport droplets by using surface anisotropy. This anisotropy can be actively created (e.g., by applying a voltage or shining a light source) or passive (e.g., by way of chemical gradients or surface texture). These anisotropies manipulate droplets either by modulating the surface tension or by asymmetrically guiding the contact line (“footprint”) of the droplet.
Surface tension driven DMFs
The term “surface tension driven” was first used by Lee et al.17 in 2002 to describe DMF devices that transport liquid droplets by creating surface tension gradients within the droplet. These gradients induce flow patterns that move the droplet along a substrate. DMF systems have implemented this principle by using electrical or thermal energy, as well as chemical gradient surfaces.
Electrowetting
Electrowetting on dielectric (EWOD) was the first DMF platform and is one of the best-developed methods of manipulating droplets7,18. EWOD controls droplets by using voltages applied at electrodes just below the substrate surface (Figure 1a). The applied voltage creates a charge at the interface between the droplet and the electrode. This charge causes a local reduction in surface tension (also referred to as interfacial energy) at the solid–liquid interface (γSL), which reduces the contact angle in this region17–19. The surface tension is unchanged in the area where no voltage is applied, and the contact angle is larger in this region. The effect of voltage on surface tension is described by Lippmann's equation (Equation (1))17–19, in which ε and d are the permittivity and thickness of the insulator between the electrodes and the droplet, respectively, and V is the applied voltage.
DMF systems transport droplets through surface anisotropy. These systems include (a) EWOD (adapted with permission from Ref 7 Copyright 2008 John Wiley & Sons), (b) microheater array (adapted with permission from Ref 20 Copyright 2003 IEEE), (c) chemical gradient (adapted with permission from Ref 21 Copyright 2006 American Chemical Society), (d) ARC (adapted with permission from Ref 22 Copyright 2012 John Wiley & Sons) with (e) schematic of operating principle, (f) nanostructured Parylene (adapted with permission from Ref 23 Copyright 2008 Elsevier) with (g) schematic of operating principle, and (h) TPA platforms (adapted with permission from Ref 24 Copyright 2014 John Wiley & Sons).
This local change in solid–liquid surface tension induces flow in the direction of lower surface tension, effectively wetting the surface where the voltage is applied. This wetting effect is described by a combination of Lippmann's and Young's Equations (Equation (2))17–19, where θ0 is the contact angle with no applied voltage, c is the capacitance per unit area of the electrode, and γLG is the surface tension at the liquid–gas interface.
This equation shows that the contact angle (θ) will decrease with increasing applied voltage (V). This makes the electrode surface more hydrophilic and “pulls” the droplet onto the surface over the electrode17–19.
EWOD devices are traditionally fabricated by patterning metal electrodes (typically gold or chromium) on a glass or quartz wafer, and coating the electrodes with a hydrophobic, dielectric material, such as Teflon17–19. A second wafer, typically etched or coated with a dielectric, is often placed on top to enclose the droplet17–19.
Optoelectrowetting (OEW) devices rely on the same principles of EWOD, but the voltage is applied by focusing light on a photoconductive material beneath the droplet. OEW devices were first fabricated by patterning a layer of indium-tin-oxide (ITO) on a transparent glass slide, and connecting ITO electrodes to the biasing lines with strips of amorphous silicon (a-Si:H)25. This layer is separated from the glass by a thin layer of silicon dioxide, and coated with Teflon, a hydrophobic dielectric material. A voltage is initially applied to the biasing lines, and illumination of the a-Si:H connection triggers the electrowetting effect at the ITO electrode25.
Microheater arrays
Microheater arrays transport droplets through thermocapillary forces (Figure 1b). Because surface tension is a function of temperature, applying a thermal gradient to a droplet creates a surface tension gradient within the droplet, which results in Marangoni flow26,27. The Marangoni flow opposes the viscous or “restoring” force caused by the surface that acts on the droplet, resulting in a net velocity (V). This relationship is described by Equation (3)26,27:
where V* is the characteristic velocity (liquid–gas surface tension, γLG, divided by viscosity), h0 is the height of the center of mass of the droplet, T is the prescribed temperature, and S, the spreading coefficient, is the relationship between solid–gas, γSG, solid–liquid, γSL, and liquid–gas surface tension (S = γSG – (γSL + γLG)) observed on the substrate surface. Interestingly, the spreading coefficient shows little response to temperature changes when S is small (dS/dT ≈ 0)26,27. In this case, the Marangoni flow dominates and the droplet moves in the direction of higher surface tension (i.e., towards the cold side) because dγLG/dT is negative26,27. Microheater arrays make use of this phenomenon with periodically placed resistive heaters that essentially “push” droplets towards a cooler region when the substrate is heated20.
Microheater arrays have been fabricated by patterning resistive heaters composed of titanium or chromium onto a rigid substrate (e.g., glass). Gold is used to form the leads to the heaters, and self-assembled monolayer patterns are used to prevent the droplets from spreading outside the path of resistive heaters20.
Chemical gradients
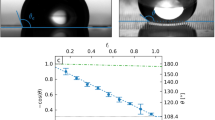
The surface tension at the solid–liquid interface of a droplet is related to the contact angle (Figure 1c) through Young's equation (Equation (4))28.
The contact angle of a liquid droplet measures wettability, which is determined by the chemical composition of a surface28. As a result of this relationship, a chemical gradient surface will cause the spreading coefficient (S = γSG – (γSL + γLG)) to vary spatially26. In this case, Marangoni flow is not present, so the droplet will move in the direction of lower surface tension (i.e., towards the hydrophilic region)26. This is similar to the effect described by Equation (3), but Equation (5) more accurately models the velocity of the droplet in this case26.
The log defines the limits of the flow region, where lmax is the macroscopic cutoff, lmin is a molecular size, and η is the viscosity of the droplet26. The velocity of the droplet is directly proportional to the surface tension gradient (described by the change in the spreading coefficient along the surface, dS/dx) and, by extension, the wettability gradient. This concept was first used to show that a chemical gradient could transport a droplet uphill29. However, the gradients used were static and could move droplets only a limited distance. Since then, droplets have been moved on wettability gradients created by selective exposure of photosensitive surfaces30.
Fabrication of a photosensitive surface for inducing wettability gradients was first performed by coating a glass substrate with macrocycle amphiphile (O-carboxymethylated calix[4]resorcinarine)30. More recently, photoreversible or “rewritable” photosensitive surfaces have been fabricated through layer-by-layer deposition of a polyelectrolyte (poly[allylamine hydrocholoride]) and SiO2 nanoparticles on negatively charged silicon wafers21, as well as by atomic layer deposition of zinc oxide films on glass and quartz wafers31. These systems can continuously drive droplet motion by maintaining surface energy gradients through active control of light beams.
Contact line driven DMFs
When vertical vibrations are applied to a droplet resting on a substrate, axisymmetric waves will form along the surface of the droplet32. Once they achieve sufficient amplitude, the vibrations cause the contact line (the perimeter of the droplet in contact with the substrate) to oscillate32. Each oscillation cycle is composed of two phases: an expansion phase and a contraction phase. A droplet oscillating on a homogeneous substrate enters the expansion phase when the contact line is at its smallest circumference. The contact line then advances in all directions throughout this phase. During the contraction phase, the contact line starts at its largest circumference and recedes until the next expansion phase begins. Contact line driven DMFs use surfaces that introduce an asymmetry to this oscillation cycle. Unlike surface tension driven DMFs, these systems move droplets through an imbalance of pinning forces on the edges of the contact line.
Anisotropic ratchet conveyors
Anisotropic ratchet conveyors (ARCs) use two sources of asymmetry: a heterogeneous surface pattern and a difference in pinning forces during dewetting compared to wetting22,33,34. The ARC surface pattern consists of a path of arcs or curved “rungs” surrounded by a hydrophobic border (Figure 1d) and it can be texture or chemical based. In texture ARCs, the rungs are patterned mesas surrounded by a trench, and the hydrophobic region is created by an array of pillars22,33. This topography induces a superhydrophobic state, or Cassie–Baxter state35, as air is trapped under the droplet in the trenches between rungs. Chemical ARCs, by contrast, are composed of alternating hydrophobic and hydrophilic rungs on a flat surface34. Applied vertical vibrations cause the contact line of a droplet to oscillate along the path of rungs. The contact line expands relatively equally in both directions, as the wetting process is less sensitive to ARC surfaces22,34. However, during the dewetting process, when the contact line recedes, the leading edge of the contact line experiences higher pinning forces than the receding edge due to the conforming shape of the rungs22. This phenomenon is described by Equation (6)34, where χlead and χtrail are the line fractions of the leading and trailing edges, respectively, that pin to the rungs, w is the width of the drop projected orthogonally to the pinning direction; and θ1 and θ2 are the equilibrium contact angles of the relatively hydrophilic rungs and relatively hydrophobic region between rungs, respectively.
The difference in pinning between the two edges results in a net force, especially during the contracting phase of oscillation22,34. Equation (6) shows the difference between the forces on the leading edge (Flead) and the trailing edge (Ftrail) of the droplet. If we instead look at the ratio (Ftrail/Flead) of these opposing forces, we obtain Equation (7), which shows the four components that account for the anisotropy in ARC systems: the two contact angles θ1 and θ2 and the line fractions χlead and χtrail on each edge of the droplet. The rung pattern causes the line fraction to be larger on the leading edge of the droplet, without which the forces would be equal on both edges of the droplet, and no net motion would occur (Figure 1e).
Both texture and chemical ARCs are fabricated by a single mask process. For texture ARCs, silicon or glass wafers are patterned with photoresist and etched with a deep reactive-ion etching (RIE) system to create the trenches and rungs. The ARCs are then coated with a hydrophobic silane to prevent the droplets from infiltrating the trenches33,34. Texture ARCs can also be fabricated out of polydimethylsiloxane (PDMS) by using a silicon or glass wafer etched with the pattern negative as a mold36. Chemical ARCs are fabricated using a similar process, but the wafers are first coated with a relatively hydrophilic layer of trimethylsilanol (TMS). The surface pattern is formed with photoresist and by etching exposed regions of TMS with oxygen plasma. The hydrophobic regions are then created with a silane (perfluorooctyltrichlorosilane) or with gold and dodecanethiol34.
Nanostructured Parylene
Nanostructured Parylene ratchets are composed of a Parylene film made of tilted nanorods (Figure 1f)37. Unlike ARCs, the asymmetry of the Parylene ratchets does not come from a surface pattern, but rather the angle of the nanorods. This geometry provides an anisotropic wetting effect on the droplet. The contact angles on the advancing (θA) and receding (θR) edges of a droplet on these nanofilms exhibit a directional dependence, which results in a net force37. The ratio of forces on opposing edges of the droplet is shown in Equation (8)37.
Droplet transport is induced by vertical vibrations, as in ARCs, which cause the contact line to oscillate37. Interestingly, this model is similar to the model for ARC systems shown in Equation (7). However, the line fraction is the same on both edges of the droplet, and the four components that account for the anisotropy in this system are all contact angles, two on each edge of the droplet. In this case, the net force results from the difference in the contact angles induced by the angle of the nanorods. Removing the tilt of the nanorods results in no net force, as the respective contact angles are the same on each edge of the droplet (Figure 1g). The similarity between the models for ARC and nanostructured Parylene systems presents the interesting possibility of combining the key features of each platform. For example, a tilt could be introduced to the rungs in the ARC system, or a nanostructured Parylene device could be fabricated with an ARC surface pattern. Such a combination could potentially provide dramatic improvements in the transport efficiency of these systems.
Nanostructured Parylene ratchets are fabricated using a technique called vapor deposition polymerization (VDP)23. This deposition process is different from the commonly used process of physical vapor deposition, because the reactive monomers can only bind to the end of the polymer chain in VDP23. This results in high aspect ratio Parylene rods with a nano-scale diameter. To create the angular structure of the Parylene ratchets, the substrate is tipped at an angle with respect to the incident vapor flux23,37 during the VDP.
Tilted pillar arrays
Tilted pillar arrays (TPAs) use silicon pillars arranged in an angular nano- or micro-structure to control the contact line pinning of a vibrated droplet (Figure 1h)24. Much like nanostructured Parylene ratchets, the titled pillars create differences between the contact angles on the leading and trailing edges, resulting in a net force that moves the droplet through cycles of contact line oscillation24. Interestingly, droplets move with the direction of the tilt on nanostructured pillars, but move against the direction of the tilt on microstructured pillars24. This observation suggests that it would be useful to combine titled structures and surface patterns in contact line driven DMF systems. It would be interesting to understand how the direction of the tilt competes with the surface pattern. For example, if a tilted microstructure is in the same direction as the surface pattern, the net forces from the two anisotropies may cancel out and transport would not be possible. However, if the structures are combined so the net forces are in the same direction, than the transport efficiency may be increased, as described in the previous section.
Fabrication of TPAs begins with a silicon wafer substrate, the pattern for nanostructured TPAs is formed by using a metal, thin-film dewetting process24,38, whereas the pattern for microstructured TPAs is formed by conventional photolithography. In both cases, the silicon wafer is etched using “glancing-angle” RIE, wherein the substrate is tilted at a 70° angle inside an RIE chamber24,38. Once the tilted pillars have been etched into the substrate, the surface is then functionalized with a silane coating24,38.
Functions with Droplets
In addition to moving the droplets, DMF systems are also capable of performing specific functions on the droplets. Key functions that DMF systems perform are generation, switching, fusion, and fission.
Generation
Droplet generation describes the process in which individual droplets of a reproducible size are pulled from a large reservoir. This function allows for a large sample to be divided into many smaller parts, which increases the number of reactions or tests that can be performed with a single sample. DMF systems also require a sample to be divided into small droplets. Without this function, a sample has to be distributed into smaller droplets through manual pipetting or with a separate apparatus. Thus far, droplet generation has been reported in electrowetting (EWOD39 and OEW25) and ARC36 systems.
EWOD systems generate droplets by first activating a pair of electrodes near the meniscus (edge) of a reservoir (Figure 2a). The meniscus is then pulled further from the reservoir by sequentially activating electrode pairs in line with the first pair39. The location where the droplet separates from the reservoir determines the size of the generated droplet, but it is dependent on the initial shape of the meniscus, which is not predictable. However, the shape of the meniscus in the region near the first electrode pair can be stabilized with “side electrodes”. The side electrodes are placed on either side of the path formed by the initial electrode pairs. This design allows for relatively uniform droplets to be produced, with a volume of 2 to 3 µL39. OEW systems perform this function based on similar principles, but with a light beam that activates electrodes adjacent to the reservoir, pulling a droplet on the active OEW region25. The sizes of the generated droplets are similar to the spot size of the beam25.
Droplet generation and switching. (a) EWOD (adapted with permission from Ref 39 Copyright 2003 IEEE) and (b) ARC systems can generate droplets by pulling liquid from a large reservoir (adapted with permission from Ref 36 Copyright 2008 IEEE). (c) Microheater intersections can also selectively switch droplets (adapted with permission from Ref 40 Copyright 2003 AIP Publishing LLC). (d) EWOD switches can be integrated in ARC devices (adapted with permission from Ref 41 Copyright 2009 IEEE).
Droplet generation for ARCs is possible using a pattern of concentric circles alternating between mesas and trenches36. Like smaller droplets, the contact line of this reservoir will oscillate in response to vertical vibrations of sufficient amplitude. As the vibration amplitude is increased over a second threshold, the morphology of the contact line will shift from a nearly perfect circle to a trigonal planar shape32,36. The alternating circle pattern distorts or modifies this contact line, which introduces instabilities at the “vertices” of the contact line36. As the contact line expands across the surface texture, the vertices become pinned on the mesas. When the contact line retracts, a “pinch-off” occurs as the contact line is sheared over the trench (Figure 2b). With this design, the resulting droplet size is dependent on the initial size of the reservoir, and droplets as small as 0.1 µL have been generated36.
Switching
Switching is the process of selectively moving a droplet from one path to another. This function is essential for sorting droplets and increasing the throughput of downstream processes. Switches are relatively simple to implement with DMF systems that move droplets by modulating surface tension because a surface tension gradient can be created in any direction within the droplet. On an EWOD or OEW device, a droplet will move in the direction of an activated electrode. With an array of individually addressable electrodes, a droplet can be switched by activating an electrode next to the current path of the droplet7,25,39. The droplet will be pulled onto this electrode and can be subsequently directed to a new path in any direction. Microheaters are also organized in individually addressable arrays to move droplets, but unlike EWOD electrodes, individual microheaters can only move droplets along a single axis40. However, microheater switches have been achieved through the use of specially designed “intersections”. These intersections can switch a droplet by turning it 90 degrees onto a new track (Figure 2c). The intersection accomplishes this by creating a heated region that pushes the droplet in the direction of the new path while inhibiting movement on the direction of the original path40. With photosensitive surfaces, as in electrowetting, droplets can be directed in any direction or pattern depending on the location of the light-activated chemical gradient relative to the droplet21,31.
Implementing switches on contact line driven systems has been proven to be more of a challenge. ARC systems have been developed that use EWOD electrodes to pull droplets onto a new path of rungs (Figure 2d)41. However, a switch that selectively moves droplets solely through geometric modulation of the contact line has yet to be developed. Interestingly, ARC systems are able to selectively move specific droplet sizes based on the frequency of applied vibrations42. This ability is likely present in nanostructured Parylene ratchets and TPAs as well, as the amplitude threshold for contact line oscillation is based on droplet volume43. As mentioned previously, the direction of droplet motion is also dependent on the feature size of the TPAs. Such phenomena could eventually lead to the production of a switch that relies only on the geometric control of the contact line.
Droplet fusion
The fusion, or merging, of two droplets is a simple function for DMF systems to perform. With no encapsulating liquid, two droplets will spontaneously merge when they come in contact. Surface tension driven systems can accomplish this by creating surface tension gradients in two droplets that are directed towards each other, which causes the droplets to converge (Figure 3a)39. Droplet fusion can be accomplished on contact line driven systems in a similar fashion by transporting droplets along two converging paths22. Fusion can also be performed along a single path with two different sized droplets (Figure 3b). This is accomplished by using a vibration frequency that modulates the contact line of only one droplet. One droplet will be transported along the path while the other remains static. When the moving droplet reaches the static droplet, the two will merge, and the resulting droplet can then be transported using a different vibration frequency22.
Droplet fission and fusion. (a) The sequence depicts the fission of one large droplet into two smaller droplets, and the recombination of the two droplets (adapted with permission from Ref 39 Copyright 2003 IEEE). (b) Two droplets are merged on an ARC path, and the resulting droplet is then transported (adapted with permission from Ref 22 Copyright 2012 John Wiley & Sons). (c) Microheater arrays can split droplets by creating thermal gradients (adapted with permission from Ref 40 Copyright 2003 AIP Publishing LLC).
Although droplets can merge spontaneously, this does not guarantee that the resulting droplet will be homogeneously mixed. Homogeneity in the resulting droplet will eventually occur through diffusion, but this is a relatively slow process. This process can be hastened on electrowetting devices through a series of “mixing steps” wherein the droplet is moved back and forth between two electrodes or electrode pairs44. This mixing step is not necessary on microheater arrays because the thermocapillary convection currents that move the droplet also mix a fused droplet40. Similarly, in contact line driven systems, the applied vertical vibrations drive the droplets with a cyclical motion, which also aids in mixing fused droplets22.
Droplet fission
Once two droplets have been fused and mixed, it may be desirable to divide the resulting droplet for multiple, subsequent uses. Therefore, the ability to perform droplet fission, or split the droplet into two or more smaller droplets, is very useful for DMF systems. Droplet fission has been accomplished with EWOD, OEW, and microheater systems. With EWOD, droplets can be split by activating electrodes on two opposing edges of the droplet, and by turning off the electrode beneath the center of the droplet. This pulls the edges of the droplet apart and causes the center of the droplet to neck, pinching apart the droplet (Figure 3a)39. OEW devices perform droplet fission the same way, using two light beams to activate electrodes on opposing droplet edges25. Droplet fission on microheater arrays occurs in a similar fashion, but microheaters in the center of the droplet are activated. This induces a diverging Marangoni flow, which thins the center of the droplet40. Necking occurs as the droplet center thins, leading to eventual pinch-off and the formation of two new droplets (Figure 1c)40.
Droplet fission has yet to be achieved with contact line driven systems. Transport in contact line driven systems is possible because the force acting on the leading edge of the droplet is larger than the force acting on the trailing edge. Splitting a droplet requires nearly equal forces acting on two opposing edges. These forces must also be large enough to overcome the surface tension of the droplet and persist long enough for the necking region to reach pinch-off45. Electrowetting and microheater systems can maintain such a force for an indefinite amount of time, whereas contact line driven systems can only provide this force during one-half of the contact line oscillation cycle (the contracting phase). However, the time required for droplet pinch-off is dependent on the diameter of the necking region45. Therefore, contact line driven systems could potentially perform droplet fission if a surface pattern could induce a contact line geometry with a small necked region. Additionally, it may be possible for a surface pattern to create a necking region that induces a resonance with an increasing transient response. In that case, the diameter of the neck would be reduced during each cycle of oscillation until pinch-off.
Applications of DMF Systems
DMF systems can be used for many of the same applications as segmented flow microfluidic systems. Although DMF systems operate with larger droplets and slower throughput, the ability to selectively control individual droplets makes DMF systems better suited for some applications (e.g., combinatorial chemistry7). Furthermore, these DMF systems move droplets through interactions with the substrate surface. Although this raises issues involving solute–surface interactions, it also provides an opportunity to address unique applications. For example, droplets can be moved to temperature sensitive regions on a chip or surface to aid in thermal management46,47. The movement of droplets along a surface could be used to pick up and remove undesired particulates, serving as a self-cleaning surface48, or to transport desirable particulates deposited onto a surface49.
EWOD was the first DMF system to be introduced, and it therefore has the most best-developed toolbox. EWOD devices have already been tested in applications such as cell isolation and analysis50, bioassays51, and DNA analysis52,53. Despite this success, a major criticism of EWOD technology is the complex circuitry that is required to address individual electrodes in an array6,7. Driving droplets on microheater arrays and photosensitive chemical gradient surfaces also requires relatively complex circuitry or off-chip control systems. However, a more recent type of OEW system called single-sided continuous optoelectrowetting (SCOEW) uses a continuous layer of photoconductive amorphous silicon instead of a pixilated grid of electrodes to perform electrowetting. This system can also drive droplets with light produced from a liquid crystal display54. Additionally, contact line driven systems only require an externally applied vibration to move droplets. Continued development of these more recently conceived systems could lead to a platform that can more efficiently address many applications. Hybrid DMF systems are also possible41. These would combine features of multiple DMF systems and could potentially lead to the realization of a robust platform for micro-total analysis and lab-on-a-chip systems.
Another field of microfluidics, known as paper or paper-based microfluidics, involves transporting liquids using capillary forces (paper wicking) in channels defined by hydrophobic barriers55,56. These devices can be made from relatively inexpensive materials and do not require external stimuli to function. These properties have attracted attention for applications requiring low-cost analytical platforms (e.g., health care diagnostics, environmental monitoring, food quality control, and forensics)55,56. However, paper microfluidics are limited by poor efficiency; large portions of a sample are often retained in the channel or lost to evaporation during transport56. Many paper microfluidic systems also use a colorimetric detection method that usually has a high limit of detection56. This approach prevents these systems from accurately measuring solutions with low analyte concentrations. The complexity of most surface tension driven DMF systems may become cost- or resource-prohibitive, but SCOEW shows great potential for low-cost diagnostic and analytic systems. The low power requirements and ability to drive droplets with a liquid crystal display make this system a good candidate for portable diagnostic systems. Additionally, contact line driven DMF systems require only a passive surface architecture and a vertical vibration. These surfaces can be made from many different materials, and the required vibrations are within the parameters of commercially available speakers found in cellular phones22,24,49, which have become virtually ubiquitous and can be easily transported. DMF systems transport droplets as an entire self-contained entity, which avoids issues of sample retention experienced by paper microfluidic systems. Additionally, this property allows for integration with many detection systems, as the entire droplet can be transported onto a desired detection region. Implementing sensitive detectors with DMF systems could enable applications requiring detection limits outside the capabilities of paper microfluidic devices. These DMF systems could serve as a more efficient platforms for low-cost analytical devices, or they could be combined with paper microfluidic detection zones to improve the transport efficiency.
Conclusion
As of today, four main categories compose the field of microfluidics: continuous flow, segmented flow, paper, and digital. Continuous flow systems transport liquid through channels in a laminar flow regime. Segmented flow systems reduce reactant quantities by transporting fluid in discrete droplets separated by an immiscible fluid. Both continuous and segmented flow systems can operate at very high throughputs but require complicated pump systems. Paper microfluidics provide a simpler, inexpensive platform, but are limited by poor transport efficiency. DMF systems fill the gap between segmented flow and paper systems, operating with larger droplets and slower throughputs than segmented flow systems but with higher efficiency than paper systems. DMF systems also have the unparalleled ability to selectively control individual droplets.
DMF systems can transport and manipulate droplets through surface anisotropy. EWOD, microheater arrays, and chemical gradient systems move droplets by modulating surface tension, whereas ARC, nanostructured Parylene, and TPA systems guide the contact line of a droplet. Both surface tension and contact line driven systems can perform droplet generation and fusion. However, only surface tension driven systems can currently perform switching and fission functions. Developing methods to perform these functions on contact line driven systems is still an open problem for researchers in the field.
In the future, the ability of DMF systems to individually control and selectively perform functions on droplets will be essential for building true lab-on-a-chip systems. DMF devices will also serve as platforms for low-cost analytical systems, because their transport efficiency and capacity for digital integration can be useful in applications outside the capabilities of paper microfluidic systems.
Notes
†The original subscripts PIN and REL37 were changed to trail and lead, respectively, to maintain consistency between equations.
References
Umbanhowar PB, Prasad V, Weitz DA . Monodisperse emulsion generation via drop break off in a coflowing stream. Langmuir 2000; 16: 347–351.
Anna SL, Bontoux N, Stone HA . Formation of dispersions using ‘flow focusing’ in microchannels. Applied Physics Letters 2003; 82: 364–366.
Thorsen T, Roberts RW, Arnold FH et al. Dynamic pattern formation in a vesicle-generating microfluidic device. Physical Review Letters 2001; 86: 4163.
Solvas XCI, deMello A . Droplet microfluidics: Recent developments and future applications. Chemical Communications 2011; 47: 1936–1942.
Teh S-Y, Lin R, Hung L-H et al. Droplet microfluidics. Lab on a Chip 2008; 8: 198–220.
Theberge AB, Courtois F, Schaerli Y et al. Microdroplets in microfluidics: An evolving platform for discoveries in chemistry and biology. Angewandte Chemie International Edition 2010; 49: 5846–5868.
Abdelgawad M, Wheeler AR . The digital revolution: A new paradigm for microfluidics. Advanced Materials 2009; 21: 920–925.
Agresti JJ, Antipov E, Abate AR et al. Ultrahigh-throughput screening in drop-based microfluidics for directed evolution. Proceedings of the National Academy of Sciences of the United States of America 2010; 107: 4004–4009.
Abate AR, Hung T, Mary P et al. High-throughput injection with microfluidics using picoinjectors. Proceedings of the National Academy of Sciences of the United States of America 2010; 107: 19163–19166.
Brouzes E, Medkova M, Savenelli N et al. Droplet microfluidic technology for single-cell high-throughput screening. Proceedings of the National Academy of Sciences of the United States of America 2009; 106: 14195–14200.
Mazutis L, Gilbert J, Ung WL et al. Single-cell analysis and sorting using droplet-based microfluidics. Nature Protocols 2013; 8: 870–891.
Huebner A, Bratton D, Whyte G et al. Static microdroplet arrays: A microfluidic device for droplet trapping, incubation and release for enzymatic and cell-based assays. Lab on a Chip 2009; 9: 692–698.
Huebner A, Srisa-Art M, Holt D et al. Quantitative detection of protein expression in single cells using droplet microfluidics. Chemical Communications 2007; 12: 1218–1220.
Zheng B, Roach LS, Ismagilov RF . Screening of protein crystallization conditions on a microfluidic chip using nanoliter-size droplets. Journal of the American Chemical Society 2003; 125: 11170–11171.
Song H, Chen DL, Ismagilov RF . Reactions in droplets in microfluidic channels. Angewandte Chemie International Edition 2006; 45: 7336–7356.
deMello AJ . Control and detection of chemical reactions in microfluidic systems. Nature 2006; 442: 394–402.
Lee J, Moon H, Fowler J et al. Electrowetting and electrowetting-on-dielectric for microscale liquid handling. Sensors and Actuators A 2002; 95: 259–268.
Mugele F, Baret J-C . Electrowetting: From basics to applications. Journal of Physics: Condensed Matter 2005; 17: R705.
Pollack MG, Fair RB, Shenderov AD . Electrowetting-based actuation of liquid droplets for microfluidic applications. Applied Physics Letters 2000; 77: 1725–1726.
Darhuber AA, Valentino JP, Troian SM et al. Thermocapillary actuation of droplets on chemically patterned surfaces by programmable microheater arrays. Journal of Microelectromechanical Systems 2003; 12: 873–879.
Lim HS, Han JT, Kwak D et al. Photoreversibly switchable superhydrophobic surface with erasable and rewritable pattern. Journal of the American Chemical Society 2006; 128: 14458–14459.
Duncombe TA, Erdem EY, Shastry A et al. Controlling liquid drops with texture ratchets. Advanced Materials 2012; 24: 1545–1550.
Demirel MC . Emergent properties of spatially organized poly(p-xylylene) films fabricated by vapor deposition. Colloids and Surfaces A: Physicochemical and Engineering Aspects 2008; 321: 121–124.
Agapov RL, Boreyko JB, Briggs DP et al. Length scale selects directionality of droplets on vibrating pillar ratchet. Advanced Materials Interfaces 2014; 1: 1400337.
Chiou P-Y, Chang Z, Wu MC . Droplet manipulation with light on optoelectrowetting device. Journal of Microelectromechanical Systems 2008; 17: 133–138.
Brochard F . Motions of droplets on solid surfaces induced by chemical or thermal gradients. Langmuir 1989; 5: 432–438.
Brzoska JB, Brochard-Wyart F, Rondelez F . Motions of droplets on hydrophobic model surfaces induced by thermal gradients. Langmuir 1993; 9: 2220–2224.
Hazlett RD . Fractal applications: Wettability and contact angle. Journal of Colloid and Interface Science 1990; 137: 527–533.
Chaudhury MK, Whitesides GM . How to make water run uphill. Science 1992; 256: 1539–1541.
Ichimura K, Oh S-K, Nakagawa M . Light-driven motion of liquids on a photoresponsive surface. Science 2000; 288: 1624–1626.
Kekkonen V, Hakola A, Kajava T et al. Self-erasing and rewritable wettability patterns on ZnO thin films. Applied Physics Letters 2010; 97: 044102.
Noblin X, Buguin A, Brochard-Wyart F . Vibrated sessile drops: Transition between pinned and mobile contact line oscillations. European Physical Journal E: Soft Matter 2004; 14: 395–404.
Shastry A, Taylor D, Böhringer KF . Micro-structured surface ratchets for droplet transport. The 14th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS'07); 10–14 June 2007, Lyon, France; 2007: 1353–1356.
Duncombe TA, Parsons JF, Böhringer KF . Directed drop transport rectified from orthogonal vibrations via a flat wetting barrier ratchet. Langmuir 2012; 28: 13765–13770.
Whyman G, Bormashenko E, Stein T . The rigorous derivation of Young, Cassie–Baxter and Wenzel equations and the analysis of the contact angle hysteresis phenomenon. Chemical Physics Letters 2008; 450: 355–359.
Erdem EY, Baskaran R, Bohringer KF . Vibration induced droplet generation on textured surfaces. IEEE the 21st International Conference on Micro Electro Mechanical Systems (IEEE MEMS2008); 13–17 Jan 2008, Tucson, AZ, USA; 2008: 603–606.
Malvadkar NA, Hancock MJ, Sekeroglu K et al. An engineered anisotropic nanofilm with unidirectional wetting properties. Nature Materials 2010; 9: 1023–1028.
Agapov RL, Srijanto B, Fowler C et al. Lithography-free approach to highly efficient, scalable SERS substrates based on disordered clusters of disc-on-pillar structures. Nanotechnology 2013; 24: 505302.
Cho SK, Moon H, Kim C-J . Creating, transporting, cutting, and merging liquid droplets by electrowetting-based actuation for digital microfluidic circuits. Journal of Microelectromechanical Systems 2003; 12: 70–80.
Darhuber AA, Valentino JP, Davis JM et al. Microfluidic actuation by modulation of surface stresses. Applied Physics Letters 2003; 82: 657–659.
Duncombe TA, Kumemura M, Fujita H et al. Integrating EWOD with surface ratchets for active droplet transport and sorting. IEEE the 22st International Conference on Micro Electro Mechanical Systems (IEEE MEMS2009); 25–29 Jan 2009; Sorrento, Italy; 2008: 531–534.
Varel C, Bohringer KF . Liquid droplet micro-bearings on directional circular surface ratchets. IEEE the 27st International Conference on Micro Electro Mechanical Systems (IEEE MEMS2014); 26–30 Jan 2014; San Francisco, CA, USA; 2014: 983–986.
Bauer HF, Chiba M . Oscillations of captured spherical drop of viscous liquid. Journal of Sound and Vibration 2005; 285: 51–71.
Lu HW, Bottausci F, Fowler JD et al. A study of EWOD-driven droplets by PIV investigation. Lab on a Chip 2008; 8: 456–461.
Burton JC, Rutledge JE, Taborek P . Fluid pinch-off dynamics at nanometer length scales. Physical Review Letters 2004; 92: 244505.
Cheng JT, Chen C-L . Active thermal management of on-chip hot spots using EWOD-driven droplet microfluidics. Experiments in Fluids 2010; 49: 1349–1357.
Gong J, Cha G, Ju YS et al. Thermal switches based on coplanar EWOD for satellite thermal control. IEEE the 21st International Conference on Micro Electro Mechanical Systems (IEEE MEMS2008); 13–17 Jan 2008; Tucson, AZ, USA; 2008: 848–851.
Jönsson-Niedziólka M, Lapierre F, Coffinier Y et al. EWOD driven cleaning of bioparticles on hydrophobic and superhydrophobic surfaces. Lab on a Chip 2011; 11: 490–496.
Sekeroglu K, Gurkan UA, Demirci U et al. Transport of a soft cargo on a nanoscale ratchet. Applied Physics Letters 2011; 99: 063703.
Shah GJ, Ohta AT, Chiou EPY et al. EWOD-driven droplet microfluidic device integrated with optoelectronic tweezers as an automated platform for cellular isolation and analysis. Lab on a Chip 2009; 9: 1732–1739.
Vergauwe N, Witters D, Ceyssens F et al. A versatile electrowetting-based digital microfluidic platform for quantitative homogeneous and heterogeneous bio-assays. Journal of Micromechanics and Microengineering 2011; 21: 054026.
Lin T-H, Yao D-J . Applications of EWOD systems for DNA reaction and analysis. Journal of Adhesion Science and Technology 2012; 26: 1789–1804.
Jary D, Chollat-Namy A, Fouillet Y et al. DNA repair enzyme analysis on EWOD fluidic microprocessor. Technical Proceedings of the NSTI Nanotechnology Conference and Trade Show; 7–11 May 2006; Boston, USA; 2006: 554–557.
Park SY, Teitell MA, Chiou EPY . Single-sided continuous optoelectrowetting (SCOEW) for droplet manipulation with light patterns. Lab on a Chip 2010; 10: 1655–1661.
Mao X, Huang TJ . Microfluidic diagnostics for the developing world. Lab on a Chip 2012; 12: 1412–1416.
Li X, Ballerini DR, Shen W . A perspective on paper-based microfluidics: Current status and future trends. Biomicrofluidics 2012; 6: 011301.
Acknowledgements
This work was supported by National Science Foundation grant ECCS-1308025 “Droplet Ratchets: Low Cost Digital Microfluidics. HRH would like to acknowledge the National Defense Science and Engineering Graduate Fellowship (NDSEG) for their support of this work. Fabrication of ARCs was performed at the Washington Nanofabrication Facility (WNF), a National Nanotechnology Coordinated Infrastructure (NNCI) site at the University of Washington, which is supported in part by the National Science Foundation (awards 1542101, 1337840 and 0335765), the Washington Research Foundation, the M. J. Murdock Charitable Trust, Altatech, ClassOne Technology, GCE Market, Google and SPTS.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 Unported License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Holmes, H., Böhringer, K. Transporting droplets through surface anisotropy. Microsyst Nanoeng 1, 15022 (2015). https://doi.org/10.1038/micronano.2015.22
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/micronano.2015.22
This article is cited by
-
Picoliter droplet array based on bioinspired microholes for in situ single-cell analysis
Microsystems & Nanoengineering (2020)