Abstract
Two-dimensional (2D) materials have emerged as promising candidates for miniaturized optoelectronic devices due to their strong inelastic interactions with light. On the other hand, a miniaturized optical system also requires strong elastic light–matter interactions to control the flow of light. Here we report that a single-layer molybdenum disulfide (MoS2) has a giant optical path length (OPL), around one order of magnitude larger than that from a single-layer of graphene. Using such giant OPL to engineer the phase front of optical beams we have demonstrated, to the best of our knowledge, the world’s thinnest optical lens consisting of a few layers of MoS2 less than 6.3 nm thick. By taking advantage of the giant elastic scattering efficiency in ultra-thin high-index 2D materials, we also demonstrated high-efficiency gratings based on a single- or few-layers of MoS2. The capability of manipulating the flow of light in 2D materials opens an exciting avenue towards unprecedented miniaturization of optical components and the integration of advanced optical functionalities. More importantly, the unique and large tunability of the refractive index by electric field in layered MoS2 will enable various applications in electrically tunable atomically thin optical components, such as micro-lenses with electrically tunable focal lengths, electrical tunable phase shifters with ultra-high accuracy, which cannot be realized by conventional bulk solids.
Similar content being viewed by others
Introduction
Interactions between light and matter can be divided into two categories: inelastic and elastic1. An inelastic interaction involves energy transfer between photons and electrons or phonons. In contrast, elastic interactions do not involve energy transfer and are responsible for controlling the propagation of light. Optical components, such as resonant cavities, waveguides, lenses, gratings, and, more recently, optical meta-materials2 and photonic crystals3, all rely on strong elastic interactions between light and matter to achieve sophisticated control of the flow of light. Strong elastic interactions rely on significant changes of the amplitude and phase of the light accumulated over a long optical path and, hence, for very thin materials, such as a two-dimensional(2D) graphene sheet, the interaction is generally very small4. Considerable effort has been devoted to this issue, but success has been only achieved in the mid- to far-infrared where the plasmonic resonance in graphene can enhance the elastic optical response5,6,7. It remains a great challenge to manipulate the flow of light using atomically thin 2D materials in the important visible and near-infrared spectral regions where 2D materials have most interesting optoelectronic properties8,9,10,11,12,13,14,15,16,17,18,19. Rather surprisingly, as we will show later, the strength of the elastic interaction in a thin 2D material increases dramatically with increasing refractive index because of the unique geometry associated with an ultra-thin film. Such favorable scaling makes high-index transition-metal dichalcogenide (TMD) 2D semiconductors11,20,21,22, such as molybdenum disulfide(MoS2), particularly attractive for strong elastic light–matter interactions.
Materials and methods
Device fabrication and characterization
For the phase-shifting interferometry (PSI) measurements, single- and few-layer TMD semiconductors and graphene were deposited onto a SiO2/Si substrate (275 nm thermal SiO2) by mechanical exfoliation using 3M scotch tape. All Raman and photoluminescence (PL) measurements were conducted with a Horiba Jobin Yvon T64000 micro-Raman/PL system, with a 532 nm Nd:YAG green laser for excitation. All the optical path length (OPL) characterizations were obtained using a Veeco NT9100 phase-shifting interferometer. The atomically thin micro-lens and gratings were fabricated in a FEI Helios 600 NanoLab focused ion beam (FIB) system (Gallium ion source) using pre-calibrated dosage, optimized beam voltage (30 kV) and beam current (9.7 pA). The gratings and micro-lens were characterized using a green laser with a wavelength of 532 nm.
Numerical simulation
Rigorous coupled-wave analysis (RCWA) was used to calculate the phase delay and grating efficiency. The method numerically solves Maxwell’s equations in multiple layers of structured materials by expanding the field in Fourier space. The finite element method was used to calculate the optical scattering cross-section of the nano ribbons.
Results and discussion
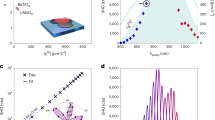
Refractive optical components rely on the OPL to modify the phase front of an optical beam. The OPL is directly related to the geometrical length of the light path. As a result, it is normally expected that the OPL of a monolayer of a 2D material would be too small to have a significant impact on the phase front because the layer is so thin. However, here we measured a giant OPL of 38 nm from a single-layer MoS2, which is more than 50 times larger than its physical thickness of 0.67 nm and around one order of magnitude larger than the measured OPL of a single-layer graphene that was found to be only 4.4 nm (Figure 1).
Giant optical path lengths (OPLs) from single- and few-layer MoS2. (a) Optical microscope image of a mechanically exfoliated MoS2 sample on a SiO2/Si substrate (275 nm thermal SiO2). Different contrasts correspond to MoS2 flakes of different thicknesses. The areas labeled as “1L”, “2L”, “3L,”and “4L” are single-, bi-, triple-, and quadruple-layer MoS2, respectively. (b) Phase shifting interferometry (PSI) image of the region inside the box indicated by the dashed line in (a). (c) PSI-measured OPL values versus position for 1L, 2L, 3L, and 4L MoS2 along the dashed line in (b). (d) Statistical data of the OPL values from PSI for 1L, 2L, 3L, and 4L MoS2 and graphene samples. For each layer number of MoS2 and graphene, at least five different samples were characterized for the statistical measurements. Inset is the schematic plot showing the PSI-measured phase shifts of the reflected light from the MoS2 flake and the SiO2 substrate (). (e) Atomic force microscopy (AFM) image of 1L and 2L MoS2 from the box enclosed by the dashed line 1 in (b). (f) AFM image of 3L and 4L MoS2 from box enclosed by the dashed line 2 in (b).
In our experiments, single- or few-layer MoS2 flakes were transferred onto a silicon wafer with 275 nm of surface thermal oxide by mechanical exfoliation4,7. The flakes were firstly identified by their optical contrast in an optical microscope. Regions with different colors corresponded to MoS2 flakes with different thicknesses (Figure 1a). Due to their high refractive index, these atomically thin MoS2 layers have significant and layer-dependent OPL values and this enables the layers to be easily identified by phase-shifting interferometry (PSI) (Figure 1b and 1c). PSI is capable of measuring the vertical OPL to an accuracy of around 0.1 nm, by analyzing the digitized interference pattern obtained during a well-controlled phase shift (Supplementary Fig. S1 and S2). The measured OPL value of the MoS2 flake on a SiO2 substrate at 535 nm was determined by:

where λ is the wavelength of the light source, and are the PSI-measured phase shifts of the light reflected from the MoS2 flake and the SiO2 substrate (Figure 1d inset), respectively. We characterized multiple samples and obtained statistical values of the OPL for single- and few-layer MoS2 samples as shown in Figure 1d. For each number of layers of MoS2, at least five different samples were characterized in these statistical measurements. The layer number could be quickly determined by the measured layer-dependent OPL values and the deduced layer number was confirmed by corresponding atomic force microscopy (AFM) images (Figure 1e and 1f); Raman microscopy (Supplementary Fig. S3a); and PL measurements (Supplementary Fig. S3b) on the same samples. For comparison, we performed the same characterizations on mechanically exfoliated graphene samples (Figure 1d and Supplementary Fig. S4, S5, and S6). The measured average and standard deviation error of the OPL values from 1L, 2L, 3L, and 4L MoS2 samples were 38.0 ± 2.8 nm, 85.4 ± 2.2 nm, 124.0 ± 6.6 nm, and 162.6 ± 9.0 nm, respectively, while those from 1L, 2L, 3L, and 4L graphene samples were 4.4 ± 0.8 nm, 8.2 ± 2.0 nm, 13.0 ± 3.2 nm, and 17.2 ± 3.6 nm, respectively, indicating that MoS2 has an OPL per layer approximately an order of magnitude larger than graphene.
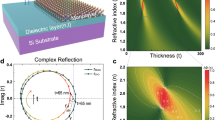
This giant OPL is created by relatively strong multiple reflections at the air-MoS2 and MoS2–SiO2 interfaces. We consider a simple interface between air and SiO2, each occupying half infinite space. A layer of 2D material with a real refractive index n is placed in between the two media. The high impedance mismatch at these interfaces leads to large reflection coefficients, which cause the strong multiple reflections of light in the 2D material(Figure 2a). The amplitude of the reflected light is the summation of the multiple reflections off the interfaces of the thin high index layerRi, where i indicates the number of round trips in the 2D material. As the index increases so does the reflectivity of the interfaces, which increases the effective number of transits of the light through the high index layer and thus the OPL of the reflected light (Figure 2a). We verify this intuition with numerical calculation as shown by the dashed line in Figure 2c. The magnitude of OPL difference comparing with and without the 2D material on SiO2 (Supplementary Fig. S7) increases rapidly with increasing n. The OPL is low for low-index 2D materials, where the small reflection coefficients cause Ri to be small. This situation in illustrated schematically in Figure 2b. Additionally, in the experiment, we used a silicon substrate with a layer of 275 nm thermal SiO2 on its surface, which forms a weak Fabry-Perot resonance. As a result of this weak resonant enhancement, the OPL is further enhanced by a factor of around 1.5 as shown by the solid line in Figure 2c. Figure 2c also shows the OPL for a few other materials. The OPL of high-index 2D materials, such as MoS2, is remarkably larger than that of SiO2, graphene, Au or Si. The wavelength used for these calculations was 535 nm. The refractive indices used for single-layer MoS223, silicon, graphene24, SiO2, and Au were 4.4 + 0.6i, 4.15+0.044i, 2.6+1.3i, 1.46, and 0.47 + 2.4i, respectively. In order to approximate our simulation to the actual condition, for 2L MoS2, the refractive index in our simulation is assumed to be 4.4+0.6i (the index for 1L MoS2); for 3L and higher layer numbers, the refractive index is assumed to be 5.2+1.1i (the index for bulk MoS2)23. In addition, it should be noted that the giant OPL is not a narrow band effect. The calculated OPL for 1L MoS2 is above 20 nm at the wavelength ranging from 450 nm to 560 nm (Supplementary Fig. S8). The spectral position for highest OPL can be adjusted by changing the thickness of the SiO2.
High refractive index enabled giant OPL in ultra-thin film. (a and b) Schematic plots of multiple reflections at the interfaces of ultra-thin 2D materials. High refractive index leads to a large reflection coefficient. Light is reflected many times inside the material and leads to a highly enhanced light path, indicated as (a). For low refractive index material, the light path is much less enhanced because of the small reflection coefficient, indicated as (b). (c) Simulated OPL values for light reflected from 2D material (0.67 nm in thickness) with different indices on a SiO2 (275 nm)/Si substrate (solid line) and SiO2 substrate with infinite thickness (dashed line). The calculated OPLs of 0.67 nm Au, 0.67 nm SiO2, 1L (0.34 nm) graphene, and 1L (0.67 nm) MoS2 are represented by markers. (d) Simulated OPL values for 1L, 2L, 3L, and 4L MoS2 and graphene on SiO2 (275 nm)/Si substrate, respectively. The wavelength used in the simulations was 535 nm.
Even more remarkably, the OPL of single-, bi-, triple-, and quadruple-layer MoS2 scales almost linearly with the number of layers, offering the exciting opportunity of controlling the OPL using the number of layers of MoS2. When the layer thickness increases by 1 nm, the OPL increases by over 50 nm. Such a rapid change of OPL with thickness allows us to control the phase front of an optical beam very effectively using only an atomically thin structure. The theoretical and numerical predictions (Figure 2d) were well supported by the experimental data as shown in Figure 1d.
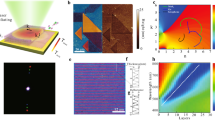
Next, we demonstrate phase-front engineering by fabricating the world’s thinnest lens based on a few atomic layers of MoS2 (Figure 3). We started with a flake of uniform 9L MoS2(6.28 nm in thickness, Supplementary Fig. S9) and then used FIB to mill a pre-designed bowl-shaped structure (20 μm in diameter) into the flake (Figure 3a and 3b). The gradual change of MoS2 thickness, from the center to the edge, led to a continuous and curved OPL profile for an incident beam, and this served as an atomically thin (reflective) concave micro-lens (Figure 3c). Based on the measured OPL profile, the focal length f of this MoS2 micro-lens was calculated to be –248 μm (Supplementary Fig. S10). In order to realize the precise design for this MoS2 micro-lens, we used the statistical calibration curve between the OPL values of MoS2 flakes and their layer numbers (Figure 3d). All the OPL values were measured by PSI and the layer numbers were confirmed by AFM. The OPL of MoS2 increased almost linearly with increasing the layer number when the layer number was less than five. We noticed the nonlinear response of OPL versus layer number when the layer number is more than five and this could be attributed to the fact that the single path absorption in MoS2 layer become more when the layer is thicker. Thus, the amplitude of the light will decrease faster in one round trip. When the amplitude of the light becomes very small after several roundtrips, its contribution to the OPL becomes negligible.
Atomically thin micro-lens fabricated from a few layers of MoS2. (a) PSI image of an atomically thin micro-lens fabricated on a 9L MoS2 flake. (b) Schematic plot of the micro-lens structure. The bowl-shaped structure of the micro-lens was fabricated by FIB milling with atomic resolution in the vertical direction and sub-20 nm resolution in lateral direction. (c) Measured OPL values versus position for the direction indicated by the dashed line in (a). (d) Measured statistical data of the OPL values for MoS2 flakes with different layers ranging from 1L to 11L. For each layer number of MoS2, at least five different samples were characterized in the statistical measurements. All the layer numbers were confirmed by AFM. (e) Intensity distribution pattern of the MoS2 micro-lens measured by scanning optical microscopy (SOM). (f) Intensity distribution pattern of the planar reference SiO2/Si substrate measured by the same SOM setup.
We used a far-field scanning optical microscopy (SOM) to characterize the fabricated MoS2 micro-lens (Supplementary Fig. S11). The SOM system used a green laser (at 532 nm) that was focused onto the focal plane of an Olympus 10X (NA = 0.25, depth of focus 18 μm) objective lens. The setup offered the best collection efficiency for light emitted from a small volume located around the focal plane. The micro-lens was moved along the z-axis in steps of 10 μm by a piezo-electrically driven stage. The camera recorded a series of the intensity distributions (Supplementary Fig. S12) with the MoS2 micro-lens positioned at different z values. A three-dimensional data set was generated by data processing and a cross-section profile was obtained along the x- and z-axes to illustrate the average distribution of the light intensity in these directions (Figure 3e). When the MoS2 micro-lens was placed at a distance 2|f| above the focal plane, the focused incident light would be exactly reimaged which is equivalent to the light coming from a point source (Supplementary Fig. S12d). Therefore, the camera recorded a well-focused light spot. The focal length f of the MoS2 micro-lens was measured to be –240 μm (2f= –480 μm), which matched very well with the simulated value (–248 μm) using the measured OPL profile of the micro-lens. For comparison, we also ran the same characterization by using a planar substrate without the MoS2 micro-lens, and obtained the intensity distribution shown in Figure 3f and Supplementary Fig. S13. The lensing effect is clearly demonstrated by comparing the difference between Figure 3e and 3f. In addition, the measured focal length of the MoS2 micro-lens shows weak polarization dependence (Supplementary Fig. S14), due to the low anisotropic dielectric response of MoS2. This makes MoS2 suitable for ultra-thin optical elements.
The efficiency of light scattering is another critical parameter for advanced light manipulation. Devices that employ photonic band gaps25, Anderson localization26, and light trapping such as with thin-film solar cells27all rely heavily on strong light scattering. Unfortunately, in typical 2D materials, such as graphene, the scattering efficiency is very small, making it impossible to rely on collective scattering of nanostructured graphene to achieve functionalities such as gratings. Here, we show that single- and few-layer structured MoS2 film have extraordinarily high scattering efficiency, enabled by the combination of high index in a thin structure. The scattering efficiency is determined by the strength of the electric field in the material. Normally, the electric field inside a bulk material, particularly a high-index material is much weaker than that of incident light because of the impedance mismatch. The boundary condition of Maxwell’s equations requires the tangential component of the electric field to be continuous across any interface. Because the layer is thin, this condition indicates that the electrical field inside a 2D material is almost as strong as the tangential component of the incident field. As a result, there is a strong polarization p = ɛ0 (n2 – 1)E0, where E0 is the electric field of s-polarized incident light, n is the index of the material and ɛ0 is the electric permittivity of free space. The scattering power is proportional to the p2 and, therefore, scales roughly as n2. This scaling rule greatly favors high-index materials and is again uniquely available in ultra-thin materials. In contrast, for nanoparticles, the scattering power is proportional to  , which does not increase appreciably with the refractive index28.
, which does not increase appreciably with the refractive index28.
Here we use the finite element method to explicitly calculate the scattering efficiency of 2D ribbons by solving Maxwell’s equations. Figure 4a shows the calculated scattering cross-section of an infinitely long ribbon (30 nm wide and 0.67 nm thick) in air for s-polarized light at normal incidence. The scattering cross-section has units of nanometers because the length of the ribbon is considered infinite. The scattering cross-section increases by orders of magnitude when the index increases by just a few times (Figure 4a). For example, the scattering cross-section of a single-layer MoS2 ribbon is around 670 times, 54 times, and 18 times of those in 0.67 nm SiO2, a single-layer graphene, and 0.67 nm of gold, respectively. Metal is generally considered as one of the strongest scattering materials and it is important to note that MoS2 even displays much stronger light scattering than gold. Moreover, the angular response of the scattering cross-section is also isotropic (Supplementary Fig. S15). Such favorable scaling for high-index materials is uniquely available in ultra-thin materials. The giant scattering efficiency in high-index 2D materials makes it possible to achieve sophisticated light manipulation based on collective scattering by patterns of nanostructures. Next, we experimentally demonstrate efficient optical gratings made from only a few layers of atoms. Because of the giant scattering efficiency, the efficiency of MoS2 gratings is orders of magnitude greater than those made from conventional materials, such as SiO2 and gold, and other low-index 2D materials.
Atomically thin high-efficiency gratings made from a single- and a few-layers of MoS2. (a) Simulated scattering cross-section (SCS) versus refractive index for a layer of 0.67 nm thick material. The SCS values of 0.67 nm Au, 0.67 nm SiO2, 1L (0.34 nm) graphene, and 1L (0.67 nm) MoS2 are represented by markers. The dashed line from equation y = 0.000167 x4 is added as a reference. (b) Schematic of the setup of the grating and for measurement of its diffraction efficiency. (c and d) Optical microscope images of 1L and 2L, and 8L MoS2 gratings. (e and f) AFM images of 1L and 2L, and 8L MoS2 gratings. Note: based on the measured grating height, the 1L, 2L, and 8L MoS2 were fully etched through and the SiO2 substrates underneath were over etched by around 1.5 nm. From our control SiO2 grating experiments and from simulations, the grating contribution from this over etched SiO2 is negligible. (g) Simulated and measured efficiency of an 8L MoS2 grating versus incident angle of the light beam. (h) The comparison of the simulated and measured maximum grating efficiencies for different materials. The dash line represents the noise level of our light detection system, with the minimum detectable grating efficiency being 0.02%.
We used FIB to mill grating patterns on 1L, 2L, 6L, and 8L MoS2 flakes (Figure 4 and Supplementary Fig. S16, S17, and S18). Grating parameters used in experiments, such as the periodicity and filling ratio, were based on optimal configuration predicted by simulations (Supplementary Table S1). The gratings were characterized using an s-polarized green laser (at a wavelength of 532 nm). The laser beam has a diameter of around 200 μm, which was large enough to fully cover the grating. First-order and second-order diffraction beams were observed and the measured diffraction angles agreed with the predictions of the diffraction equation d(sin θd + sin θi) = mλ, where θd and θi are the diffraction angle and incident angle, respectively; d is the period of the grating elements; and m is an integer characterizing the diffraction order. The power of the first-order diffraction beam was measured and the grating efficiency η was determined by η = (Pd/Pi) * (Sb/Sg), where Pd and Pi were the measured powers of the diffracted and incident beams, respectively; Sb and Sg were the measured areas of the incident beam and the MoS2 grating, respectively. The measured grating efficiency is a function of the incident angle, which agrees well with our simulation (Figure 4g). The maximum grating efficiencies for the 1L, 2L, 6L, and 8L MoS2 gratings were measured to be 0.3%, 0.8%, 4.4%, and 10.1%, respectively, which also agree well with the simulations (Figure 4h, Supplementary Table S1). For comparison, we also fabricated a grating from a graphene sheet deposited by large-area chemical vapor deposition (Supplementary Fig. S19a and S19b). The intensity of diffracted beam from the graphene grating was lower than the noise level of our light detection system, and thus had a maximum efficiency no greater than 0.02%. From our simulations, the maximum grating efficiency of mono-layer graphene would be only 0.0078%, which is around 47 times lower than that of a single-layer MoS2 grating. As another comparison, a SiO2 grating with 2 nm thickness was also fabricated (Supplementary Fig. S19c and S19d). Again no diffracted beam could be observed from the SiO2 grating due to the low grating efficiency in accordance with our numerical predictions (Figure 4h, Supplementary Table S1).
The efficiency of the MoS2 grating can be further improved by using a metallic mirror to replace the Si substrate. Based on simulations of optimized designs, the first-order grating efficiency of an 8L MoS2 grating can be up to 23.7% (Supplementary Table S2, Supplementary Fig. S20 and S21). In addition, an asymmetrical profile as used in high-efficiency gratings is expected to further improve the efficiency.
Conclusions
In conclusion, we have shown that high-index 2D materials have extraordinary elastic interactions with light, enabled uniquely by the ultra-thin nature of 2D materials. As a result, wavefront shaping29,30 and efficient light scattering can be accomplished with atomically thin 2D materials, enabling a new class of optical components entirely based on high-index 2D materials. Moreover, compared to conventional diffractive optical components, the spatial resolution of phase-front shaping is much smaller than the wavelength, and is only limited by the nano-fabrication resolution, making it possible to eliminate undesired diffraction orders30 2D materials also offer many unique advantages. Firstly, the extremely uniform thickness and the prefect surfaces with atomic roughness in layered high-index 2D materials provide us fantastic ways to precisely control the phase front of a wave. Secondly, the unique and large tunability of the refractive index by electric field31 in layered MoS2 will enable various applications in electrically tunable atomically thin optical components, such as micro-lenses with electrically tunable focal lengths, electrical tunable phase shifters with ultra-high accuracy, which cannot be realized by conventional bulk solids. Thirdly, we also observed similar giant OPL in other TMD family YX2 (Y=Mo, W; X=S, Se, Te) semiconductors, such as WS2 and WSe2 (Supplementary Fig. S22). The availability of different functional materials offers rich opportunities for the combination of optical and electronic properties, such as stacked atomically thin heterostructures for 2D optoelectronics. Fourthly, high-quality 2D TMD semiconductors can be deposited directly onto (or transferred to) various substrates with large size by chemical vapor deposition at low-cost32, potentially enabling low-cost flexible optical components. Lastly, quasi-2D optical components represents a significant advantage in manufacturing compared to conventional 3D optical components because different functionalities can all be achieved in a 2D platform sharing the same fabrication processes and this will greatly facilitate the large-scale manufacturing and integration. In summary, our work here opens an exciting opportunity to use high-index 2D materials to control the flow of light.
Author contributions
Y R L and Z F Y designed the project; J Y, R J X, and S Z carried out sample mechanical exfoliation and microscope imaging; J Y carried out the OPL, Raman, and PL measurements, AFM imaging, grating and micro-lens fabrication, grating efficiency measurement, and micro-lens characterization, with partial assistance from Y R L; Z W and Z F Y conducted the simulations and grating/micro-lens designs; F W and C J built the optical characterization setup for gratings and micro-lens. B L-D set up the PSI measurement system and provided technical support for the OPL characterization. J T and Q H Q undertook data processing for the micro-lens images. All authors contributed to the manuscript.
Competing financial interests
The authors declare that they have no competing financial interests.
References
Weiner J, Ho P-T . Light-matter Interaction, Fundamentals and Applications, Vol. 1. John Wiley & Sons, Inc .; 2003.
Engheta N, Ziolkowski RW . Metamaterials: Physics and Engineering Explorations. Wiley-IEEE Press; 2006.
Joannopoulos JD, Johnson SG, Winn JN, Meade RD . Photonic Crystals: Molding the Flow of Light, 2nd edn. Princeton and Oxford: Princeton University Press; 2008.
Bonaccorso F, Sun Z, Hasan T, Ferrari AC . Graphene photonics and optoelectronics. Nat Photonics 2010; 4: 611–622.
Lee SH, Choi M, Kim T-T, Lee S, Liu M et al. Switching terahertz waves with gate-controlled active graphenemetamaterials. Nat Mater 2012; 11: 936–941.
Ju L, Geng BS, Horng J, Girit C, Martin M et al. Graphene plasmonics for tunable terahertz metamaterials. Nat Nanotechnol 2011; 6: 630–634.
Vakil A, Engheta N . Transformation optics using graphene. Science 2011; 332: 1291–1294.
Lopez-Sanchez O, Lembke D, Kayci M, Radenovic A, Kis A . Ultrasensitive photodetectors based on monolayer MoS2 . Nat Nanotechnol 2013; 8: 497–501.
Liu CH, Chang YC, Norris TB, Zhong ZH . Graphenephotodetectors with ultra-broadband and high responsivity at room temperature. Nat Nanotechnol 2014; 9: 273–278.
Sundaram RS, Engel M, Lombardo A, Krupke R, Ferrari AC et al. Electroluminescence in single layer MoS2 . Nano Lett 2013; 13: 1416–1421.
Splendiani A, Sun L, Zhang YB, Li TS, Kim J et al. Emerging photoluminescence in monolayer MoS2 . Nano Lett 2010; 10: 1271–1275.
Wang SX, Yu HH, Zhang HJ, Wang AZ, Zhao MW et al. Broadband few-layer MoS2 saturable absorbers. Adv Mater 2014; 26: 3538–3544.
Yin XB, Ye ZL, Chenet DA, Ye Y, O’Brien K et al. Edge nonlinear optics on a MoS2 atomic monolayer. Science 2014; 344: 488–490.
Zeng HL, Dai JF, Yao W, Xiao D, Cui XD . Valley polarization in MoS2 monolayers by optical pumping. Nat Nanotechnol 2012; 7: 490–493.
Mak KF, He KL, Shan J, Heinz TF . Control of valley polarization in monolayer MoS2 by optical helicity. Nat Nanotechnol 2012; 7: 494–498.
Zhang S, Yang J, Xu RJ, Wang F, Li WF et al. Extraordinary photoluminescence and strong temperature/angle-dependent Raman responses in few-layer phosphorene. ACS Nano 2014; 8: 9590–9596.
Yang J, Xu RJ, Pei JJ, Myint YW, Wang F et al. Optical tuning of exciton and trion emissions in monolayer phosphorene. Light Sci Appl 2015; 4: e312; doi:10.1038/lsa.2015.85.
Yang J, Lü TY, Myint YW, Pei JJ, Macdonald D et al. Robust excitons and trions in monolayer MoTe2 . ACS Nano 2015; 9: 6603–6609.
Xu RJ, Yang J, Zhu Y, Yan H, Pei JJ et al. Layer-dependent surface potential of phosphorene and anisotropic/layer-dependent charge transfer in phosphorene-gold hybrid systems. Nanoscale 2016; 8: 129-135.
Wang QH, Kalantar-Zadeh K, Kis A, Coleman JN, Strano MS . Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat Nanotechnol 2012; 7: 699–712.
Radisavljevic B, Radenovic A, Brivio J, Giacometti V, Kis A . Single-layer MoS2 transistors. Nat Nanotechnol 2011; 6: 147–150.
Xu XD, Yao W, Xiao D, Heinz TF . Spin and pseudospins in layered transition metal dichalcogenides. Nat Phys 2014; 10: 343–350.
Zhang H, Ma YG, Wan Y, Rong X, Xie Z et al. Measuring the refractive index of highly crystalline monolayer MoS2 with high confidence. Sci Rep 2015; 5: 8440.
Blake P, Hill EW, Castro Neto AH, Novoselov KS, Jiang D et al. Making graphene visible. Appl Phys Lett 2007; 91: 063124.
Yablonovitch E . Inhibited spontaneous emission in solid-state physics and electronics. Phys Rev Lett 1987; 58: 2059–2062.
John S . Strong localization of photons in certain disordered dielectric superlattices. Phys Rev Lett 1987; 58: 2486–2489.
Yu ZF, Raman A, Fan SH . Thermodynamic upper bound on broadband light coupling with photonic structures. Phys Rev Lett 2012; 109: 173901.
Jackson JD . Classical Electrodynamics, 3rd edn. John Wiley & Sons Ltd .; 1998.
Lin D, Fan P, Hasman E, Brongersma ML . Dielectric gradient metasurface optical elements. Science 2014; 345: 298–302.
Yu NF, Capasso F . Flat optics with designer metasurfaces. Nat Mater 2014; 13: 139–150.
Santos EJG, Kaxiras E . Electrically driven tuning of the dielectric constant in MoS2 layers. ACS Nano 2013; 7: 10741–10746.
van der Zande AM, Huang PY, Chenet DA, Berkelbach TC, You YM et al. Grains and grain boundaries in highly crystalline monolayer molybdenum disulphide. Nat Mater 2013; 12: 554–561.
Acknowledgements
We would like to acknowledge support from the ACT node of the Australian National Fabrication Facility (ANFF) and, particularly, the technical support on the FIB provided by Dr Li (Lily) Li. We also thank Professor Jin-cheng Zheng, from Xiamen University (China), for helpful discussions, and Professor Vincent Craig and A/Professor Lan Fu, from the Australian National University, for support on AFM and optical imaging. We acknowledge the financial support from an ANU PhD scholarship;the Office of Naval Research (USA) under grant number N00014-14-1-0300;the Australian Research Council (grant number DE140100805); and the ANU Major Equipment Committee.
Note: Accepted article preview online 18 November 2015
Author information
Authors and Affiliations
Corresponding authors
Additional information
Note: Supplementary Information for this article can be found on the Light: Science & Applications' website.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 Unported License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission fromthe license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Yang, J., Wang, Z., Wang, F. et al. Atomically thin optical lenses and gratings. Light Sci Appl 5, e16046 (2016). https://doi.org/10.1038/lsa.2016.46
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2016.46
Keywords
This article is cited by
-
Ultra-sensitive nanometric flat laser prints for binocular stereoscopic image
Nature Communications (2021)
-
π-phase modulated monolayer supercritical lens
Nature Communications (2021)
-
Metalenses go atomically thick and tunable
Nature Photonics (2020)
-
Exciton resonance tuning of an atomically thin lens
Nature Photonics (2020)
-
Nanoscale plasmonic phase sensor
Analytical and Bioanalytical Chemistry (2020)